【状态估计】观测信号（包括异常值）的状态估计方法（Matlab代码实现）

?💥💥💞💞欢迎来到本博客????💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

??座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 测试1

2.2 测试2

🎉3?参考文献

🌈4 Matlab代码、数据、文章

---

💥1 概述

文献来源：

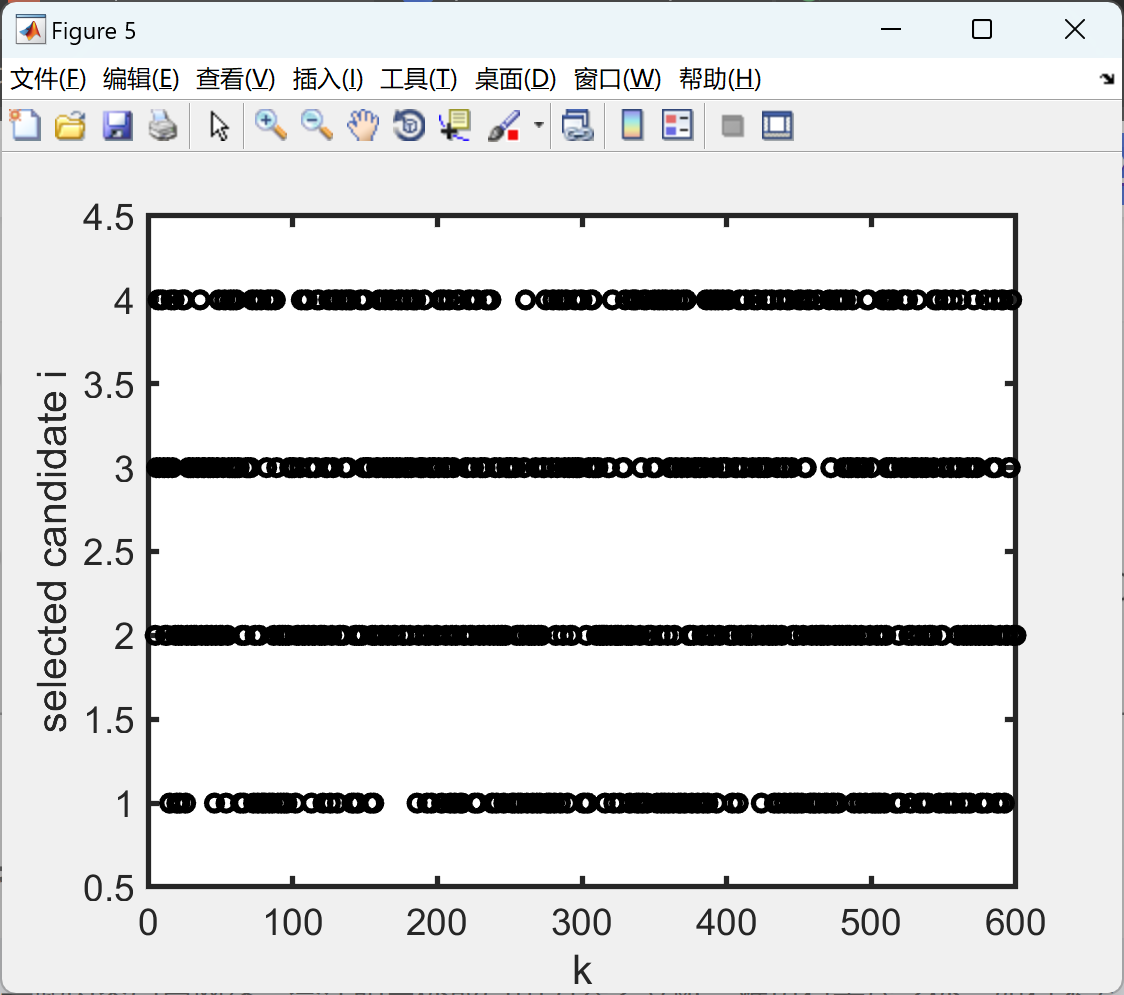
本文讨论了观测输出包含离群值的系统的状态估计问题。当观测输出存在离群值时，状态估计的准确性会明显下降。为了克服这一问题，提出了一种使用多个估计状态候选者的新型观测器结构。首先，创建了多个估计状态的候选者；每个候选者使用不同检测时机的传感输出数值。如果离群值出现不太频繁，消除受离群值影响的候选者可以防止估计准确性的恶化。我们提出的观测器使用中值或加权中值操作从获得的估计状态候选者中选择一个。通过中值操作，从这些候选者中选择不使用离群值的估计状态。此外，还提供了一种基于估计状态误差的可达集合，利用基于李雅普诺夫不等式设计这些估计状态候选者的观测器增益的方法。通过数值例子说明了所提出的观测器的有效性。

在控制工程中，状态反馈控制是控制系统中最重要的方法之一。在状态反馈控制中，计算每个时间点所有状态值加权的总和，并将计算得到的值作为输入信号应用到控制系统中。一般来说，使用传感器测量所有状态值是困难的；因此，在控制系统的实施中也使用状态观测器[Citation1–6]。状态观测器是一个系统，它从实际系统的输入和测量输出中提供给定实际系统内部状态的估计。它在各种情况下被使用，比如当传感器无法使用或者由于成本问题不能观测到所有内部状态时。

通过将植物模型包括在状态观测器中，可以通过使用输入u和输出y的信息来寻求内部状态x的估计状态xf。尽管状态观测器已经研究了很长时间，但最近几年涉及状态观测器的各种研究领域取得了进展，比如车辆运动控制系统[Citation8,Citation9]、网络控制[Citation10]系统和网络控制系统。状态观测器和使用卡尔曼滤波器的状态估计技术可以应用于线性和非线性系统的情况[Citation4]。对植物状态量的适当估计在控制系统设计中起着重要作用。已经开发了各种状态观测器设计方法以实现令人满意的估计性能[Citation15–17]。

一般来说，当使用状态观测器时，假定存在噪声和干扰。已知当与离群值[Citation11–14,Citation19]和数据包丢失[Citation21–23]相关的问题出现时，估计准确性会显著下降。在使用非接触传感器（如视觉传感器）的情况下，有时可能会出现离群值。由于亮度急剧变化的影响、移动障碍物导致的通信阻塞等。

📚2 运行结果

2.1 测试1

2.2 测试2

测试结果图比较多，就不一一展示。

部分代码：

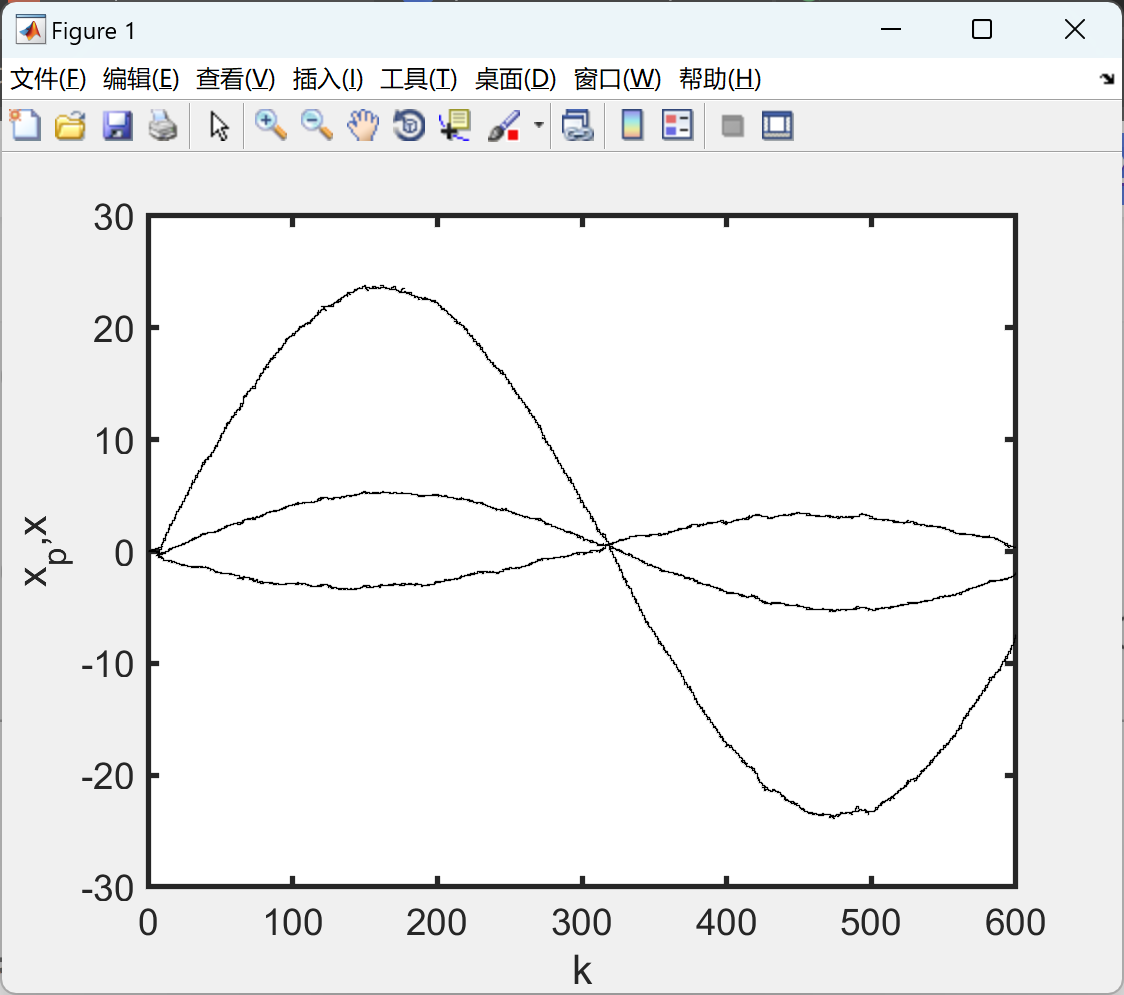
figure(1),stairs(t,xa(1,:),'k','LineStyle','--','LineWidth',2),hold on,stairs(t,xa(2,:),'k','LineStyle','--','LineWidth',2),hold on,stairs(t,xa(3,:),'k','LineStyle','--','LineWidth',2)
figure(1),stairs(t,xtotal(1,:),'r'),hold on,stairs(t,xtotal(2,:),'r'),hold on,stairs(t,xtotal(3,:),'r'),axis([0 600 -30 30]);
%figure(2),stairs(t,x2(1,:),'b'), hold on
%figure(3),stairs(t,x3(1,:),'k'), hold on
%figure(4),stairs(t,xtotal(1,:),'k'), hold on

ylabel('x_p,x')
xlabel('k')

ya(1,601) = 0;
ya(2,601) = 0;

figure(2)
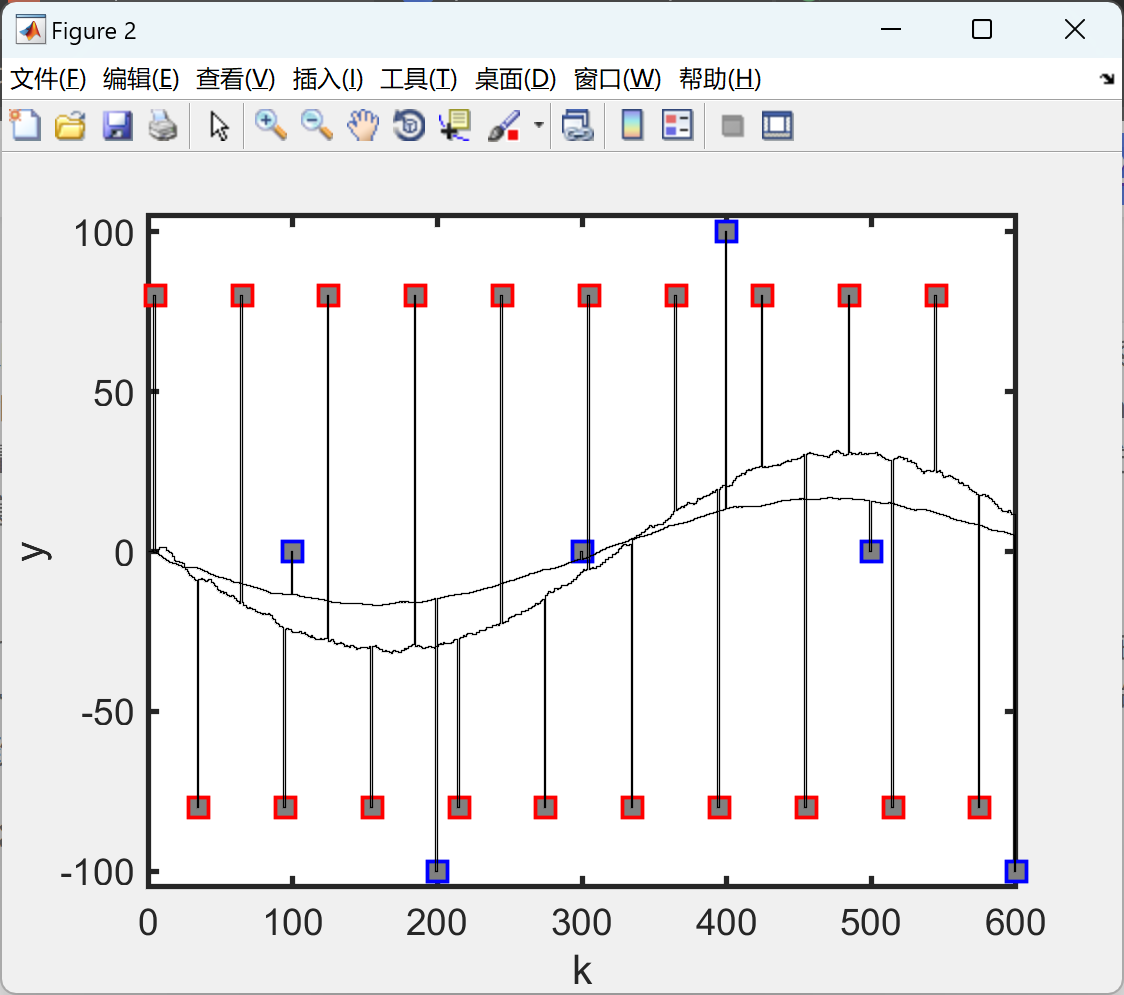
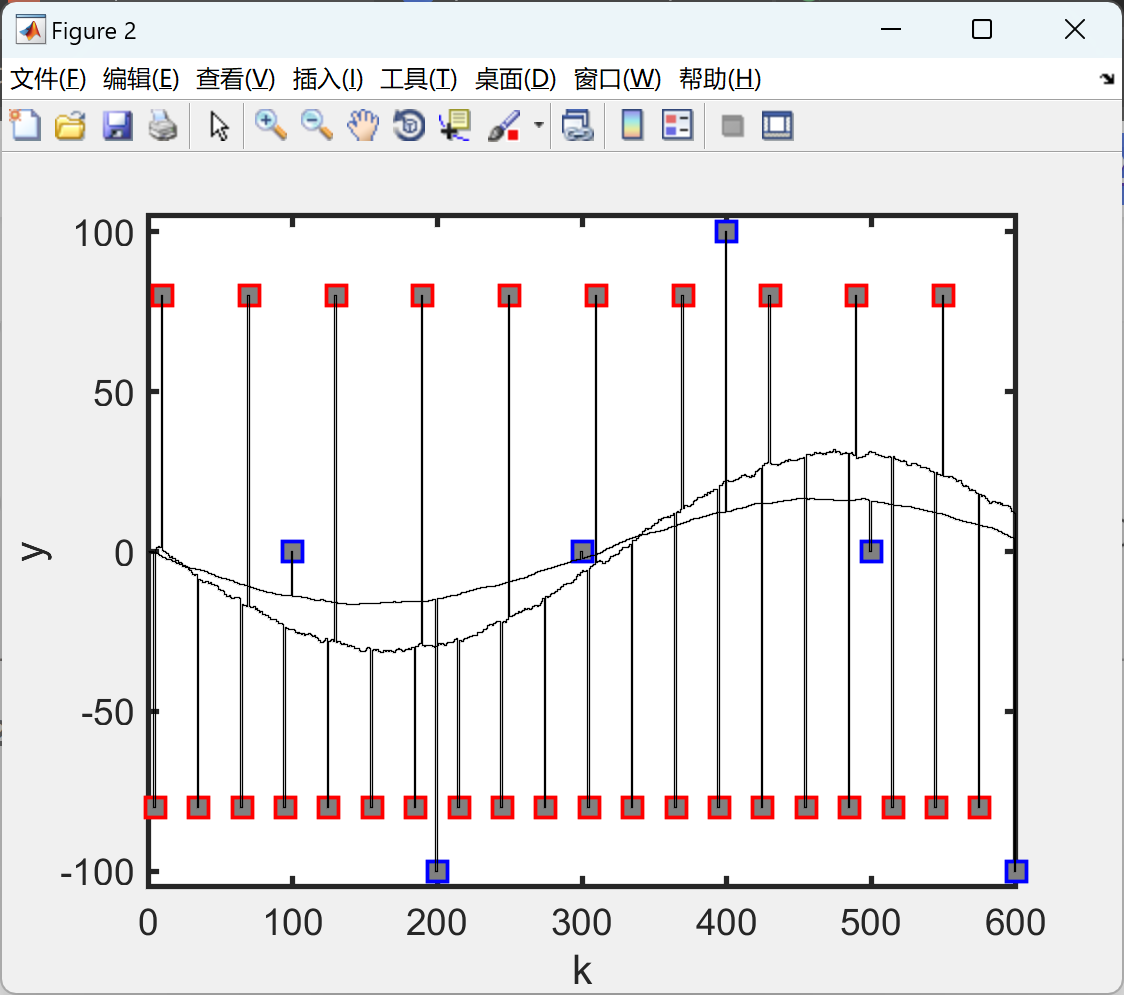
stairs(t,ya(1,:),'k')
hold on,axis([0 600 -105 105]);
stairs(t,ya(2,:),'k'),axis([0 600 -105 105]);
hold on

ylabel('y')
xlabel('k')

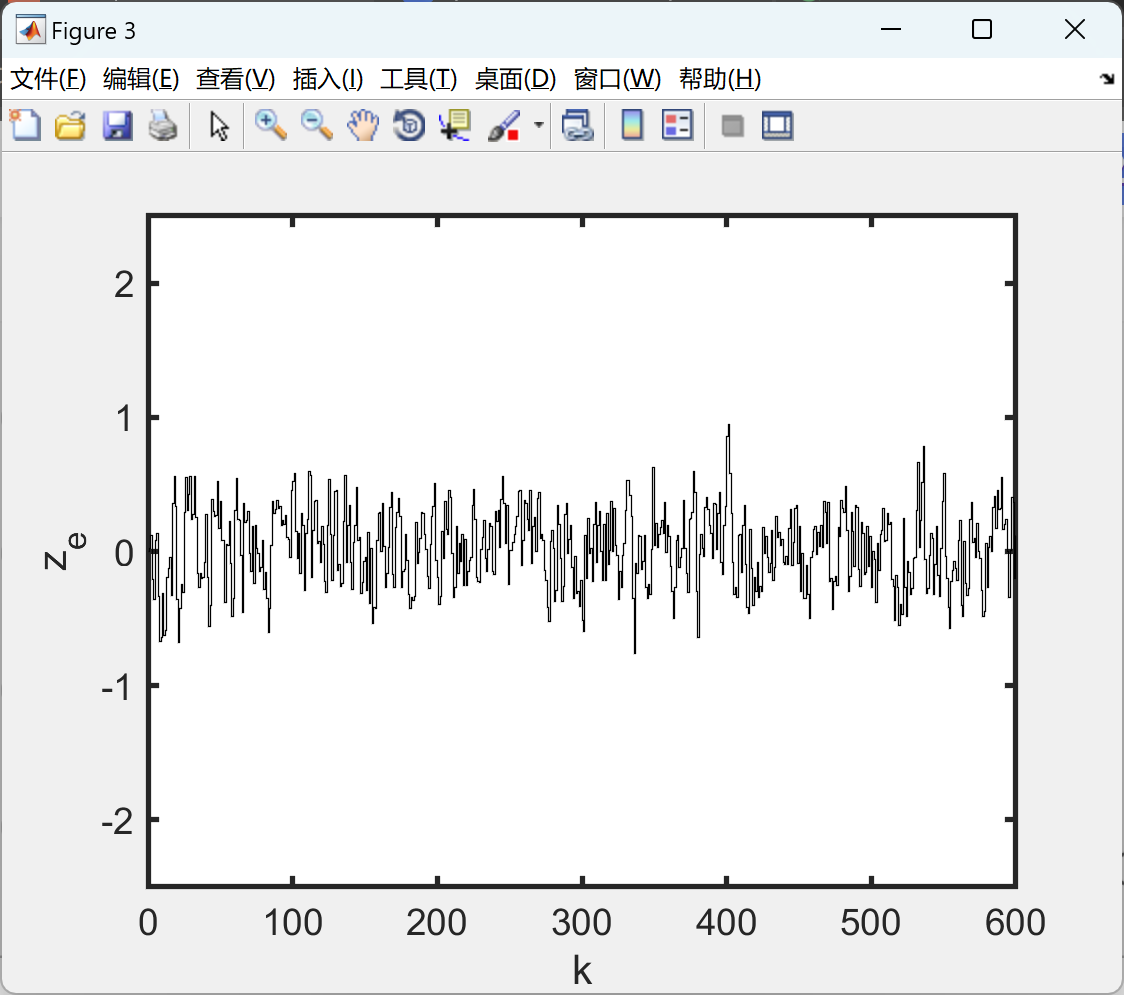
figure(3) %z,zQ1
stairs(t,E(1)*(xa(1,:)-xtotal(1,:))+E(2)*(xa(2,:)-xtotal(2,:))+E(3)*(xa(3,:)-xtotal(3,:)),'k','LineWidth',0.5);
axis([0 600 -2.5 2.5])
%set(gca,'fontsize',14);
xlabel('k')
ylabel('z_e')

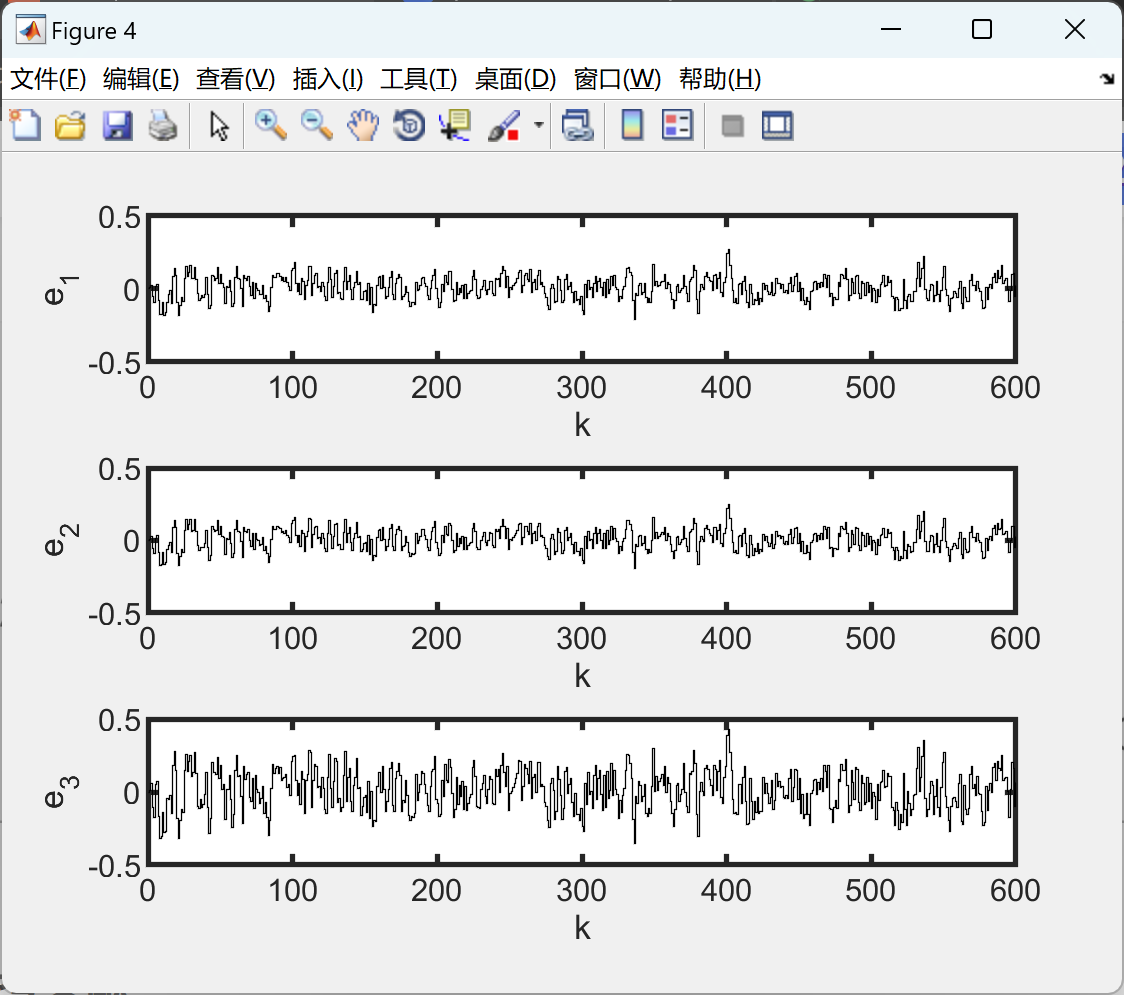
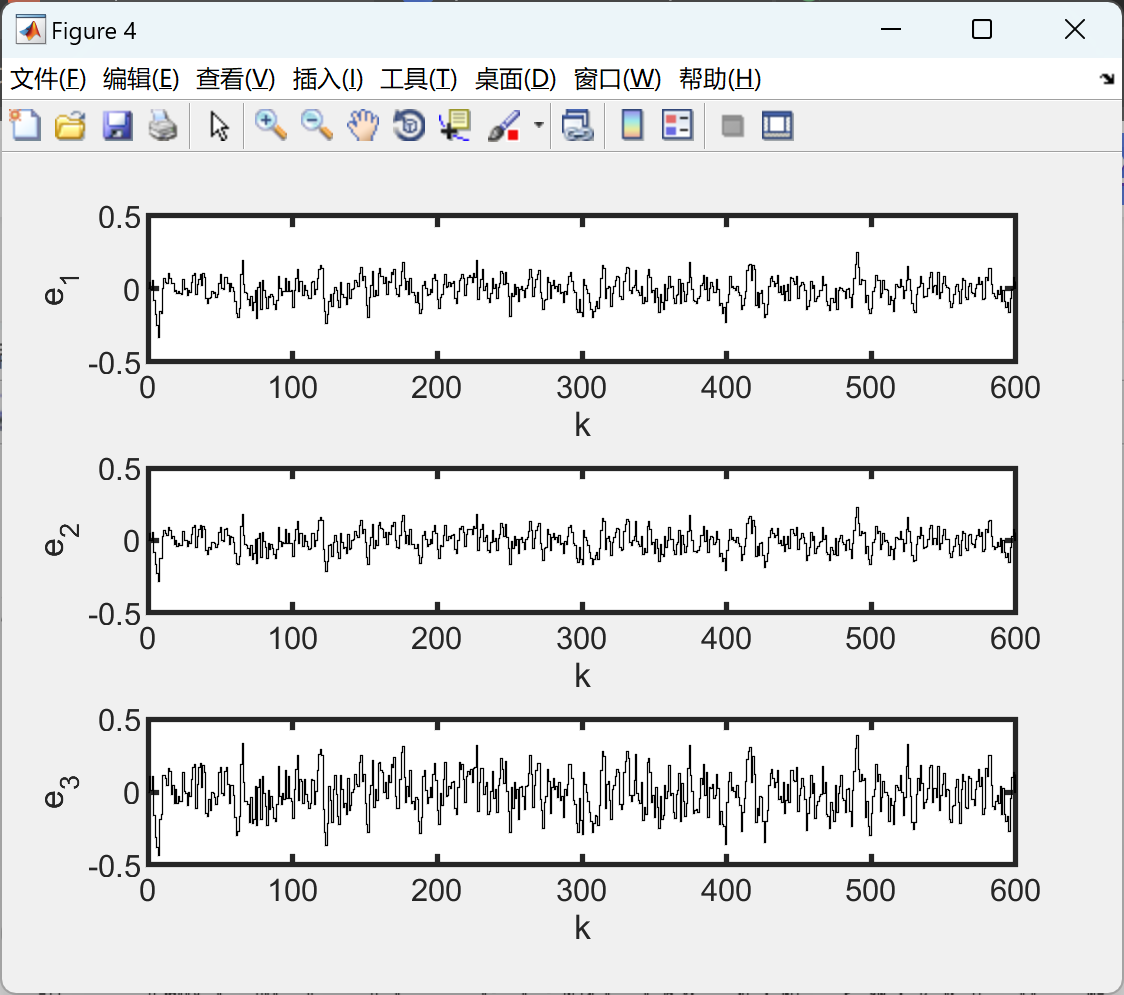
figure(4) %z,zQ1
subplot(3,1,1)
stairs(t,(xa(1,:)-xtotal(1,:)),'k','LineWidth',0.5);
axis([0 600 -.5 .5])
ylabel('e_{1}')
xlabel('k')
%set(gca,'fontsize',14);
subplot(3,1,2)
stairs(t,xa(2,:)-xtotal(2,:),'k','LineWidth',0.5);
axis([0 600 -.5 .5])
%set(gca,'fontsize',14);
ylabel('e_{2}')
xlabel('k')
subplot(3,1,3)
stairs(t,xa(3,:)-xtotal(3,:),'k','LineWidth',0.5);
axis([0 600 -.5 .5])
%set(gca,'fontsize',14);
ylabel('e_{3}')
xlabel('k')

🎉3?参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文章