不同数据类型在内存中的存储（浮点数）

前言

环境（vs2022,x64）浮点数的存储

当初学习C语言的时候，很多人可能并不会深入关注浮点数的存储方式。刚开始可能更专注于理解基础的语法和计算机组成的一般概念。听到关于浮点数可能影响精度的说法时，可能并不容易理解。?然而，在学习计算机组成的过程中，涉及到浮点数的计算时，了解浮点数的存储方式就变得非常重要。浮点数的存储涉及到底层的二进制表示、尾数、指数等概念，这对于理解计算机如何处理小数和进行浮点数运算至关重要。虽然刚开始可能觉得这些细节并不直接影响编程，但随着对计算机体系结构的深入理解，你会发现浮点数的存储方式对于避免精度问题、理解数值范围、以及正确处理浮点数运算都起着关键作用。因此，在学习C语言和计算机组成时，逐渐深入了解浮点数的存储方式是值得投入时间的重要一步。

浮点数的基本概念

浮点数是一种用于表示带小数部分的数值的数据类型。它与整数不同，可以表示范围更广泛的实数，包括小数和大数。以下是浮点数的基本概念：

1. 符号位：浮点数的第一位是符号位，用于表示正数或负数。0表示正数，1表示负数。

2. 尾数（Mantissa）：尾数是浮点数的小数部分，它由二进制小数表示。在IEEE 754标准中，尾数总是以规格化形式表示，即以1.xxxxx...的形式，其中1是尾数的隐含位，后面是小数部分。

3.指数：?指数用来表示浮点数的阶码，指数部分通常采用二进制表示。指数影响浮点数的大小范围，通过它可以调整小数点的位置，实现表示大范围的数。

4. 规格化形式：浮点数的规格化形式是指尾数总是以1.xxxxx...的形式表示，这样可以更有效地存储小数部分，并确保在表示非常小或非常大的数时能够保持较好的精度。

5. 阶码的偏移（Bias）：为了方便表示负指数，IEEE 754标准引入了偏移值（bias），它在指数部分加上一个固定值，通常为127，来达到表示负指数的目的。

综合这些概念，浮点数的二进制表示形式可以由符号位、指数和尾数组成，采用规格化形式确保了有效的小数表示。了解这些基本概念有助于理解浮点数在计算机中的存储方式和运算规则。

看这些概念并不容易理解，举个浮点数转化成16进制和二进制的例子，有些浮点数是无法被完整表示成二进制的，因为他的小数点部分是有权值的，比如第一位是0.5，第二位是0.25，以此类推，比如，3.14的尾数，就无法被完整表示，他是无限循环的，我们只能储存在23位数的限制下的近似值，这就导致，浮点数在表示某些小数的时候，会出现精度缺失的问题，我们也可以在编译器中尝试，99.99就无法被完整的存储在内存中，这就是浮点数可能影响精度的原因。

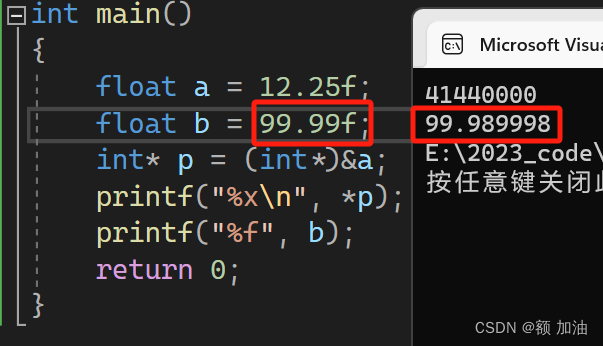
那么，我就用12.25这个浮点数，按照浮点数的存储方式，来计算他在内存中的16进制存储的数值。首先，将 12.25 转换为单精度浮点数的二进制表示。 12?的二进制表示为 1100，而 0.25的二进制表示为 0.01。

将整数部分和小数部分合并，得到 12.25?的二进制表示为 1100.01。

接下来，根据IEEE 754单精度浮点数的存储结构：

符号位（1 bit）：0（表示正数）

阶码部分（8 bits）：由于指数是正数，需要加上偏移量127。实际的指数值是 3，二进制表示为 10000010。指针数值是按照，1.xxxx *2^n? n就是实际指数值，就是将这个二进制转化成二进制的科学表示法（类似我们小学学的十进制的科学表示法）偏移量是默认加上的，由于指数有可能为负数，但是IEEE754规定，该数为无符号数，阶码为8位，也就是什么数加上这个偏移量，都是正数，也就是无符号数

尾数部分（23 bits）：整数部分和小数部分合并，即 10001000000000000000000。在IEEE754标准下，因为是二进制表示，无论是正数还是负数，当他们转化成科学表示法后，第一位都是 1 为了更加精准表示浮点数，就省略这一位 1 将后面23位都用来表示后面的尾数

将这三部分组合起来，得到 12.25的单精度浮点数的二进制表示：

0?10000010?10001000000000000000000

将这个二进制串转换为十六进制：

0x41440000?

所以，12.25?在单精度浮点数中的十六进制表示为 0x41440000。我们可以用编译器来验证这个结果

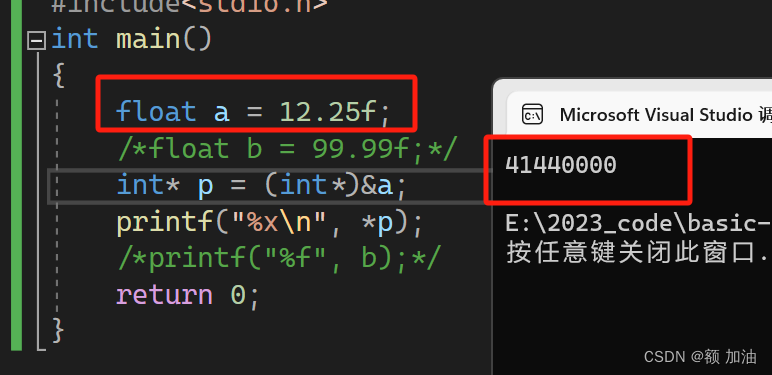
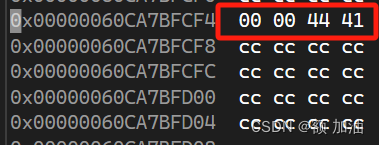
我们同样可以在调试内存中看到这个结果，但是为什么是从右边到左边这就涉及到机器存储的另外一个知识?字节序（Big Endian 或 Little Endian）也就是大段存储和小段存储?

Endian表示的意思是（多字节数据类型（如整数或浮点数）的存储中，字节的顺序）

Big Endian（大端序）： 在大端序中，最高有效字节（MSB）存储在最低内存地址处，而最低有效字节（LSB）存储在最高内存地址处。即，数据的高位字节存储在较低的内存地址，而低位字节存储在较高的内存地址。

Little Endian（小端序）： 在小端序中，最低有效字节（LSB）存储在最低内存地址处，而最高有效字节（MSB）存储在最高内存地址处。即，数据的低位字节存储在较低的内存地址，而高位字节存储在较高的内存地址。

让我们仔细看上面那张图片，从左到右，地址增加，（我们可以把内存监视器列改为1来查看每一个比特位的地址的高低）我们数据的高位段也在高地址处，也就是说，我运行程序的环境下（vs2022），是小端存储

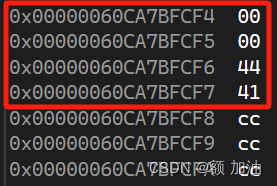，那这些存储在内存中的ccccccccccc是什么呢？

那就要涉及到函数开辟空间时，编译器的定义了，如果有朋友想要了解，可以留言，我会写篇介绍他的内容。