力扣309. 买卖股票的最佳时机含冷冻期（动态规划，Java C++解法）

Problem: 309. 买卖股票的最佳时机含冷冻期

题目描述

思路

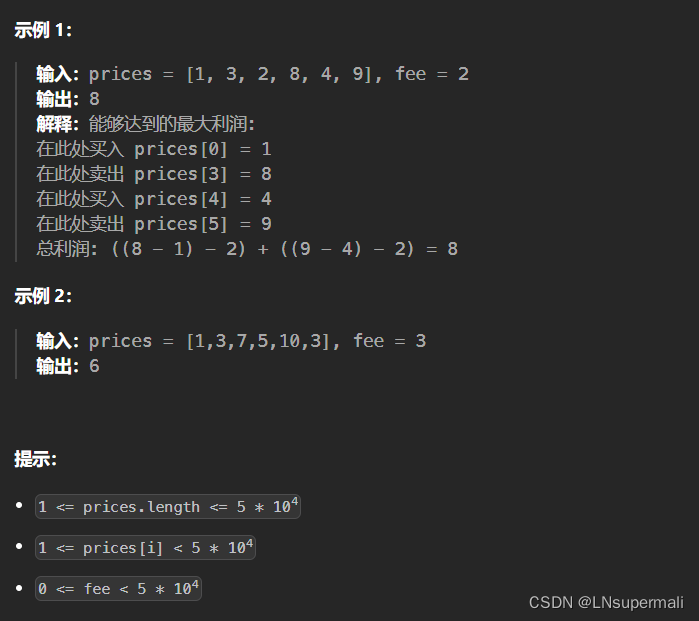
Problem: 714. 买卖股票的最佳时机含手续费
该题目可以看作是上述题目的改编，该题目添加了一个冷冻期使得动态转移方程更加复杂，具体思路如下：
1.构建多阶段决策模型：

n天对应n个阶段，每个阶段决策：买股票、卖股票、不操作
买股票：前一天不持有股票，并且处于冷冻期或者处于非冷冻期，而不是刚刚昨天卖掉股票
卖股票：当前持有股票
不操作无规则

2.定义状态：每天都有两种状态：持有股票、不持有股票。不持有股票又分为三小种情况。

int dp[n][4]表示n天的状态
dp[i][0]表示第i天持有股票时的利润
dp[i][1]表示第i天不持有股票时的利润（当天卖掉）
dp[i][2]表示第i天不持有股票时的利润（冷冻期），昨天刚卖掉了股票
dp[i][1]表示第i天不持有股票时的利润（非冷冻期），昨天也没持有

3.定义状态转移方程：

dp[i][0] = max3(dp[i - 1][0], dp[i - 1][2] - prices[i], dp[i - 1][3] - prices[i]);
dp[i][1] = dp[i - 1][0] + prices[i];
dp[i][2] = dp[i - 1][1];
dp[i][3] = Math.max(dp[i - 1][2], dp[i - 1][3]);

解题方法

1.获取prices数组的长度(假设为n)，定义数组int[][] dp = new int[n][4];
2.初始化dp数组的第一行：dp[0][0] = -prices[0];dp[0][1] = 0;dp[0][2] = 0;dp[0][3] = 0;
3.从第一行开始完成动态转移方程；
4.返回dp数组的最后一行的最大值

复杂度

时间复杂度:

$O(n)$；其中$n$为数组prices的大小

空间复杂度:

$O(n)$

Code

class Solution {
   /**
     * Dynamic programming
     * @param prices Given array(Recode the amount of each stock)
     * @return int
     */
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if (n == 1) {
            return 0;
        }
        int[][] dp = new int[n][4];
        /**
         * dp[i][0] represents the profit from holding the stock on day i
         * dp[i][1] represents the profit not held on day i (just sold on the day)
         * dp[i][2] represents the profit from not holding the stock on day i (the freeze period),
         * which was sold yesterday
         * dp[i][3] represents the profit from not holding the stock on day i
         * (non-freezing period) and not holding it yesterday
         */
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        dp[0][2] = 0;
        dp[0][3] = 0;
        //Dynamic transfer
        for (int i = 1; i < n; ++i) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][2] - prices[i], dp[i - 1][3] - prices[i]);
            dp[i][1] = dp[i - 1][0] + prices[i];
            dp[i][2] = dp[i - 1][1];
            dp[i][3] = Math.max(dp[i - 1][2], dp[i - 1][3]);
        }
        return max(dp[n - 1][0], dp[n - 1][1], dp[n - 1][2], dp[n - 1][3]);
    }

    /**
     * Returns the largest number in a set of numbers
     * @param nums Given numbers 
     * @return int
     */
    private int max(int... nums) {
        int max = Integer.MIN_VALUE;
        for (int num : nums) {
            if (num > max) {
                max = num;
            }
        }
        return max;
    }
}

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n == 1) {
            return 0;
        }
        vector<vector<int>> dp(n, vector<int>(4));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        dp[0][2] = 0;
        dp[0][3] = 0;
        for (int i = 1; i < n; ++i) {
            dp[i][0] = ::std::max(dp[i - 1][0], ::std::max(dp[i - 1][2] - prices[i], dp[i - 1][3] - prices[i]));
            dp[i][1] = dp[i - 1][0] + prices[i];
            dp[i][2] = dp[i - 1][1];
            dp[i][3] = ::std::max(dp[i - 1][2], dp[i - 1][3]);
        }
        return ::std::max({dp[n - 1][0], dp[n - 1][1], dp[n - 1][2], dp[n - 1][3]});
    }
};