【每日一题】2397. 被列覆盖的最多行数-2024.1.4

题目：

2397. 被列覆盖的最多行数

给你一个下标从?0?开始、大小为?m x n?的二进制矩阵?matrix?；另给你一个整数?numSelect，表示你必须从?matrix?中选择的?不同?列的数量。

如果一行中所有的?1?都被你选中的列所覆盖，则认为这一行被?覆盖?了。

形式上，假设?s = {c1, c2, ...., cnumSelect}?是你选择的列的集合。对于矩阵中的某一行?row?，如果满足下述条件，则认为这一行被集合?s?覆盖：

• 对于满足?matrix[row][col] == 1?的每个单元格?matrix[row][col]（0 <= col <= n - 1），col?均存在于?s?中，或者
• row?中?不存在?值为?1?的单元格。

你需要从矩阵中选出?numSelect?个列，使集合覆盖的行数最大化。

返回一个整数，表示可以由?numSelect?列构成的集合?覆盖?的?最大行数?。

示例 1：

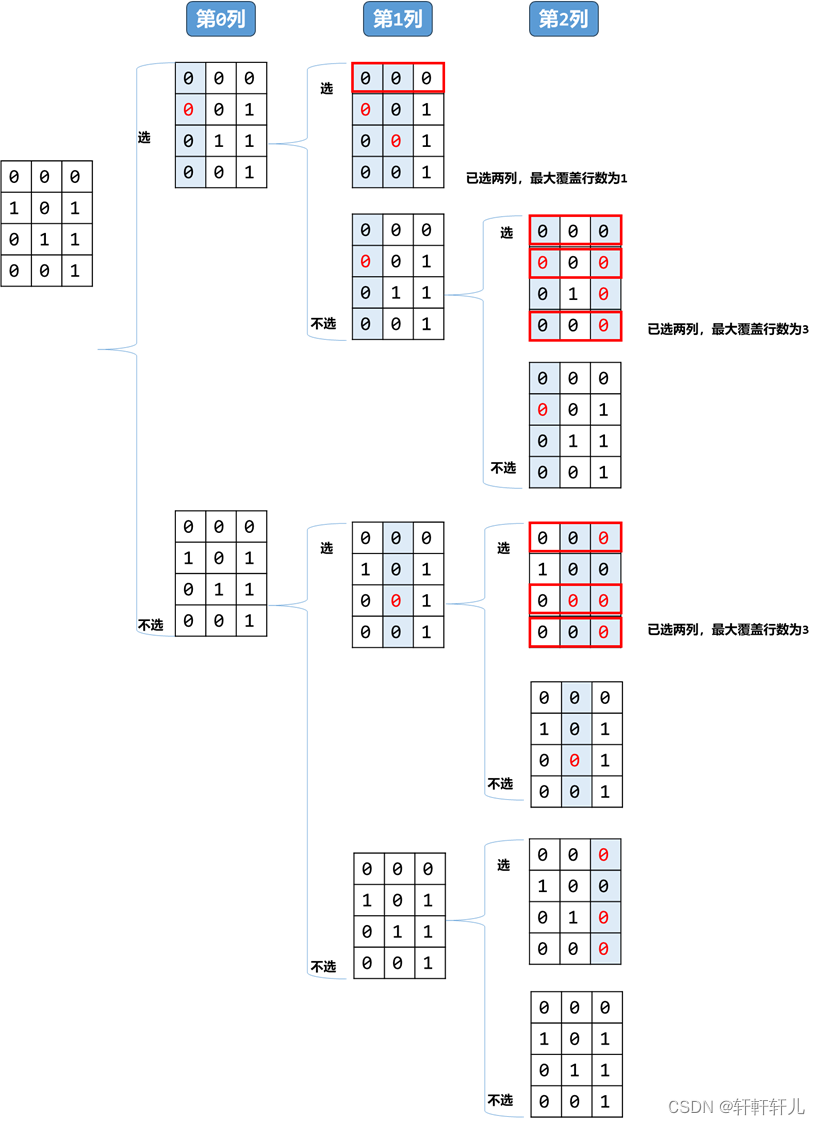
输入：matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出：3
解释：
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖，因为其中没有出现 1 。
- 第 1 行被覆盖，因为值为 1 的两列（即 0 和 2）均存在于 s 中。
- 第 2 行未被覆盖，因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖，因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此，可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行，但可以证明无法覆盖更多行。

示例 2：

输入：matrix = [[1],[0]], numSelect = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，因为整个矩阵都被覆盖了。
所以我们返回 2 。

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 12
• matrix[i][j]?要么是?0?要么是?1
• 1 <= numSelect?<= n

解答：

代码：

class Solution {
    private int maxRows=0;//覆盖最大行数，初始为0
    public int maximumRows(int[][] matrix, int numSelect) {
        int m=matrix.length;
        int n=matrix[0].length;
        int[] masks=new int[m];//存储每一行的数字掩码
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                masks[i]|=(matrix[i][j]<<j);//生成每一行的数字掩码，将第j个数字添加到mask从右往左的第j位
            }
        }
        backtracking(masks,numSelect,n,0,0);//回溯枚举所有的列选择集合，统计覆盖最大行数
        return maxRows;
    }
    /**
     * 对当前idx列有选与不选两种选择
     * @param masks: 每一行的数字掩码
     * @param numSelect: 当前还可以选择的列数
     * @param n: 总列数，也是列索引上界
     * @param idx：当前处理的列索引
     * @param s: 选择的列集合掩码
    */
    private void backtracking(int[] masks,int numSelect,int n,int idx,int s){
        if(numSelect==0){
            int coverRows=0;//统计当前s可以覆盖的行数
            for(int mask:masks){
                //mask & ~s如果选择的列在改行为1，置为0
                //如果结果为0，说明当前行所有列都为0，该行被覆盖，行数+1；否则该行未被覆盖，行数+0
                coverRows+=1-Math.min(1,mask&~s);
            }
            maxRows=Math.max(maxRows,coverRows);//可以选择的列数为0，更新最大覆盖行数
            return;
        }
        if(idx==n) return;//列索引到达上界
        backtracking(masks,numSelect,n,idx+1,s);//不选当前列，直接递归
        s|=(1<<idx);//选择当前列，将当前列在s中的对应位置1
        backtracking(masks,numSelect-1,n,idx+1,s);//选择当前列后，递归处理
    }
}

结果：