代码随想录算法训练营第四十二天|01背包问题、01背包问题(滚动数组)、416. 分割等和子集
发布时间:2024年01月23日
题目:01背包问题
文章链接:代码随想录
视频链接:LeetCode:背包问题
题目链接:卡码题目链接
图释:

//二维dp数组实现
#include <bits/stdc++.h>
using namespace std;
int n, bagweight;// bagweight代表行李箱空间
void solve() {
vector<int> weight(n, 0); // 存储每件物品所占空间
vector<int> value(n, 0); // 存储每件物品价值
for(int i = 0; i < n; ++i) {
cin >> weight[i];
}
for(int j = 0; j < n; ++j) {
cin >> value[j];
}
// dp数组, dp[i][j]代表行李箱空间为j的情况下,从下标为[0, i]的物品里面任意取,能达到的最大价值
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化, 因为需要用到dp[i - 1]的值
// j < weight[0]已在上方被初始化为0 dp[i][0] 表示背包重量为0,怎么取都是装不下的
// j >= weight[0]的值就初始化为value[0]
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
// 如果装不下这个物品,那么就继承dp[i - 1][j]的值
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
// 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值
// 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
while(cin >> n >> bagweight) {
solve();
}
return 0;
}题目:01背包问题(滚动数组)
文章链接:代码随想录
视频链接:LeetCode:背包问题(滚动数组)
题目链接:卡码网题目链接
图释:

// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;
int main() {
// 读取 M 和 N
int M, N;
cin >> M >> N;
vector<int> costs(M);
vector<int> values(M);
for (int i = 0; i < M; i++) {
cin >> costs[i];
}
for (int j = 0; j < M; j++) {
cin >> values[j];
}
// 创建一个动态规划数组dp,初始值为0
vector<int> dp(N + 1, 0);
// 外层循环遍历每个类型的研究材料
for (int i = 0; i < M; ++i) {
// 内层循环从 N 空间逐渐减少到当前研究材料所占空间
for (int j = N; j >= costs[i]; --j) {
// 考虑当前研究材料选择和不选择的情况,选择最大值
dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
}
}
// 输出dp[N],即在给定 N 行李空间可以携带的研究材料最大价值
cout << dp[N] << endl;
return 0;
}题目:416. 分割等和子集
文章链接:代码随想录
视频链接:LeetCode:416.分割等和子集
题目链接:力扣题目链接
图释:
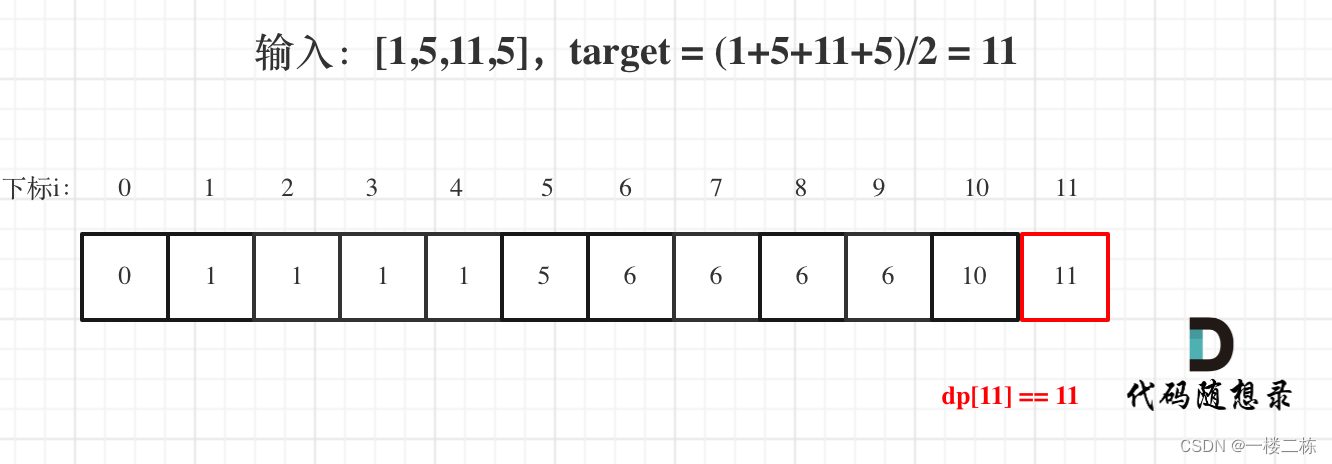
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
// dp[j] 表示容量为j的背包,最多能装dp[j]价值的东西
vector<int> dp(10001, 0); //初始化为其他数时,会影响滚动数组max(dp[i],...)的值
for(int i=0; i<nums.size(); i++){
sum += nums[i];
}
if(sum % 2==1) return false; // 不能被2整除,则无法得到两个元素和相等的子集
int target = sum / 2;
for(int i=0; i<nums.size(); i++){ // 遍历物品,背包中只取一次nums[i]
for(int j=target; j>=nums[i]; j--){
// 相当于背包的最大容量为目标值target, 背包要大于物品重量,物品重量大于背包负重则结束循环
dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]); //此时的dp[j]表示还未放入nums[i]的最大值
}
}
// 如果背包刚好能装满,则说明能分割为两个元素和相等的子集
if(dp[target]==target) return true;
return false;
}
};
文章来源:https://blog.csdn.net/m0_71413464/article/details/135766554
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!