【数据结构】四、串

目录

一、定义

二、表示与实现

定长顺序存储

堆分配存储

链式存储

三、BF算法

四、KMP算法

1.求next数组

方法一

方法二（考试方法）

2.KMP算法实现

方法一

方法二

3.nextval

4.时间复杂度?

---

本节最重要的就是KMP算法，其他要求不高

一、定义

串类型的定义：串即字符串，是由零个或多个字符组成的有限序列，是数据元素为单个字符的特殊线性表。

串长：串中字符的个数（n≥0)，n=0 时称为空串?

空白串：由一个或多个空格符组成的串，空串不等于空白串

子串：串S中任意个连续的字符序列叫S的子串，?S叫主串（空串是任意串的子串；任意串S都是S本身的子串，除S本身外，S的其他子串称为S的真子串）

子串位置：子串的第一个字符在主串中的序号

字符位置：字符在串中的序号

串相等：串长度相等，且对应位置上字符相等

下面关于串的的叙述中,哪一个是不正确的?

A. 串是字符的有限序列

B.?空串是由空格构成的串

C.?模式匹配是串的一种重要运算

D.?串既可以采用顺序存储,也可以采用链式存储

答案：B?

二、表示与实现

定长顺序存储

用预先设定好长度的数组存储串。string[MAXSIZE + 1]，加一是为了给串尾的‘\0’留空间

堆分配存储

也就是用malloc动态创建数组，还可以用realloc增加空间

链式存储

用链表存储串值，易插入和删除

1.链表结点的数据域长度取1

2.链表结点数据域长度取n（块链结构）

当数据元素较多时，块链结构存储密度更高

三、BF算法

BF算法是一种串的模式匹配算法，目的是确定主串中所含子串第一次出现的位置

思路：

主串S，模式串T

将ST的头部对齐，逐个比较字符是否相同

一旦出现不同，将T后移一位，重新从头开始比较

直到完全匹配为止，否则匹配失败

写成代码：

主串S，模式串T【i，j为S，T的指针】

将ST的头部对齐【i，j分别指向S，J的首位】，逐个比较字符是否相同【S[i]==T[j]】

一旦出现不同【S[i] != T[j]】，将T后移一位【i = i - j + 2（回溯）】，重新从头开始比较【j指向T首位】

直到完全匹配为止【j > T的长度】，否则匹配失败【i > S的长度】

时间复杂度：最坏情况为：主串n长，子串m长；除了最后一次，每一次都比较到子串最后一位发现不匹配，总共比较?m*(n-m+1)+m?次。时间复杂度 O(n*m)

四、KMP算法

改进BF算法：当字符不匹配时，利用已匹配部分的信息，仅让模式串回溯，主串不回溯

模式串要回溯到什么地方呢？目标地点记录在next[ ]数组中

next数组是干什么的呢？next数组记录了已匹配部分最大相同前后缀的信息

比如

S = a b a c c a b a b

P = a b a b

开始匹配

S =?a b a c c a b a b

P = a b a b?

前三位都匹配，第四位b与c不匹配

此时我们知道已匹配的部分为a b a，它有相同的前后缀‘a’

我们只需要让T的“前缀”与S的“后缀”对齐，接着比较即可。主串不需要回溯，子串也不用从头开始

S = a b a c c a b a b

P =? ? ? ?a b a b

next数组是一个与模式串等长的数组，它告诉我们，模式串第几位失配时我们要跳转到哪里

所以关键在于求next数组

1.求next数组

方法一

方法二（考试方法）

假设next从j = 1开始编号

1）j = 1时，next[j] = 0

2）j > 1时，next[j] = j之前的最大相同前后缀长度 +1

3）j > 1时，找不到相同前后缀时，next[j] = 1

比如

方法二可以由方法一每位都加一得到，哪个舒服用哪个

2.KMP算法实现

方法一

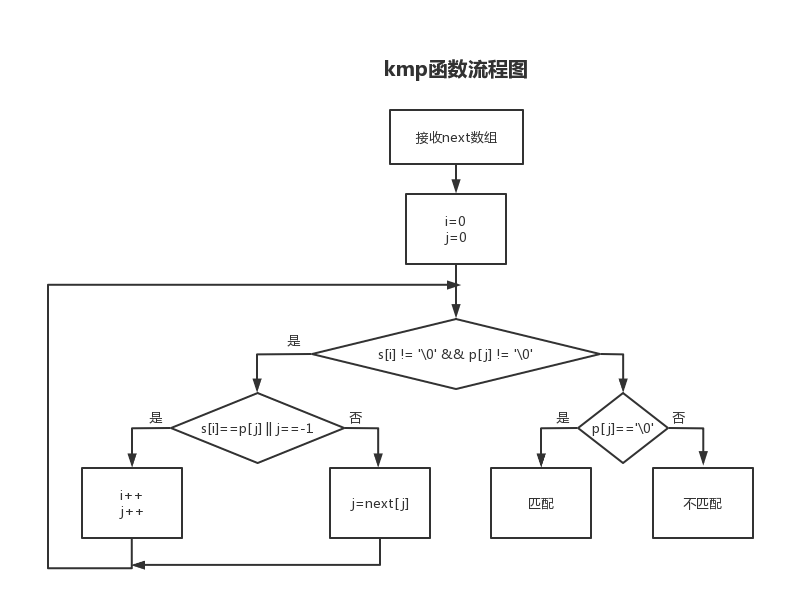
完整例子，找到一段话中的所有匹配：

// 在一篇英文文章中查找指定的模式串，采用KMP算法实现
 
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
 
#define elemtype char
 
elemtype* getnext(elemtype* p)  //传入模式串得到next数组
{ 
	int pnum = strlen(p);
	elemtype* next = (elemtype*)malloc(sizeof(elemtype) * pnum);
	next[0] = 0;
	int len = 0;
	int k = 1;
 
	//生成next数组
	while (p[k] != '\0') 
    {
		if (p[len] == p[k])
			next[k++] = ++len;
		else
			(len == 0 ? next[k++] = 0 : len = next[len - 1]);
	}
 
	//调整next数组
	for (k = pnum - 2; k >= 0; k--)   
		next[k + 1] = next[k];
	next[0] = -1;
 
	//输出next数组
	printf("next数组为：");
	for (k = 0; k < pnum; k++)       
		printf("%d ", next[k]);
	printf("\n");
	return next;
}
 
void kmp(elemtype* s, elemtype* p) //传入两个串
{   
 
	elemtype* next = getnext(p);
 
	int i = 0;
	int j = 0;
	int flag = 1;
 
	while (flag == 1) {
		while (s[i] != '\0' && p[j] != '\0') 
        {
			if (j == -1 || s[i] == p[j])
            {
				i++;
				j++;
			}
			else  j = next[j];
		}
 
		if (p[j] == '\0') 
        {
			printf("字符串在编号%d处与模式串匹配\n", i - j);
			j = 0;   //匹配后模式串从头开始，继续寻找匹配点
		}
		else flag = 0;  //当字符串遍历完后才退出
	}
}
 
int main() {
 
	elemtype s[] = "No Person shall be a Senator who shall not have attained to the Age of thirty Years, and been nine Years a Citizen of the United States, "
					" and who shall not, when elected, be an Inhabitant of that State for which he shall be chosen.";
	elemtype p[] = "shall";	
	printf("字符串为：%s\n", s);
	printf("模式串为：%s\n", p);
 
	kmp(s, p);
}

方法二

3.nextval

有模式串p，next数组

数组都是从1开始编号

nextval计算方法：

nextval[1] = 0

对于第i位，如果p[i] 不等于 p [ next [i] ] , nextval [i] = next [i]

? ? ? ? ? ? ? ? ? ?如果p [i] 等于 p [ next [i] ]，则 j = next [i]，继续比较p [j] = p [ next [j] ]，一直向前比较，直到不等或到首位为止

例一：?

字符串‘a b a b a a b a b’ 的next为：0 1 1 2 3 4 2 3 4；nextval为：0 1 0 1 0 4 1 0 1

例二：

求字符串‘a b c a a b b c a b c a a b d a b’的next和nextval

next：? ? ?0 1 1 1 2 2 3 1 1 2 3 4 5 6 7 1 2

nextval：0 1 1 0 2 1 3 1 0 1 1 0 2 1 7 0 1?

4.时间复杂度?

由于不用回溯，主串只走一遍，加上计算next时所用的比较次数m，为O(m+n)? BF为O(n*m)