浅谈 Java 数组链表

????????数组和链表是我们最常用也是最基本的数据结构，严格来说基础的数据结构就只有两种，就是数组和链表，其他的各种高阶的数据结构都是从数组和链表中衍生出来的，它们只是在不同的业务场景中根据数组或链表而衍生出来的解决方案。所以说数组和链表是一切数据结构的根本，我们完全有必要更深层次的理解这两种数据结构。如果你对数组和链表的理解仅仅还只限于 ”数组查询数据快插入删除数据慢，链表插入删除快查询数据慢” 这个层面的话，那么你完全有继续阅读这篇文章的必要。

数组

数组它是由相同类型的元素的集合所组成的一种线性数据结构，当我们创建一个数组时，在内存里面是分配了一块连续的内存空间来存储的，当我们获取数组中的元素时，可以通过元素的索引计算出该元素对应的存储地址。

总结来说数组的3个核心规则：

1、数组在内存里面是一块连续的内存空间。

2、数组里存的元素类型是相同的。

3、数组是通过索引来获取对应的元素。

1、数组的创建

  int[] numbers=new int[8]

在Java里面，当我们执行上面的代码的时候，就会在内存里面申请一个长度为5，数据类型为int的数组，它 在内存里面是以一段连续的内存空间来标识。

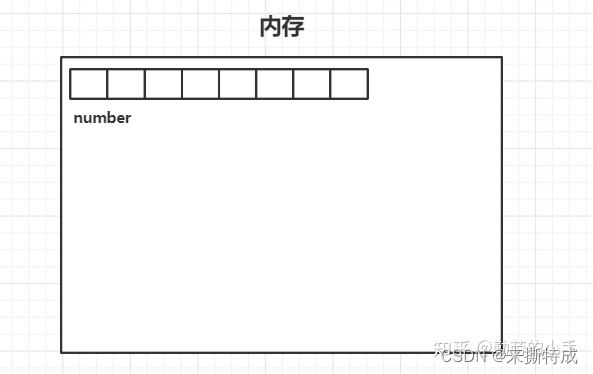
为什么必须指定数组的数据类型？

曾经我有一个问题，不知道你是否有同样的疑惑，就是为什么数组必须限定存储的是同一种类型的数据？其实如果你思考过一个问题，那么就能得出答案，思考一下如果我们在创建一个数组的时候不指定数据类型，那么意味着我是无法知道未来这个数组会存储什么数据的，如果在我不知道需要存储什么数据的情况下又如何知道我要向内存申请多大的空间来创建这个数组呢？显然这么一思考答案就不言而喻了。

好了，现在我们已经知道了数组在创建的时候就指定了能存储的数据类型了，那么创建数组的时候，只需要稍微计算一下就能知道需要向内存申请的空间大小了，比如new int[8] 我会向内存申请一个8*4 字节的大小的内存空间(int类型数据占用4字节)。

2、数组获取元素的过程。

知道了元素的数据类型，知道了内存空间是连续的，那我们肯定也能想到如何去根据索引去获取数组对应的元素了，比如说我获取number[2]的数据，那么我们只需要根据 下标位*数据占用的大小，这样计算就可以得到下标位为2的数据在内存中的位置了，当然真正的计算过程是通过下标位计算指针的偏移量的方式得到的，但逻辑上却是一样的，同时在申请数组的时候还会记录数组在内存开始标记位和结束标记位，通过开始标记位和结束标记位，然后通过索引加上数据类型的大小计算出偏移量就能读取到数组对应下标位的数据。

?

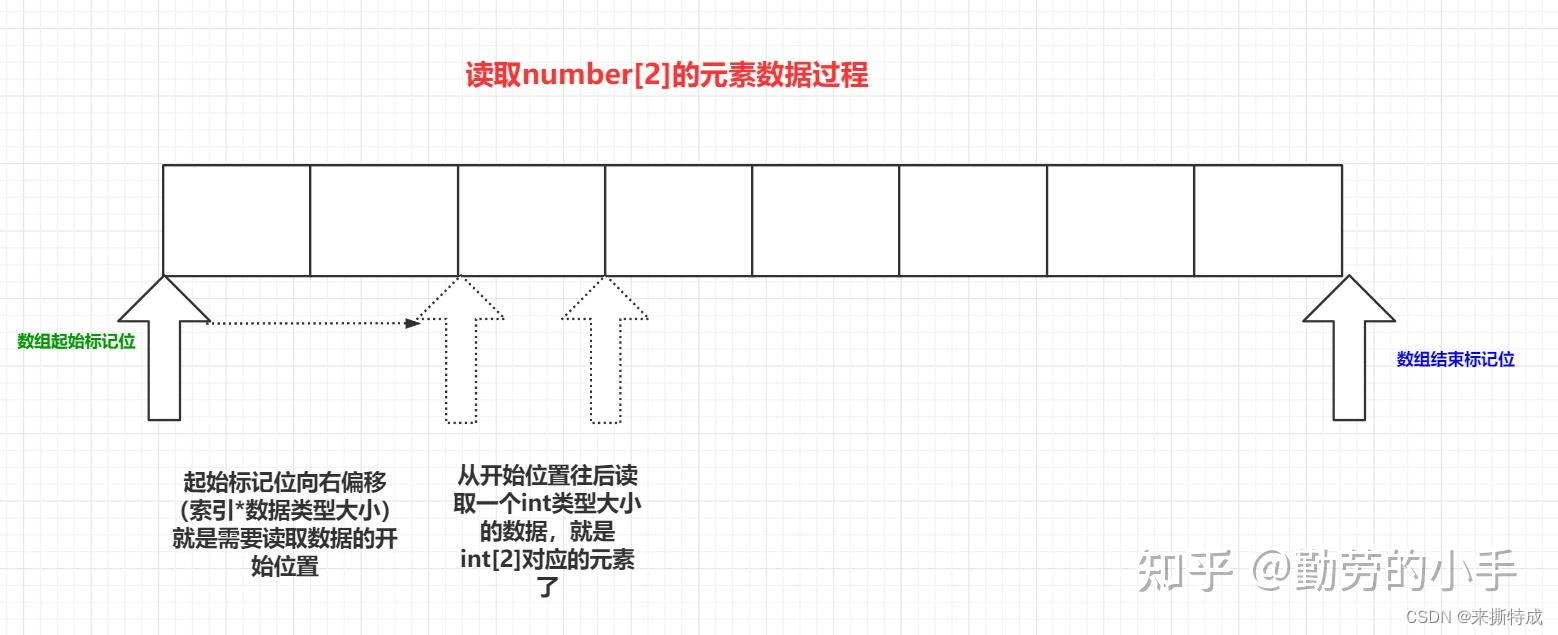
我们通过下标计算出指针偏移量，这样我们无论获取数组哪个下标位的数据都只要通过一次计算就能得到对应下标位的数据，这也是我们通常说数组的查询元素的时间复杂度为O(1)。

3、数组插入元素的过程。

查询数组元素的过程我们已经知道了，现在我们来看数组是如何插入和删除元素的，当然对数组有一定了解的对这个操作过程印象都会比较深，就是数组在删除或者添加某个元素时候都会有一个挪动后面元素的过程。

比如我们往下number[3] 的地方插入一个值333，那么整个过成就会是这样：我们得先把后续下标位置>=3的元素统一往后挪一位，当把下标为3位置的内存空间空余出来之后，然后才把333的值保存到数组下标为3的位置。

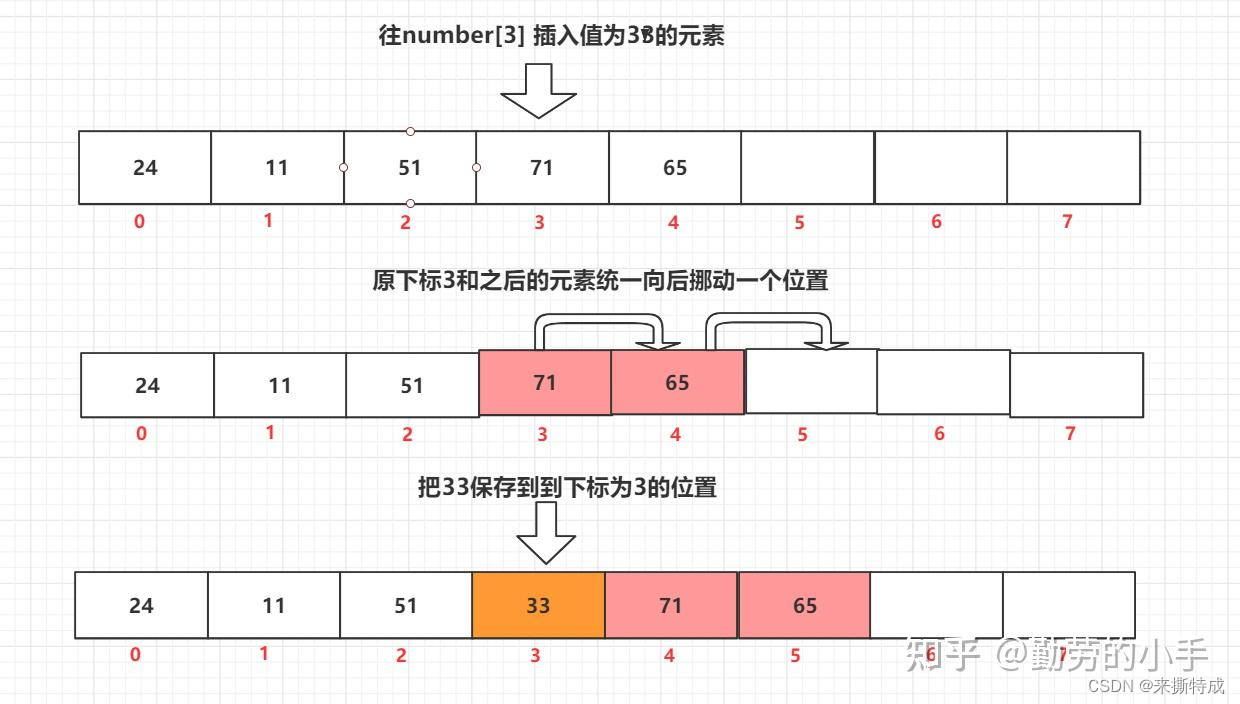
好奇心重的人也许对于这个过程会有一个疑问，为什么要把之后的元素全部都往后挪呢，可不可以只把原数组中下标为3的数据直接挪到最后位置，然后把新的数据放到下标3的位置就行了吗？这样不就省掉了一部分元素挪动的工作，是否可以提升一下数组插入数据的性能呢， 我觉得如果对于数据的原顺序性没什么要求的话，这也许会是一种优化。

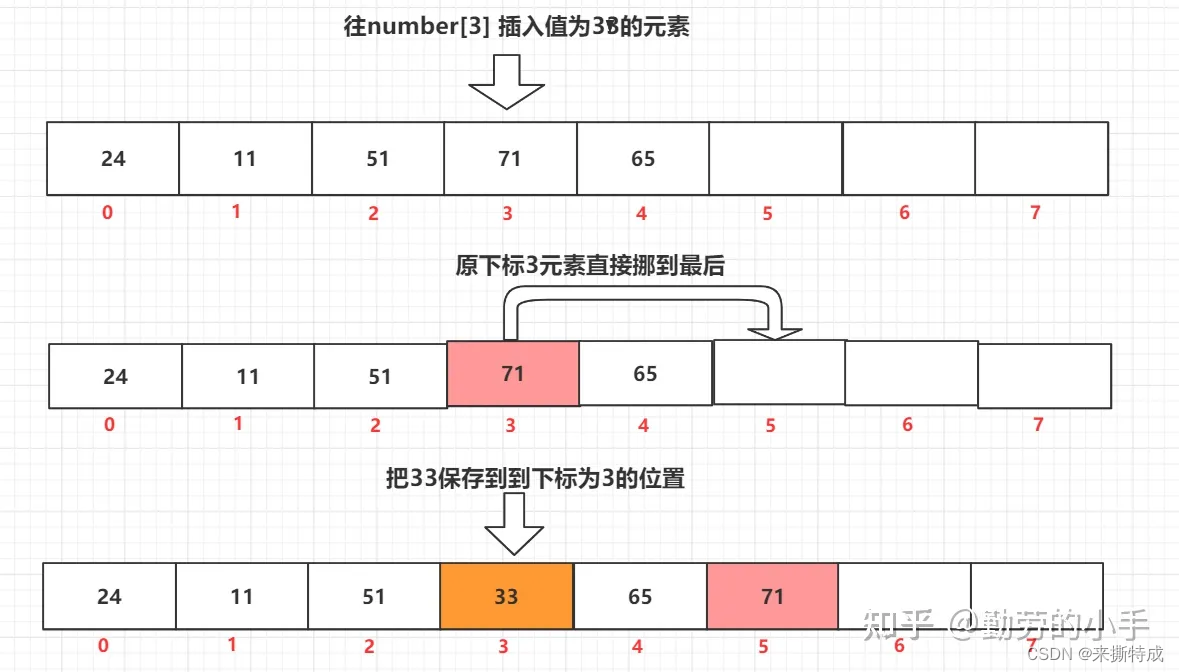
4、数组删除元素的过程。

数组删除和数组插入的逻辑差不多，既然往中间插入一个元素后面的就要集体往后挪，那么删除一个元素就自然而然把后面的元素往前挪咯，假如我们删除int[3]下标的元素，那么操作过程就会如下图。

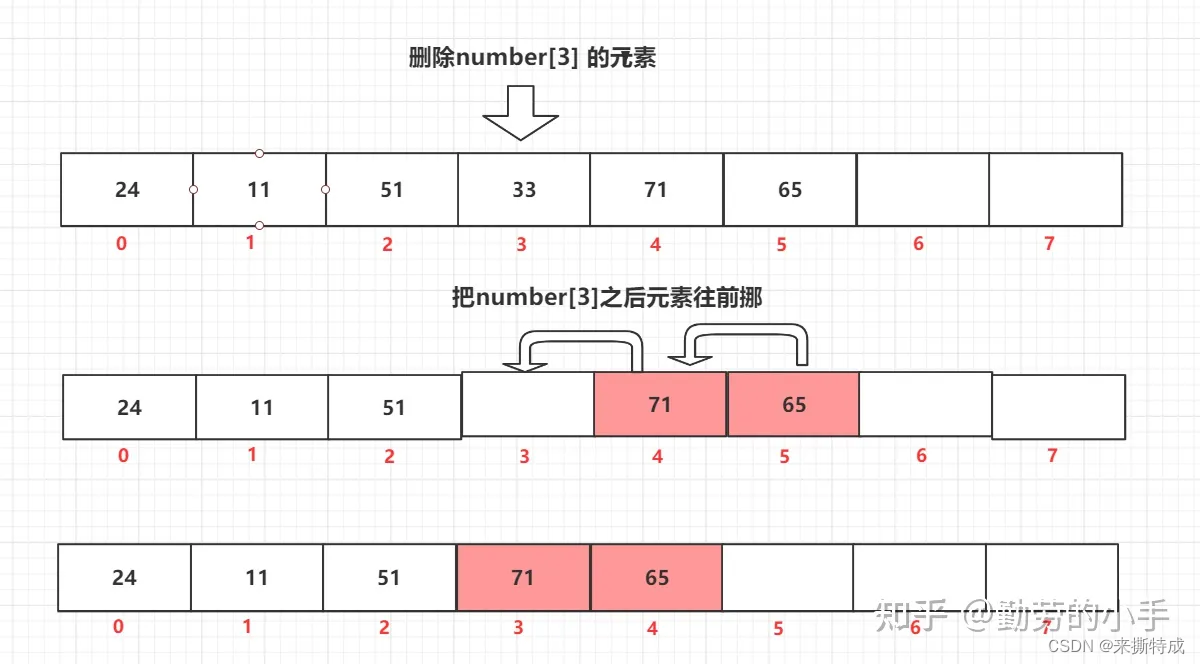
数组的删除和插入其挪动元素的逻辑差不多，插入的数据越靠前，那么需要做的挪动操作就越多，所以插入和删除元素的操作时间复杂度可以估算成0(n)的时间复杂度。

好的，到这里好奇的人又来了，这里是不是也可以像插入元素一样，直接把最后一个元素挪到int[3]位置就行了，又或者说我就干脆不挪了，直接删了不就得了，至于删除的位置直接空着就行了么。好像也有道理，也不会出什么大问题是吧，只是获取对应元素的时候为空就是了；前者和会打乱原来元素的排列顺序。后者好像并不是一个好的设计，这样会造成很多数组空间无法再次使用到，也就是我们常说的空间碎片。

不过还有一个想法倒是具有实践意义，就是删除的时候我先只标记，而不是真的马上删除对应的数据，等到积累到了一定的数量之后，我们再统一把标记删除了的数据进行删除，那么这样就省掉了频繁删除数据导致数组元素挪动的过程了，这个过程就有点像我们JVM进行垃圾收集的时候使用的标记整理法（先对删除的元素进行标记，到达一定数量统一清除，再对数组的元素进行整理）。

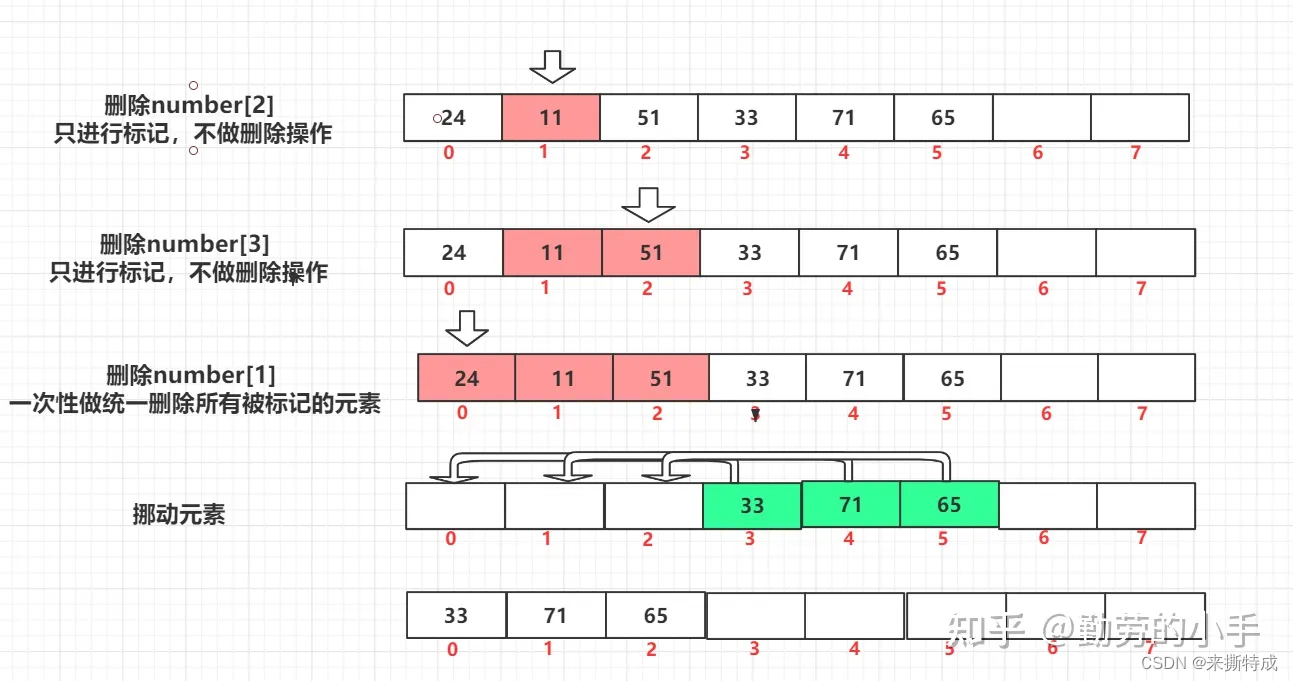
5、数组的扩容

因为数组内存连续性的要求，所以在申请内存的时候的时候必须指定申请的空间大小，而这个空间大小在申请后就已经固定无法变更，所以数组自己是没办法进行扩容的，只是我们人为用逻辑的方式对数组进行扩容，我们可以通过创建一个更大的新数组，然后把原数组的元素一个个迁移到新数组上来，通过这种方式进行人为的扩容，这些是我们常说的List，HashMap的扩容逻辑。

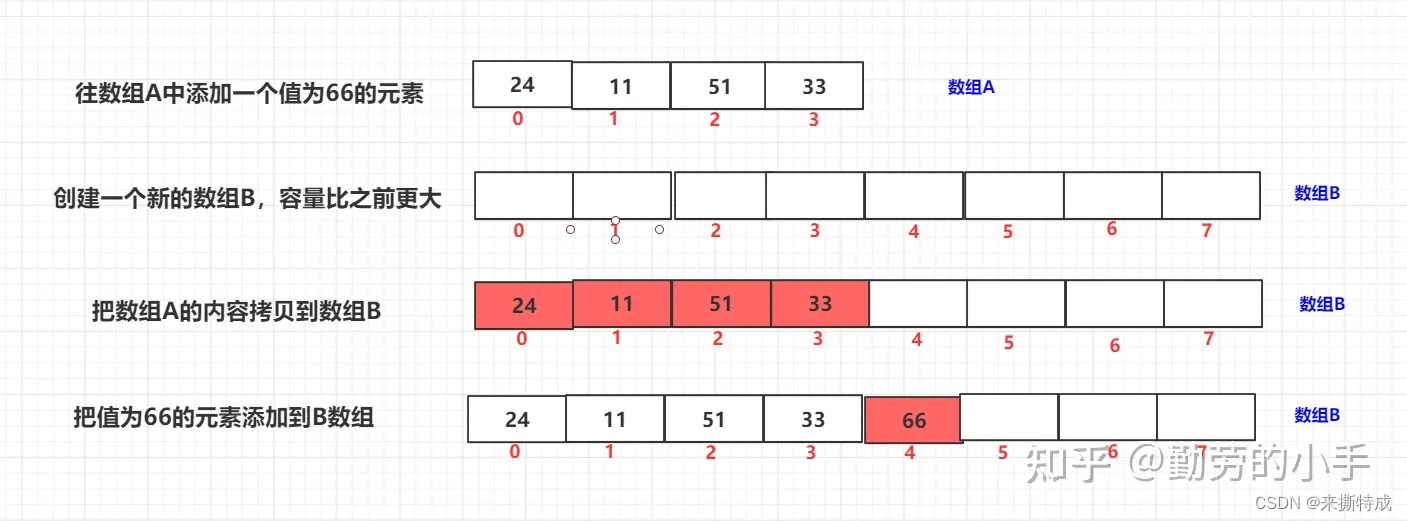
链表

有了对数组的了解，那么我们再来看链表就会有更深刻的理解了，从数组的特性上来看，数组在通过索引读取元素的时候非常快，但是在插入、删除元素的时候就比较慢了，然后数组还有一个需要扩容的过程麻烦事。 所以数组的这些劣势就势必要通过另外一种数据结构来解决了，它就是链表。

链表是一种不要求内存连续的顺序存储数据结构，它的数据节点可以分布在内存中的各个地方，节点之间是各自记录着下一个元素的指针，通过指针把所有节点串联起来组成了一条链装的结构。

在内存中链表中的节点可能分布在各个区域

?

为了美观和方便理解，我们通常会描述成这样。

链表查找元素的过程

与数组不同的是，链表查找元素的过程是比较暴力的，因为各个节点只记录了下一个节点的指针，获取元素只能从第一个节点开始逐个往后找到自己想要的元素。比如我要从链表中找到第三个元素，那么我就必须先找到第一个元素，然后通过第一元素的nex指针找到第二个元素，然后又通过第二个元素的nex指针才找到第三个元素。链表读取的元素越靠后，那么遍历链表的节点就越多，这个查找元素过程的时间复杂度为O(n)。

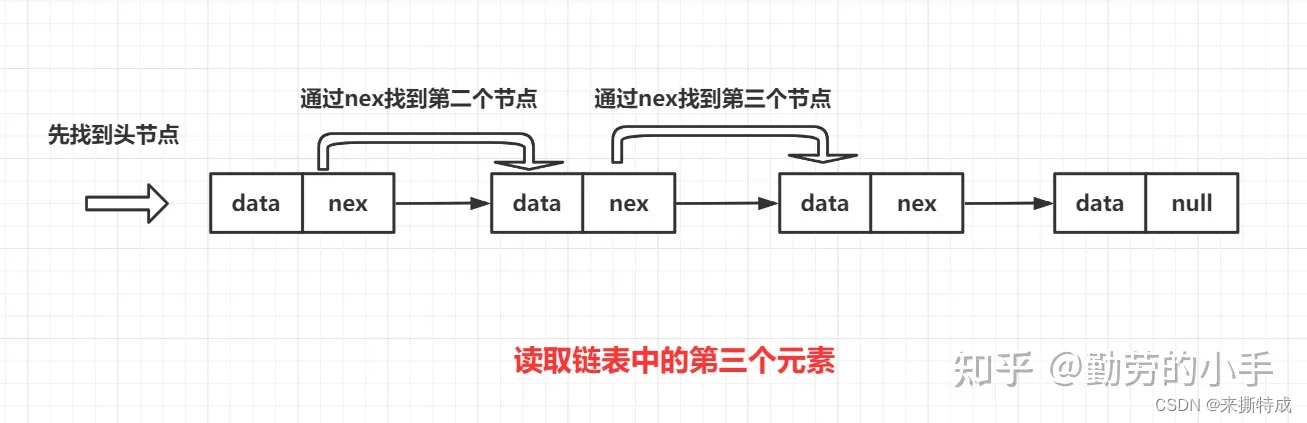
链表的插入、删除过程

因为链表并不需要保证内存空间的连续性，所以它不需要像数组一样需要挪动后面的元素，往链表中插入和删除一个元素要比数组要简单，我们只需要把插入位置前面一个节点的nex指针指向当前插入的节点，然后把当前插入的节点nex插入位置的下一个节点,。删除节点就更简单了，删除节点的时候只需要把需要删除的节点前一个元素nex指针 直接指向删除节点的下一个元素即可。

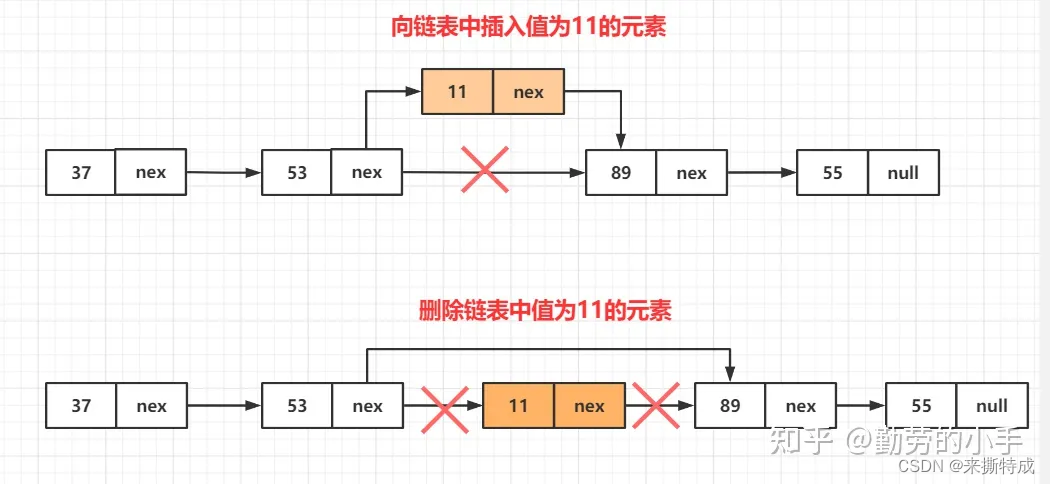
从上面的图中我们可以看出来，不管是向链表中插入新元素，还是从链表中删除元素，我们需要变更得只有前面节点的指针，不需要对任何其他元素挪动，只需要一次操作即可，整个操作过程的时间复杂度为O(1)。

?

总结

最后我们综合对比一下两个数据结构各自的特点，以便我们跟全面的了解两种数据结构的特点。

1、从性能方面对比

数组使用索引读取元素性能要比链表快

因为数组内存空间是连续的，并且每个元素所分配的空间统一，所以可以直接通过计算偏移量得到对应元素位置，不论元素在数组哪个位置，我们都可以通过一次计算得到元素的位置，整个过程的时间复杂度为O(1)。而链表则需要从第一个节点开始遍历找到对应的元素，遍历的次数受元素在链表中的位置影响，整个过程时间复杂度为O(n)。 不过需要提醒一点的是数组是在使用索引读取元素的情况下时间复杂度才是O(1)，如果不知道索引，那么也只能逐个去遍历数组的元素。

链表删除和插入元素的性能要比数组要快

数组在插入和删除节点的时候都需要挪动后面的元素，如果插入或删除的元素越靠前，那么需要挪动的元素就越多，整个过程的时间复杂度为O(n)，而链表不管删除哪个位置的元素，都只需要修改一下节点的指针即可，整个操作的时间复杂度为O(1)。

数组数据跟容易利用到CPU缓存

因为数组的空间是连续性的，而我们内存读取时候并非只回读取一个元素，而是会根据就近原则把相邻的数据一起读取出来，读取出来的数据会被CPU等缓存组件缓存起来，所以说数组的数据更容易利用到CPU的缓存。

2、从空间方面对比

链表元素占用的空间要比数组元素占用空间大

因为链表的每个元素需要额外存储一个nex指针，双向链表中还会多一个 pre的指针指向前一个节点，所以链表中的元素会比数组元素占用的空间会多一点。

数组容易造成空间浪费

因为数组的内存空间都是预先申请的，创建一个长度为10的数组就必须向内存申请能10个长度大小的内存空间，但很显然这些空间并非能马上利用到，在很长一段时间里也许一部分的数组空间都是没使用的，所以这种预先申请的内存资源势必也会造成浪费。但是链表就不会有这个问题，链表不需要预先定义长度，而是在元素真的创建完之后添加到链表里面即可。

数组的连内存续性导致无法使用碎片空间

因为数组需要的内存空间是连续的，所以在申请内存的时候只有内存存在足够的连续空间才能申请成功，然后这样有时候也会导致一个问题，就是其实内存明明有足够的空间，但是因为空间不是连续的就会导致数组无法创建。而链表的元素可以在内存的任何地方，元素之间只需要通过指针建立联系即可。

数组需要进行扩容操作

数组的长度是固定的并且无法更改，当添加超过其长度的元素时候就必须重新创建一个更大的数组来保存数据。数组扩容的过程也是实际使用中需要考虑的性能问题；而链表则不同，链表链表长度理论上是无限的，只要有足够的内存就可以无限的增加链表的长度。

?

?

?