2397. 被列覆盖的最多行数

给你一个下标从?0?开始、大小为?m x n?的二进制矩阵?matrix?；另给你一个整数?numSelect，表示你必须从?matrix?中选择的?不同?列的数量。

如果一行中所有的?1?都被你选中的列所覆盖，则认为这一行被?覆盖?了。

形式上，假设?s = {c1, c2, ...., cnumSelect}?是你选择的列的集合。对于矩阵中的某一行?row?，如果满足下述条件，则认为这一行被集合?s?覆盖：

• 对于满足?matrix[row][col] == 1?的每个单元格?matrix[row][col]（0 <= col <= n - 1），col?均存在于?s?中，或者
• row?中?不存在?值为?1?的单元格。

你需要从矩阵中选出?numSelect?个列，使集合覆盖的行数最大化。

返回一个整数，表示可以由?numSelect?列构成的集合?覆盖?的?最大行数?。

示例 1：

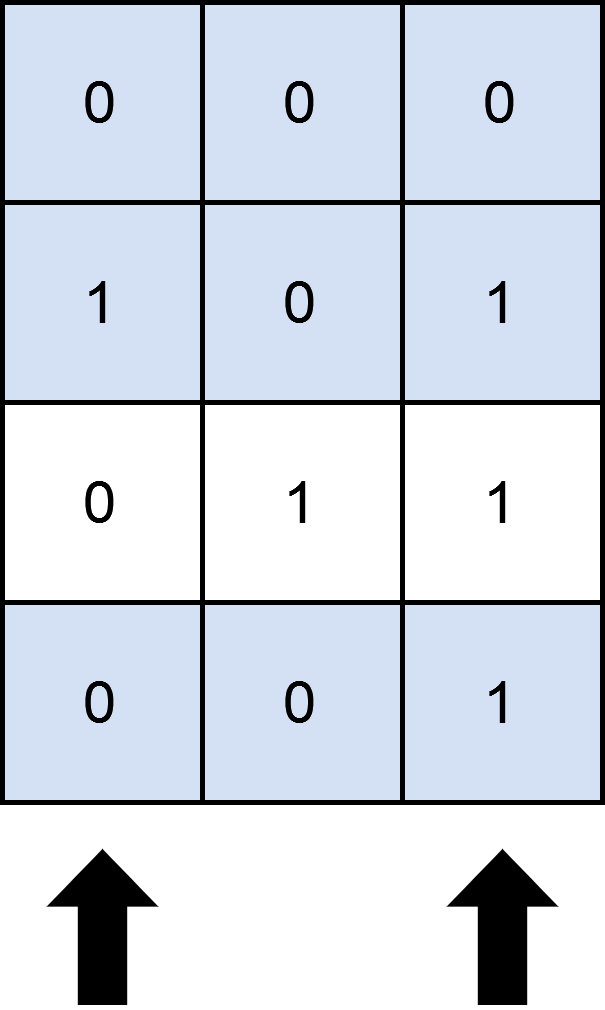
输入：matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
输出：3
解释：
图示中显示了一种覆盖 3 行的可行办法。
选择 s = {0, 2} 。
- 第 0 行被覆盖，因为其中没有出现 1 。
- 第 1 行被覆盖，因为值为 1 的两列（即 0 和 2）均存在于 s 中。
- 第 2 行未被覆盖，因为 matrix[2][1] == 1 但是 1 未存在于 s 中。
- 第 3 行被覆盖，因为 matrix[2][2] == 1 且 2 存在于 s 中。
因此，可以覆盖 3 行。
另外 s = {1, 2} 也可以覆盖 3 行，但可以证明无法覆盖更多行。

示例 2：

输入：matrix = [[1],[0]], numSelect = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，因为整个矩阵都被覆盖了。
所以我们返回 2 。

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 12
• matrix[i][j]?要么是?0?要么是?1
• 1 <= numSelect?<= n

题解：

code：

     public int maximumRows(int[][] matrix, int numSelect) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[] mask = new int[m];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 1) {
                    mask[i] += matrix[i][j] << (n - j - 1);
                }
            }
        }

        int res = 0;
        int cur = 0;
        int limit = (1 << n);
        while (++cur < limit) {
            if (Integer.bitCount(cur) != numSelect) {
                continue;
            }
            int t = 0;
            for (int j = 0; j < m; j++) {
                if ((mask[j] & cur) == mask[j]) {
                    t++;
                }
            }
            res = Math.max(res, t);
        }
        return res;
    }