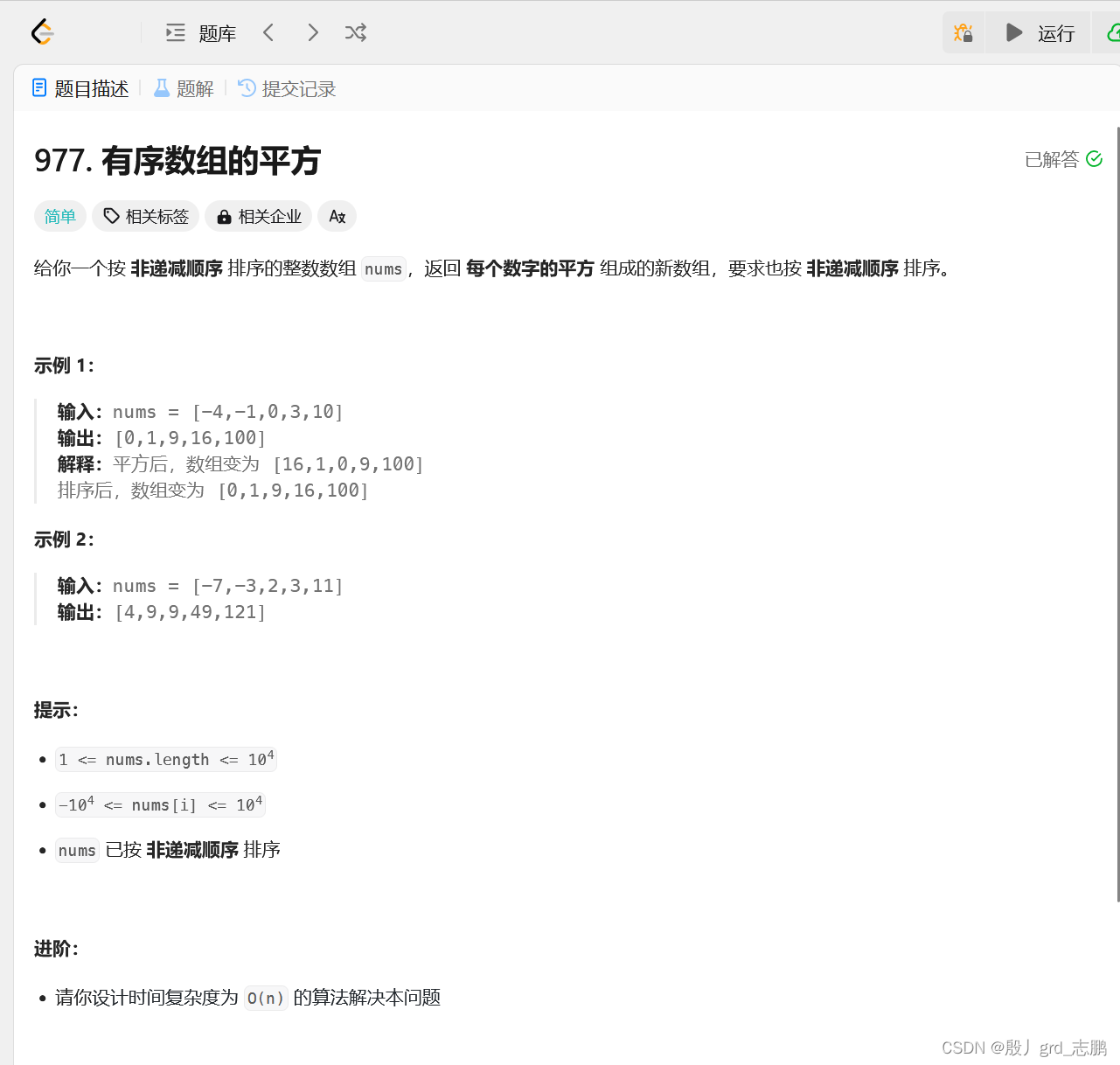
java数据结构与算法刷题-----LeetCode977. 有序数组的平方
发布时间:2024年01月18日
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
1. 时间复杂度 = 空间复杂度 = O(n * l o g 2 n log_2{n} log2?n)
| 解题思路 |
|---|
- 最直接的想法就是先算出每个元素的平方和,然后排序,所以排序的效率就是这个算法的效率。那么目前综合性能比最好,实现也简单的就是快速排序算法,它的时间和空间复杂度为O(n * l o g 2 n log_2{n} log2?n)
| 快速排序https://blog.csdn.net/grd_java/article/details/135671368 |
|---|
| 代码:时间复杂度O(n * l o g 2 n log_2{n} log2?n).空间复杂度O(n * l o g 2 n log_2{n} log2?n) |
|---|
class Solution {
public int[] sortedSquares(int[] nums) {
for (int i = 0; i < nums.length; i++) {
nums[i] = (int)Math.pow(nums[i],2.0);
}
// quickSort(nums);
Arrays.sort(nums);
return nums;
}
/**快速排序,不稳定,时间复杂度O(n * logn) 空间复杂度O(n*logn)
* 这里是快排入口
*/
public void quickSort(int arr[]){
quickSort(arr,0,arr.length-1);
}
/**
* 递归主要用于分割左右两个表
*/
public void quickSort(int arr[],int low,int high){
if(low<high){//如果左指针超过右指针,表示本次比较完成
//快速排序,每一趟都会确定一个元素的最终位置,用pivot表示,pivot是枢纽的意思
int pivotPosition = quickSortPartition(arr, low, high);
//由pivot为分界点,分成左右两个表
quickSort(arr,low,pivotPosition-1);//左表排序
quickSort(arr,pivotPosition+1,high);//右表排序
}
}
/**
* 这里是每一趟的快速排序代码,指定一个元素作为枢纽pivot,然后以它为中心,小的元素放在它左边,大的放在它右边
*/
public int quickSortPartition(int arr[],int low,int high){
int pivot = arr[low];//指定枢纽
while (low<high){
while(low<high && arr[high]>=pivot) --high;//从右边找到比枢纽小的
arr[low] = arr[high];//放在左边
while(low<high && arr[low]<=pivot) ++low;//从左找到比枢纽大的
arr[high] = arr[low];//放在右边
}
arr[low] = pivot;//最终将枢纽放到它最终的位置
return low;//最终low指向枢纽最终位置
}
}
2. 时间复杂度O(n),空间复杂度O(1)
其实直接用排序算法,有些太奢侈了,而上面快速排序主要用双指针的思想。那么我们直接用双指针做这道题,是不是更好呢?
| 代码:时间复杂度O(n).空间复杂度O(1) |
|---|
class Solution {
public int[] sortedSquares(int[] nums) {
int n = nums.length;//数组长度
int low = 0, high = n -1;//左右指针
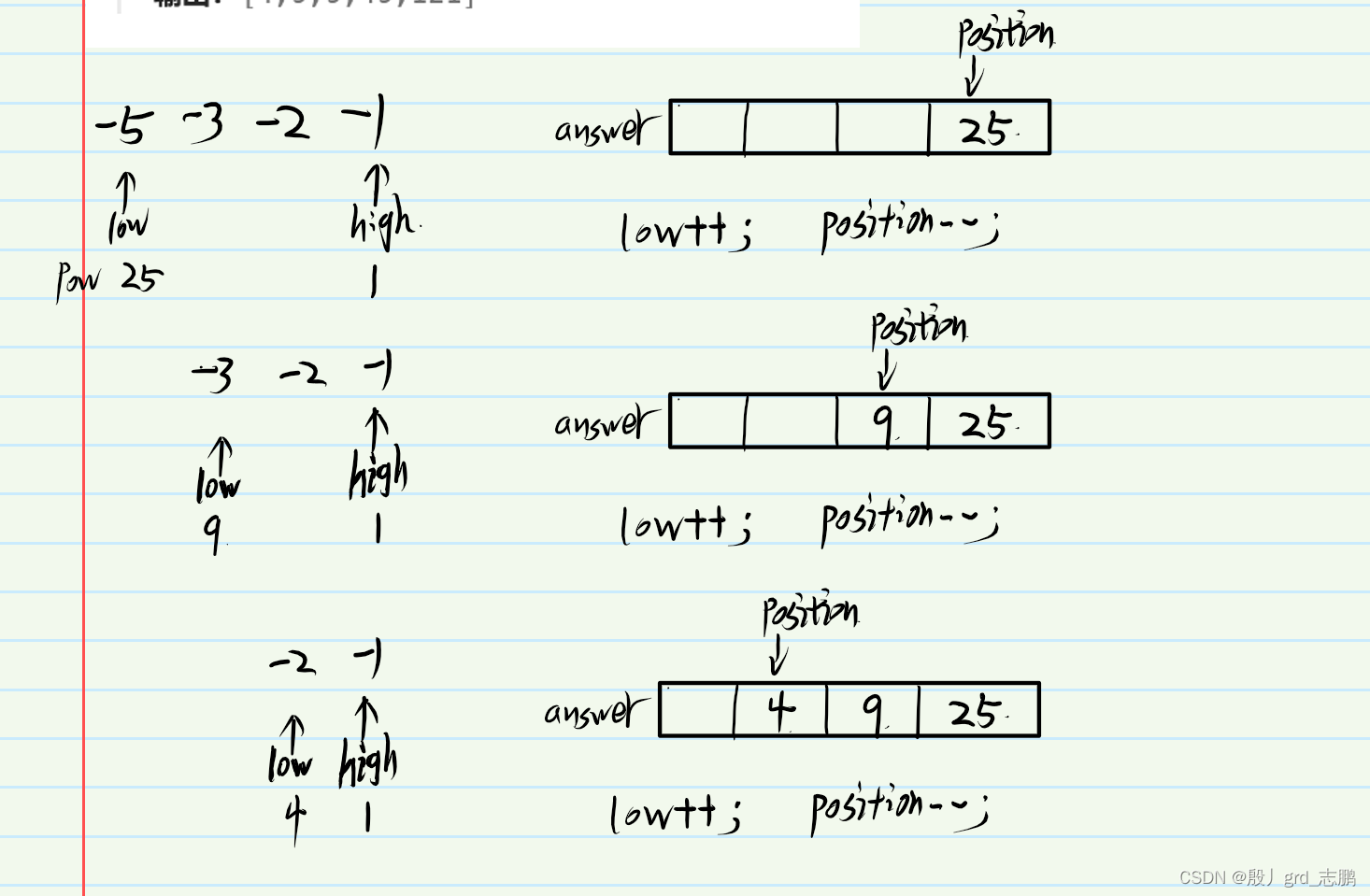
int position = n-1;//答案数组的指针,从后向前,依次指向插入元素的位置
int[] answer = new int[n];//每次都将较大值从后向前插入position指向的位置
while(high >= low){
int leftPow = nums[low]*nums[low];//获取边的平方和
int rightPow = nums[high] * nums[high];//获取右边的平方和
//将较大的插入answer数组,并移动指针
if(leftPow > rightPow) {answer[position] = leftPow; low++;}//左边的插入answer,左指针向右移
else {answer[position] = rightPow; high--;}//右边元素插入answer,右指针向左移动
position --;//指向下一个插入位置,从后往前依次插入
}
return answer;
}
}
文章来源:https://blog.csdn.net/grd_java/article/details/135668254
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- C# WPF上位机开发(WebApi联调)
- 大数据开发之Hadoop(HDFS)
- 【NR技术】 Inter-gNB-DU 条件切换或条件Pcell变更
- 介绍 Docker 的基本概念和优势,以及在应用程序开发中的实际应用。
- 文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《面向日内省间电力现货市场的区域电网交易通道可用输电能力优化方法》
- Error loading MySQLdb module.Did you install mysqlclient?报错解决方法
- 进制转换-十进制转16进制\16进制转十进制
- 腾讯云轻量应用服务器购买流程(两种方式)
- Flink Kubernetes Operator 介绍
- Linux进程管理