【从零开始学习JAVA集合 | 第一篇】深入解读HashMap源码（含面试题）
目录
目录
前言：
HashMap 是 Java 中最常用的数据结构之一，它提供了快速的查找、插入和删除操作，可以满足大多数情况下的需求。然而，要深入理解 HashMap 的内部实现和工作原理并不是一件容易的事情。本篇文章旨在深入解读 HashMap，包括其内部结构、工作原理、常见的使用场景以及性能优化等方面。
通过本文的阅读，读者将能够更好地掌握 HashMap 的工作原理，了解其在实际项目中的应用，并能够在需要时根据特定需求进行合理的选择和优化。希望本文能够成为读者学习和掌握 HashMap 的良好起点，为大家在日常编程中应用 HashMap 提供指导和帮助。
HashMap简介：
HashMap 是 Java 中的一个常用数据结构，用于存储键值对（key-value pairs）。它基于哈希表（hash table）实现，允许 null 键和 null 值，并且具有快速的查找、插入和删除操作。HashMap 继承自抽象类 AbstractMap，并且实现了 Map 接口。
这里有一个有趣的知识点：HashMap既继承了，又实现了Map接口。但是明明AbstractMap就已经实现了Map接口，为什么HashMap不直接使用父类AbstractMap的Map接口呢？
据Java集合框架创始人所说：自己在写这段逻辑代码的时候，错误的使用了这种方式，但当时以为? 不让HashMap直接继承父类的接口可能在以后会有用，而直到现在这种方式也没有表现出什么作用，而目前的JDK维护者认为其是一个无关紧要的问题，因此也就没有对这里进行修改。
HashMap 的内部结构主要由数组和链表。它通过计算键的哈希值来决定存储位置，使用链表法来解决哈希冲突。当链表的长度大于等于8并且数组的长度大于64的时候，链表就会转为红黑树
当链表的长度等于大于8，但是数组的长度小于64的时候，此时会选择对数组进行扩容而不是将链表转化为红黑树，这是因为在数据量比较小的情况下，使用红黑树反而会降低查询效率。
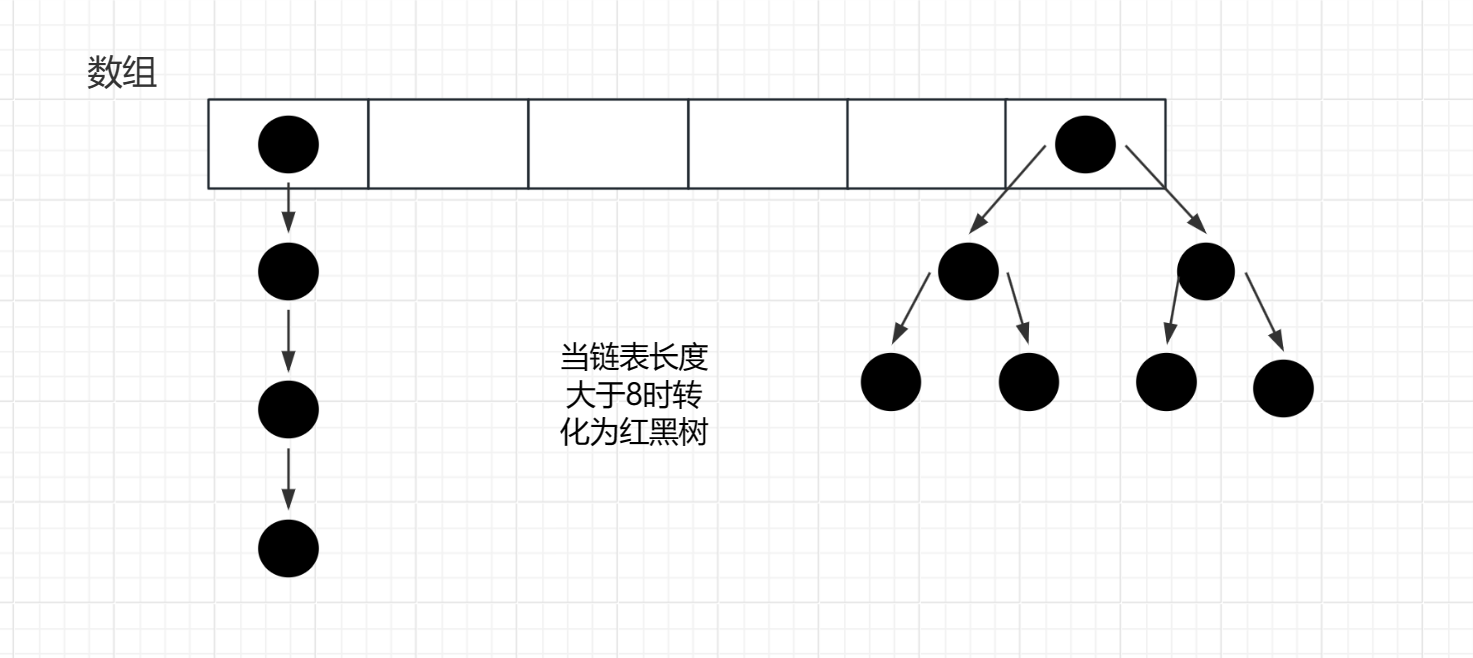
我们来总结一下HashMap的特点：
- 存取无序
- 键和值的位置都可以是null，但是键的位置只能是一个null
- 键的位置是唯一的，底层的数据结构控制键
- JDK1.8之前的数据结构是：链表+数组，JDK?1.8后是链表+数组+红黑树
- 链表长度大于8并且数组长度大于64，才会将链表转化为红黑树，变为红黑树的目的是为了高效的查询
- HashMap是线程不安全的，但由于整个类都是无锁结构，因此效率比较高
HashMap的常用常量和变量：?
1.序列化版本号常量：
private static final long serialVersionUID = 362498820763181265L;?2.集合的初始化容量（必须是2的n次幂）：
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 163.负载因子常量：
static final float DEFAULT_LOAD_FACTOR = 0.75f;4.链表转红黑树时最小链表长度常量：
static final int TREEIFY_THRESHOLD = 8;5.链表转红黑树时最小数组长度常量：
static final int MIN_TREEIFY_CAPACITY = 64;6.红黑树转为链表的最小数组长度常量
static final int UNTREEIFY_THRESHOLD = 6;
6.数组阈值（调整下一次扩容的容量值）（容量 * 负载因子）
int threshold;7.负载因子变量：
final float loadFactor;8.存储元素的数组：
transient Node<K,V>[] table;?9.存放具体元素的集合：
transient Set<Map.Entry<K,V>> entrySet;10.实际存储元素的个数：
transient int size;11. 记录HashMap的修改次数：
transient int modCount;HashMap的重要考点：?
HashMap的存储过程：
在JDK1.8之前，HashMap由数组+链表 数据结构组成。
在JDK1.8以后，HashMap由数组+链表+红黑树 数据结构组成。
而本文我们只讲讲解基于数组+链表+红黑树的HashMap。我们接下来用一个实例来讲解HashMap的存储过程。
public class Demo01 {
public static void main(String[] args) {
HashMap hashMap = new HashMap<String, Integer>();
hashMap.put("a", 1);
hashMap.put("b", 2);
hashMap.put("c", 3);
System.out.println(hashMap);
}
}当我们执行存储操作的时候，会发生如下操作：
- 计算哈希值：当调用put方法时，HashMap会将传入的key通过哈希函数（hash function）转换为一个整数，这个整数被称为哈希值。
- 计算数组索引：HashMap使用哈希值对数组的长度进行取模运算，得到一个数组索引（即数组的位置），用于确定键值对在数组中的存储位置。
- 存储链表或红黑树：如果该位置上已经有其他键值对存在，那么新的键值对将会以链表或红黑树的形式插入到该位置的末尾或中间。如果该位置还没有任何键值对，那么直接将键值对存储到该位置。
需要注意的是：在JDK8之前，HashMap的构造方法就会帮我们创建一个长度为16的Entry[] table 用来存储键值数据。在JDK8以后就不是在HashMap的构造方法底层来创建数组了，而是在第一次调用put方法的时候创建一个Node[] table 来存储键值对数据。
好的，我们现在已经基本了解了HashMap是怎么插入一个数据的，接下来让我们看一下put方法的源码：
我们转到putVal中查看一下：
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
小插入：?
我们对Key调用了哈希算法得到了一个int类型的整数，而这个哈希算法的底层逻辑是采用Key的HashCode方法的值结合数组长度进行无符号右移（>>）,按位异或（^）
这个计算方式相对于直接使用hashCode()方法的好处在于，可以减少哈希冲突的概率。通过将二进制位的高位和低位都参与到哈希值的计算中，可以更好地保持哈希值的随机性和分布性，从而减少不同键的哈希冲突，提高HashMap的性能。
其实我们还有不少的方法同样可以得到一个hash值，比如取余。但位运算是硬件操作，可以直接在CPU的寄存器中进行操作，效率要高得多。因此我们一般都会使用位运算代替取余。而用位运算代替算术运算在后面还很常见，我们在这里要有这样的认识。
并且通过这个方法我们也可以看出：HashMap的Key是可以为null的。当Key为null的时候，将位置0作为键值对的插入位置。?
现在让我们现在正式的开始解析这段代码：
- 首先，代码将table赋值给变量tab，并进行判空操作。如果table为空，则说明哈希表尚未初始化，此时将n设为0。
- 如果table不为空，则将table的长度赋值给变量n。
- 接下来，通过条件运算符判断n是否为0，如果是0，则表明哈希表的长度为0，需要进行扩容操作。在这种情况下，代码会调用resize()方法进行哈希表的扩容，并将扩容后的哈希表赋值给tab，并将扩容后的哈希表的长度赋值给n。
- 最后，返回n作为哈希表的长度。
总的来说，这段代码的作用是获取哈希表的长度，并在需要扩容时进行相应的处理。通过检查哈希表的长度是否为0，可以判断哈希表是否需要进行初始化或者扩容，从而保证HashMap的正常使用和性能优化。
- 首先，代码计算出要插入的位置i，通过对hash值进行(n-1) & hash的位与运算得到。这里的n是哈希表的长度，通常是2的幂，通过这个位与运算可以将hash值限定在0到n-1之间，确保落在哈希表范围内。
- 然后，代码判断tab[i]位置是否为空，即当前位置是否已经存在节点。如果为空，则将新节点插入到这个位置。
- 如果tab[i]位置不为空，则说明当前位置已经存在节点。这里可能会涉及到链表或者红黑树等数据结构，用于处理哈希冲突的情况，但在这段代码中没有展现出来。
总的来说，这段代码的作用是根据hash值找到对应的位置，然后判断该位置是否已经存在节点，如果不存在则直接插入新节点，如果存在则根据具体的情况进行相应的处理，以保证HashMap中的键值对能够正确存储和检索。
- 首先，代码定义了一个Node和一个K类型的变量k。然后通过一系列的条件判断来确定如何处理哈希冲突:
- 首先，判断当前节点p的哈希值和键与要插入的哈希值和键是否相等，如果相等，则将当前节点p赋值给e。
- 如果不相等，且当前节点p是TreeNode类型，则调用TreeNode的putTreeVal方法来处理插入。
- 如果以上两个条件都不满足，则通过遍历链表的方式找到合适的位置插入新节点，同时处理可能出现的树化操作。
总的来说，这段代码的作用是处理哈希冲突的情况，具体处理方式取决于当前节点的类型以及与要插入节点的哈希值和键的比较结果。通过合适的处理方式，保证HashMap在处理哈希冲突时能够正确地插入新节点，并维护数据结构的完整性。
-
首先，将已存在节点e的值赋给oldValue，以便在后面返回旧的值。
-
然后会根据onlyIfAbsent的取值来判断是否需要覆盖已存在节点e的值：
- 如果onlyIfAbsent为false，或者oldValue为null（即允许替换已有的空值），则将新值value赋给节点e的值e.value。
-
接着调用afterNodeAccess(e)方法来进行相关操作，比如LinkedHashMap中重写的方法会将节点移动到链表末尾，以实现LRU策略。
-
最后返回旧的值oldValue，表示已存在键对应的旧值。
总的来说，这段代码的作用是在HashMap中处理键已存在的情况，根据需要更新节点的值，并在操作后返回旧的值。
-
首先，对modCount进行自增操作，用于在并发情况下对HashMap的修改进行控制。
-
然后对size进行自增操作，表示当前HashMap中键值对的数量增加了1。接着会检查size是否超过了阈值threshold，如果超过了则需要进行哈希表的扩容操作。
-
如果size超过了threshold，就调用resize方法对哈希表进行扩容。哈希表的扩容会重新计算每个键值对的位置，以降低哈希冲突的概率。
-
接着调用afterNodeInsertion(evict)方法来进行相关操作，其中evict参数表示是否需要进行LRU策略的节点移除操作。
-
最后返回null，表示插入操作完成并且不需要返回任何值。
总的来说，这段代码的作用是在HashMap中处理插入新节点后更新相关计数器、进行哈希表的扩容操作，并在操作后进行相关处理。
?所以其实整个put操作的代码逻辑链其实是比较清晰的，我们可以用图表示为：
HashMap的扩容过程：
之所以要讲HashMap的扩容过程，是因为他的扩容和我们想的有点不一样，我们先看代码：
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
按照我们的传统思路来讲：当原数组进行扩容之后，当我们想要把原数组中的数据放到新数组中的时候，基本的思路是对原数据进行重新Hash计算位置，放入数组。但这样的效率太低了。HashMap的扩容并没有采用这种机制。
我们先来看源代码中HashMap的扩容是如何做的：
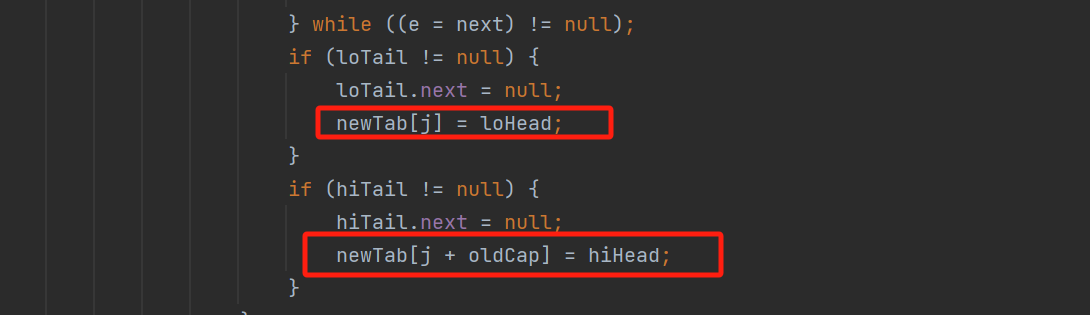
简而言之：HashMap认为：旧节点的新位置要么在原位置（newTab[j] = loHead），要么在原位置+旧容量（newTab[j + oldCap] = hiHead）上?
?我们来看一下为什么可以这么认为：
当我们进行扩容的时候，每次的大小都是翻倍的（2的n次幂），例如从4到8，16到32。这种内存翻倍后与原来计算（n-1）& hash 的结果相比，只是多了一个bit位。
例如：当我们从4 扩容的 8 的时候：
???n:
4：0100? ? ? ? 16：010000
--------------------------------------------------------------------------------------------------------------------------
8：1000? ? ? ? 32：100000
n-1 ：
3：0011? ? ? ? 15：001111
--------------------------------------------------------------------------------------------------------------------------
8：0111? ? ? ? 32：011111
也就是说实际上扩容后，从二进制来看，运算结果只有最高位发生了变化，如果元素的二进制最高位为0，那么就是原位置，如果二进制最高是1，那么就会变为1，也就是原位置+旧容量
正是因为这种巧妙的rehash的方式，大大提高了运行效率。
HashMap的初始化：
我们不讲HashMap的自动初始化，源码比较简单，大家可以自己看一看。而在这里要着重讲一下HashMap的手动扩容过程：
我们都知道：HashMap的扩容过程是一个比较浪费时间的过程。因此我们如果想要提高代码运行的效率，就要手动设置初始大小，避免自动扩容。但有的人会在这里陷入一个误区，我们通过一个实际问题来引出：
当我们要存放七个元素的时候，我们应该手动初始化大小为多少呢？
?很多同学肯定下意识的回答 8 。 但其实是错误的！让我们来思考一下：
如果设置为8 的话， 负载系数默认是0.75。那么 8 * 0.75 =6，也就是说数组中实际元素达到6个就要扩容，我们如果存放七个元素，手动设置大小为8 的话，还是避免不了扩容。?
因此：我们应该 手动设置为（需要存储的元素个数/负载因子）+1。这是计算手动设置容量的通用方法。
注意：不可以修改负载系数，0.75是官方大量数据统计出来的一个比较均衡的负载因子，我们基本不会对其做修改！
常见面试题：
1.为什么集合的初始化容量必须是2的n次幂？
首先，当我们尝试向HashMap中添加一个元素的时候，需要根据Key的hash值得到数组中的具体位置。而我们不可以直接使用Key的hash值。这是因为Key的hash值不一定就在数组下标范围内，因此我们要对Key的hash值再次进行操作，使其满足值的范围在数组下标范围内。
这里的第一个思路就是取余。我们让hash%n(数组长度)，这样就可以控制得到的值始终在数组下标范围内。
但是这里又有一个问题：如果是取余的话，效率是很低的，不如使用位运算。而我们的代码在实际中也是用位运算来代替取余操作。
而我们在实际中也是这么做的，但是hash % n 和 （n - 1）& hash 的值相等的前提是 n 是2 的 x?次幂
?而除此之外，返回到使用这个方法的最外层，我们的目的还是为了让数据能够均匀分布，减少Hash冲突。
如果创建HashMap的时候，输入的数组长度不是2的幂，那么HashMap就会通过位运算得到一个比我们输入的数组长度大的，离我们输入数组长度最近的一个2的幂。
2.hash方法为什么要右移16位异或？（(h = key.hashCode()) ^ (h >>> 16)）
其中 h = key.hashCode() ^ (h >>> 16) 的目的是为了增加哈希值的随机性，使得节点在哈希表中分布更均匀，减少哈希冲突，提高查找效率。
具体来说：
- 首先，通过?
key.hashCode()?获取键的哈希码。 - 接着，通过?
h >>> 16?将?h?右移16位，然后将结果与?h?进行异或操作?^。这样做是为了让高位的信息参与到低位的计算中，增加低位的随机性。
通过这样的运算，可以让原始的哈希值的高位和低位进行混合，并且引入了一定程度的随机性，使得最终的哈希值分布更加均匀，减少了哈希冲突的概率。这种处理方式有助于提高HashMap的性能，特别是在处理大量数据时，能够更有效地分散数据，减少链表长度，提高查找效率。
如果当哈希值的高位变化很大，低位变化很小，这样就很容易造成哈希冲突了，所以这里把高低位都利用起来，从而解决了这个问题。
3.负载因子的作用是什么
负载因子用来判断当前数组的负载程度，简单来讲就是有多少元素。当数组中的实际存在元素个数大于 数组长度 * 负载因子的 时候，就会进行扩容操作。?这点我们可以在put代码中看到：
我们可以看到当数组size大于threshold的时候，就进行扩容操作。我们可以在resize方法中看到thresould的计算方法：
?4.HashMap如何保证初始化数组长度始终是2的n次方的
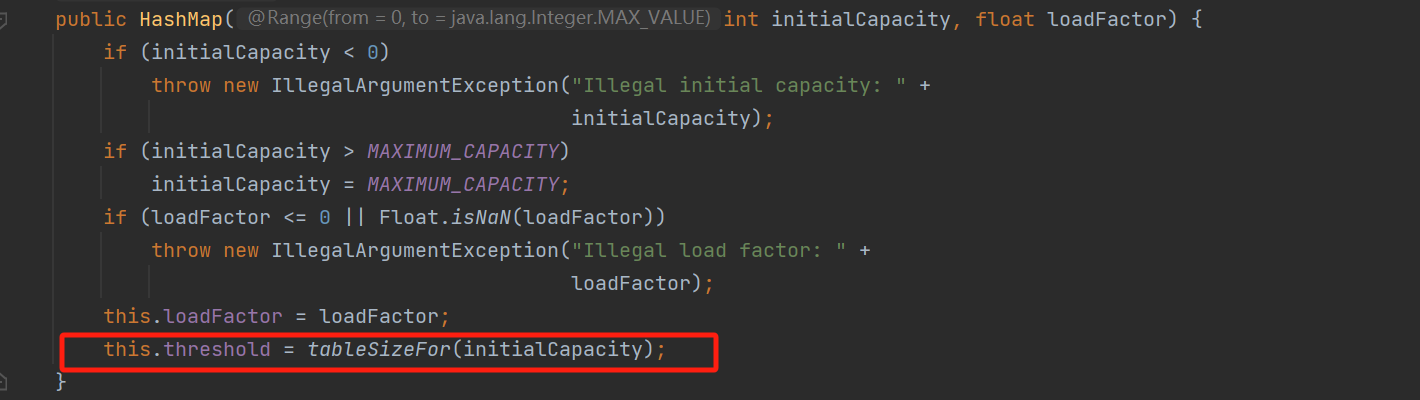?我们可以看到默认的带参构造函数对我们输入的数据进行了这样的操作，具体方法如下：
static final int tableSizeFor(int cap) {
int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}而这个方法中又调用了?Integer.numberOfLeadingZeros 方法，我们来看看：
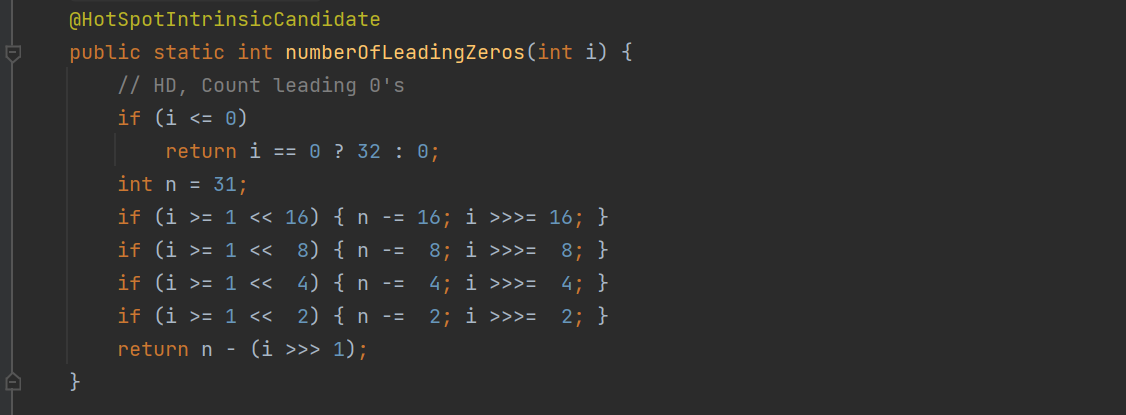
?numberOfLeadingZeros方法用来计算32位长度的二进制数字的前导零：
例如 9 的二进制：
00000000 00000000 00000000 00001001那么9的前导零就是28，我们来看看代码执行结果：
好的，让我们回到? tableSizeFor? ?方法中 ：
static final int tableSizeFor(int cap) {
int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}我们来模拟一下tableSizeFor操作：
- 输入一个数字?5。
- numberOfLeadingZeros方法 对（5-1）得到结果为：29。
- n等于-1>>>29,结果为7。
- 进入判断: n>0 则执行(n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1。
- n< MAXIMUM_CAPACITY(1<<30),则返回n+1，也就是7+1 =7
这样，我们就得到了一个比5大的，距离5最小的一个二次幂。这就是tablesizeFor的运行原理。
需要注意的是这里返回的结果并没有直接赋值给HashMap的初始实例数组长度，而是给了扩容阈值?threshould ！！！‘
而真正的初始化实际上发生在第一次调用put方法插入元素的时候：
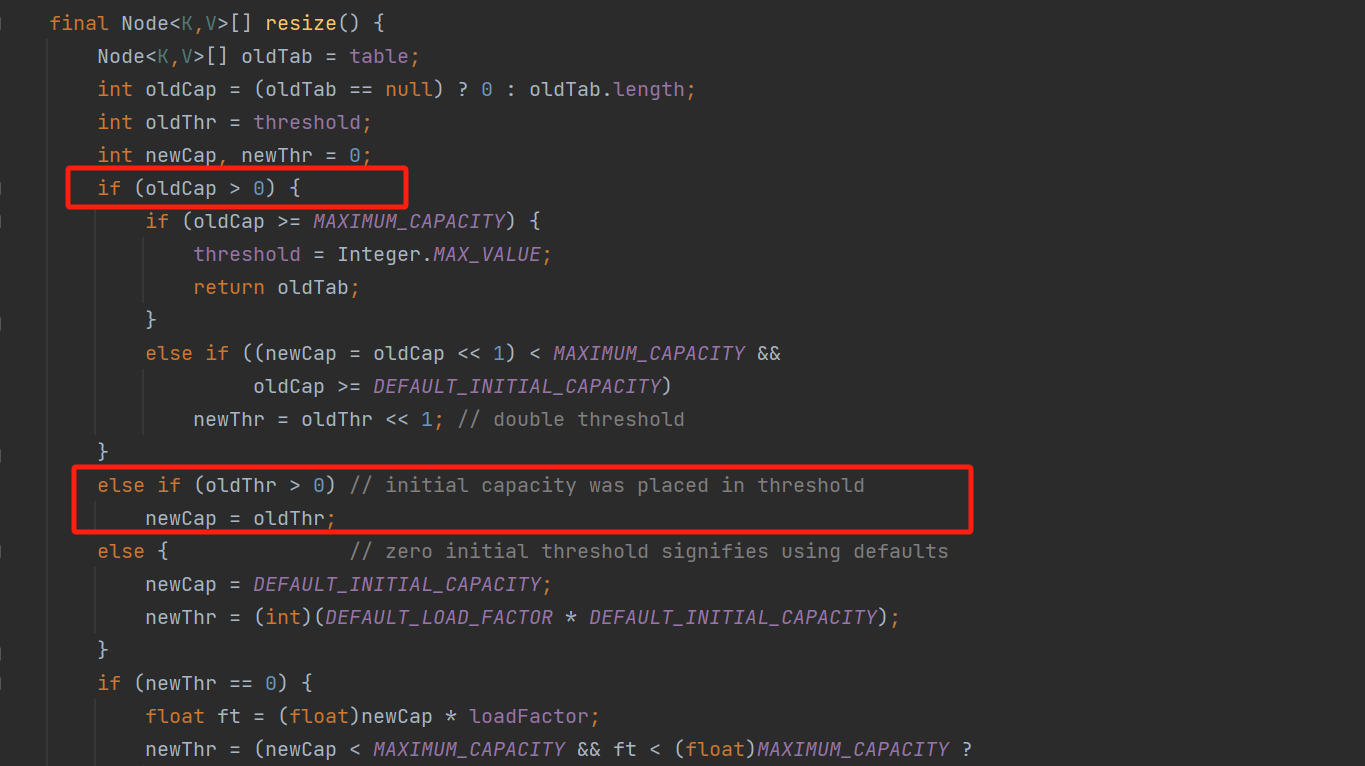
总体的逻辑为：当旧数组为空，旧阈值不为空的时候，把旧阈值赋值给新数组。?
就这样，我们就实现了带参数的HashMap实例创建。
5.HashMap将链表转化为红黑树的链表边界长度为什么是8
这个问题其实在HashMap的源码中就给了解释：
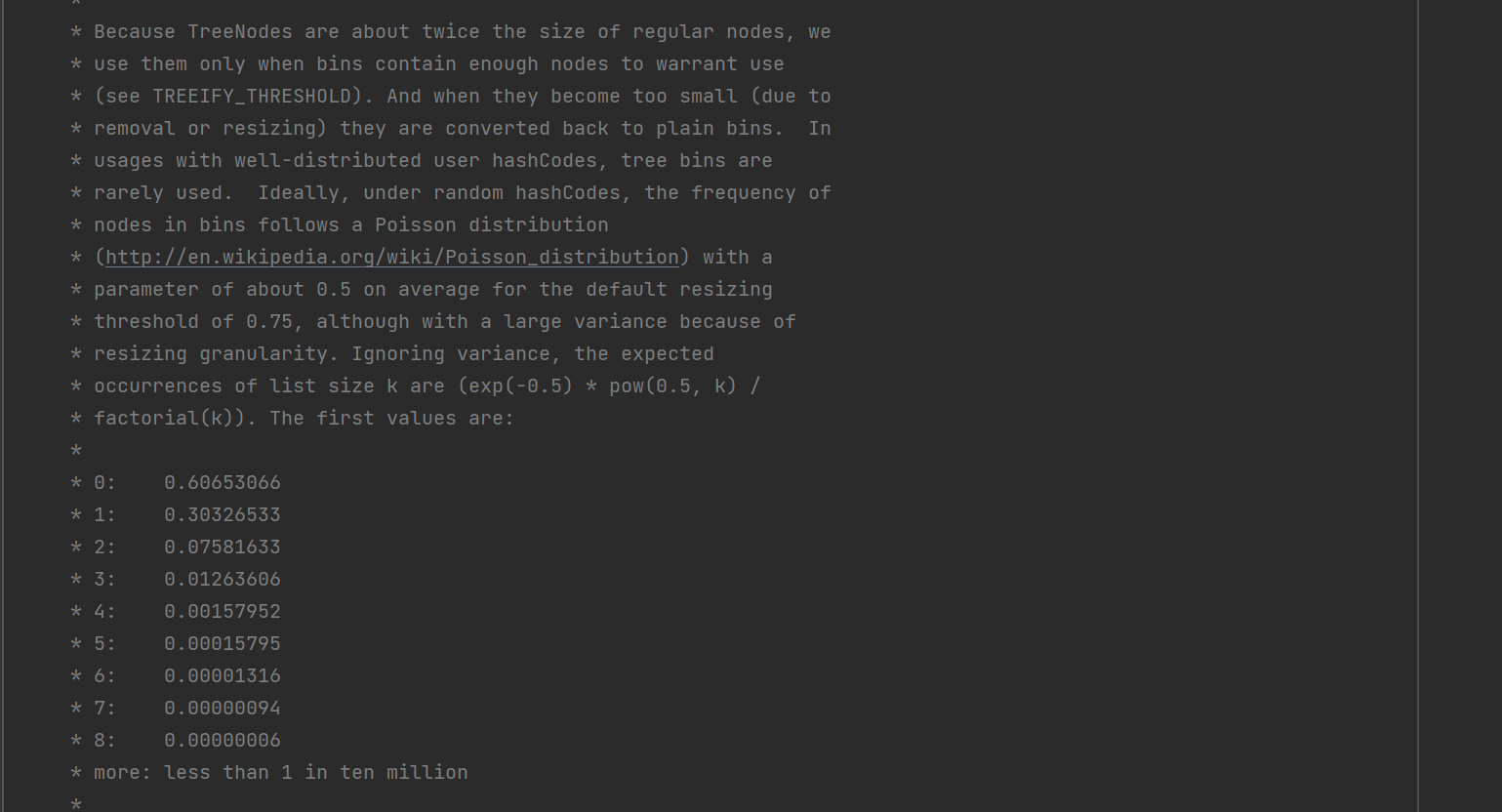
简要的意思就是：由于树节点的大小是链表节点的两倍，因此我们轻易不会将链表转化为红黑树，这会对内存造成浪费。而在大量的实际数据插入的情况下，我们统计发现：箱子中的节点的频率服从泊松分布。
当连续插到链表的第八个节点的时候，实际上概率已经很小了，已经达到了0.00000006。也就是说我们将链表的长度设置为8，就已经可以应对大多数的HashMap的Hash碰撞了?。当节点大于8的时候，我们再考虑查询的效率问题，将其转化为红黑树。
总结来讲，将链表转换红黑树的链表长度边界设置为8，是综合时间和空间的结果。
总结：
综上所述，本文深入介绍了HashMap的底层源码实现原理。首先，我们深入探讨了HashMap的数据结构，它基于数组和链表（或红黑树）实现，这使得HashMap能够高效地存储键值对。其次，我们详细分析了HashMap的哈希算法，通过hashCode方法和位运算来确定元素在数组中的位置，实现了快速的查找、插入和删除操作。对于扩容与负载因子的讨论使我们更好地理解了HashMap是如何动态调整大小以保持性能的。
通过本文的介绍，读者不仅可以深入了解HashMap的具体实现细节，还能够从中学习到在实际开发中如何更好地利用HashMap的特性。深入理解HashMap的底层源码将有助于提升对Java集合框架的整体理解，并能够在日常开发中更加灵活、高效地应用HashMap这一重要的数据结构。
如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Ansible-剧本与变量
- 鸿鹄电子招投标系统：基于Spring Boot、Mybatis、Redis和Layui的企业电子招采平台源码与立项流程
- 认识机器学习【woodwhales.cn】
- linux 常见命令
- 从0开始学C++ 第六课：控制流程和循环结构
- logback日志记录器
- Shell编程基础 – C语言风格的Bash for循环
- 【Spring 篇】基于注解的Spring事务控制详解
- C语言计算三阶行列式
- 2024年业务流程管理(BPM)的10大发展趋势