通信入门系列——离散卷积、连续卷积、卷积性质
本节目录
一、线性系统的激励响应
1、离散δ信号
2、离散卷积
3、连续δ信号
4、连续卷积
二、卷积性质
1、交换律
2、分配律
3、结合律
4、与冲激函数卷积
本节内容
一、线性系统的激励响应
输入信号又称为激励,输出信号又称为响应。一个信号输入给一个线性系统的时候,输出信号会因输入信号不同而不同。
1、离散δ信号
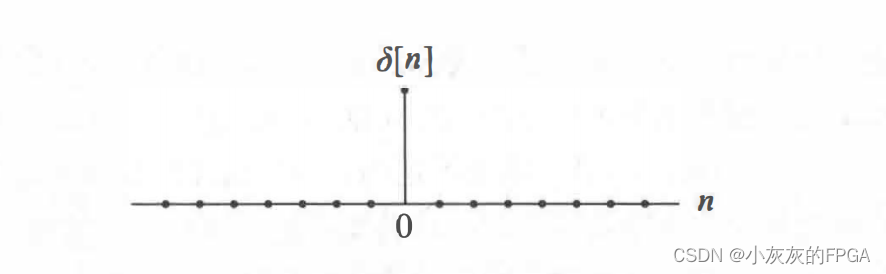
离散δ信号,又称为离散冲激序列,公式可以表述为:

离散冲激序列的图形可以表示为:
2、离散卷积
任何一个离散信号x[n]都可以表示称为如下的形式:
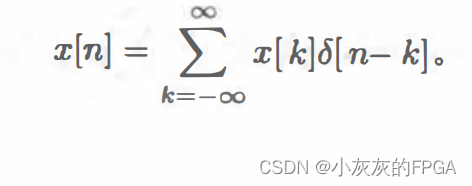
在上式中,只有当k=n时,δ[n-k]=1,其余时刻均为零,求和之后为x[n]。
假设一个离散系统H{.}是一个线性系统,根据叠加性和数乘性可知:
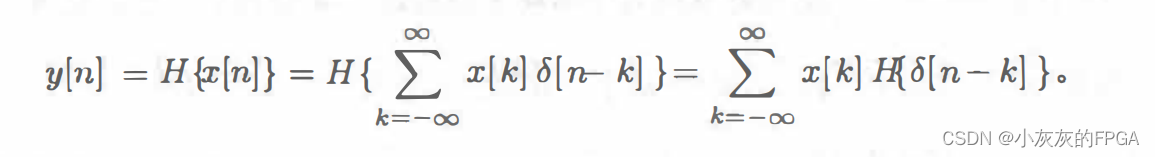
进一步可以得到:h[n-k]=H{δ[n-k]},从而带入上式中可得:
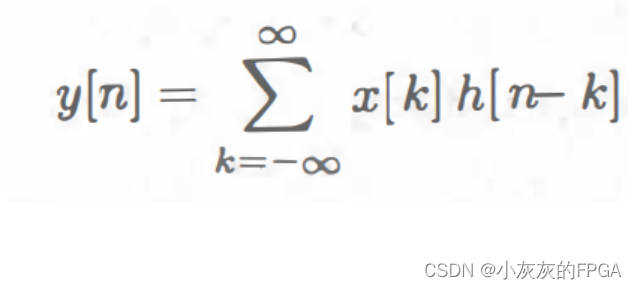
上式也就是所谓的离散卷积,y[n]=x[n]*h[n]。其中h[n]指的是系统的冲激响应,反映了系统的特性,也就是说系统的输出是输入和冲激响应的卷积。
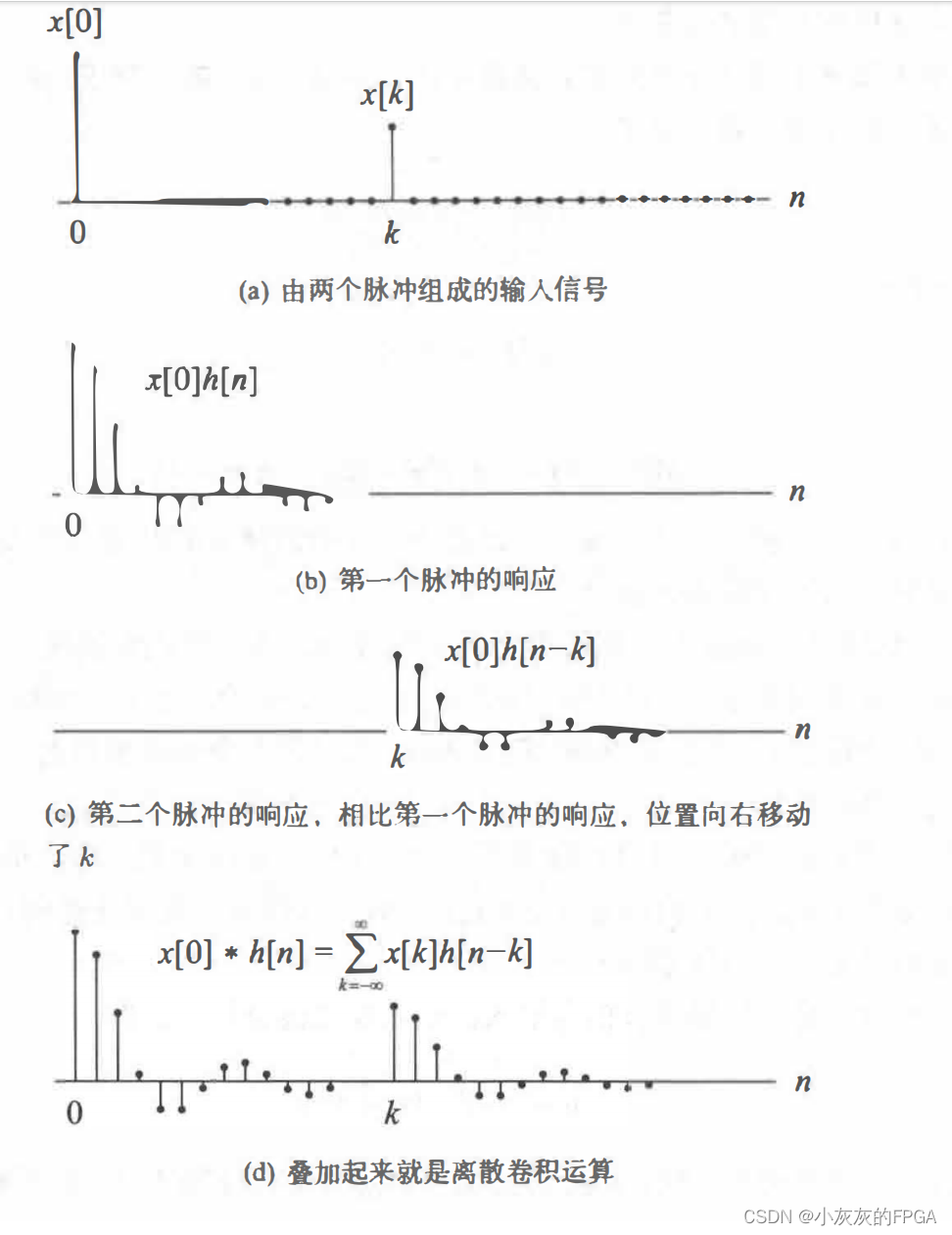
如何理解离散卷积的计算过程?
输入信号为两个脉冲,第一个脉冲位于位置0处,产生一个响应x[0]h[n],第二个脉冲位置在k处,产生一个响应x[k]h[n-k],系统的输出,也就是所谓的卷积运算,是把两个响应求和。
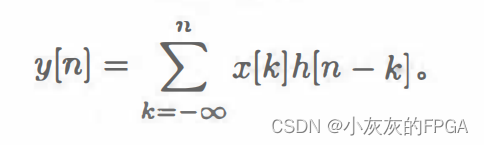
n时刻系统的输出信号只与该时刻之前的输入信号有关,和该时刻之后的输入信号无关,因此求和的上限可以取n。
3、连续δ信号
连续δ信号,也称为“狄拉克函数”或者“冲激函数”。冲激函数零点的值是无穷,其他位置的值都是零,也就是说在无穷时间上的积分为单位1,具体的公式如下:

4、连续卷积
假设一个系统y(t)=H{x(t)},其中x(t)为输入信号,y(t)为输出信号,h(t)为系统对δ信号的响应,即:h(t)=H{δ(t)}。
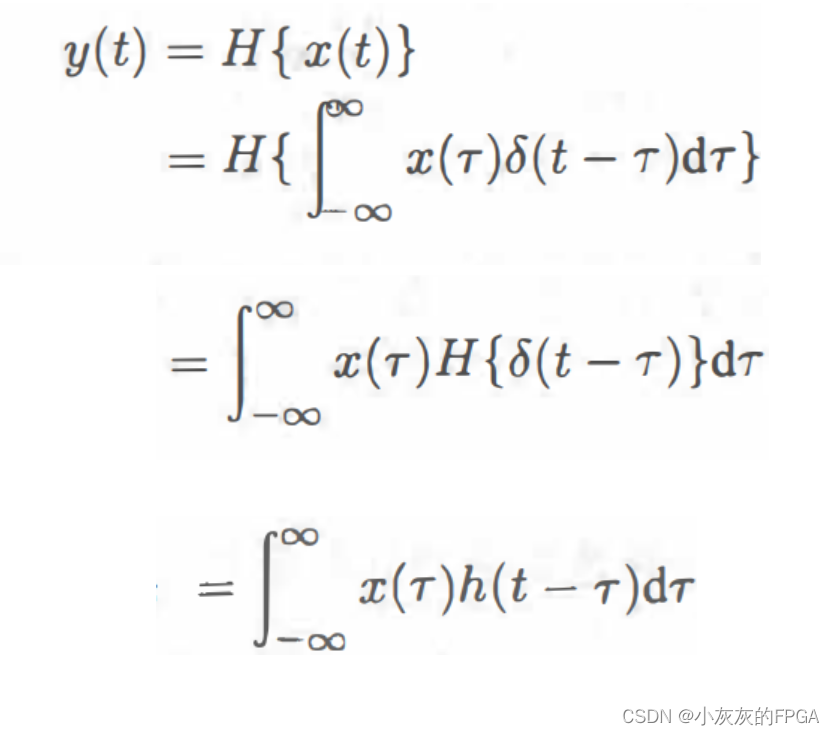
如何理解连续卷积?
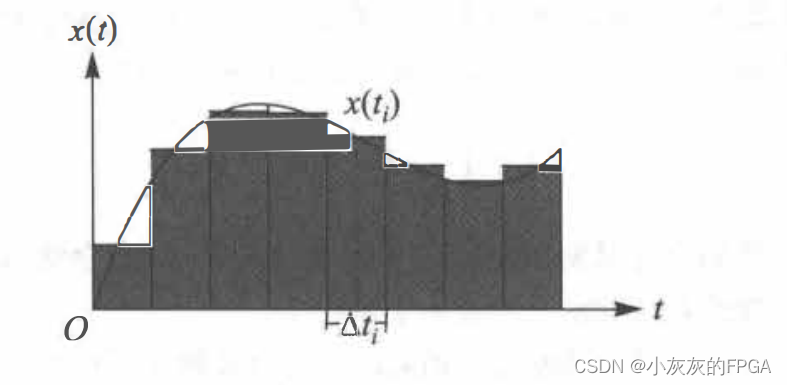
一个连续信号,通过多段的阶梯信号来逼近,将横坐标t划分成很多的小段,保证每一段内的信号水平值差不多,选择一个数值作为此段的代表,从而形成一个阶梯信号。如果每个小段的长度都趋近于零,那么阶梯信号就无限逼近于输入信号x(t)。
将等效的阶梯信号作为系统输入时,每个小的阶梯信号都会产生一个对应的输出信号。当然,等效后的阶梯信号是所有小阶梯信号的和,那么所有小阶梯信号的输出信号的和就是这个等效阶梯信号的输出响应。
如何推导并证明连续卷积?
将连续信号分解成N个阶梯,第i个阶梯的信号数值为x(ti),对应的阶梯宽度为?ti,则这个矩形脉冲的面积为x(ti)×?ti。用hi(t)表示宽度为?ti,面积为1的矩形脉冲的输出,则根据线性系统的数乘性,可知面积为x(ti)×?ti的脉冲信号的输出x(ti)×?ti×hi(t)。当单位面积的矩形脉冲的宽度趋近于零时,此时矩形脉冲为冲激信号δ(t),系统对它的响应hi(t)逼近于冲激响应h(t),也就得到x(ti)×?ti×h(t)。根据线性系统的时不变特性,将系统的响应h(t)右移ti,则可得到x(ti)×?ti×h(t-ti)。将所有的小脉冲的响应累加就是系统对x(t)的响应,公式为:
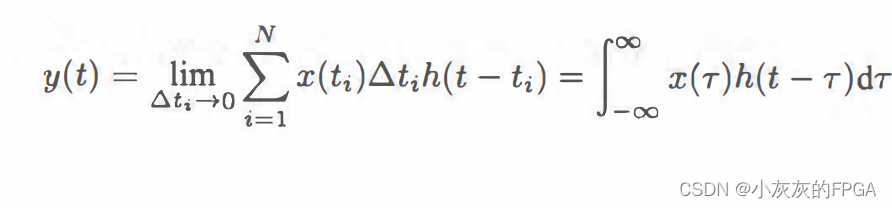
t时刻系统的输出信号只与该时刻前的输入信号有关,积分的上限取t,则y(t)可以表示为:
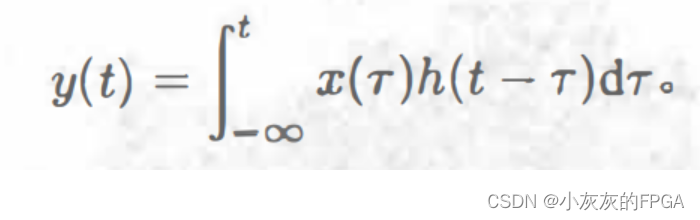
y(t)是t时刻系统的输出信号,是由t时刻之前的输入信号的无数的小冲激脉冲引起的,积分上限为t,积分变量为τ,时刻τ处的一个冲激脉冲,强度为x(τ)dτ,所引起的系统输出为x(τ)dτ×h(t-τ),也就是将冲激响应的波形右移τ,然后通过积分后得到y(t)。
二、卷积性质
1、交换律
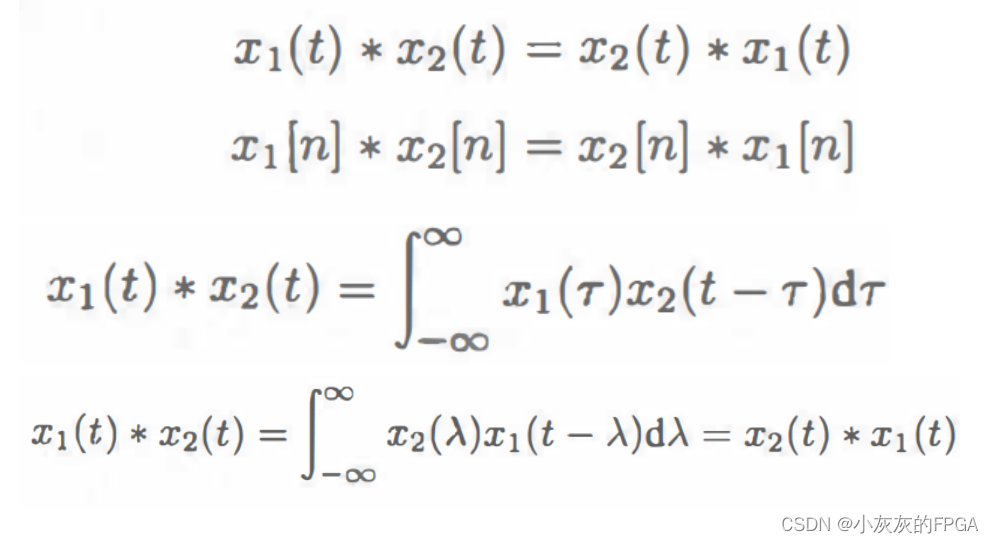
2、分配律
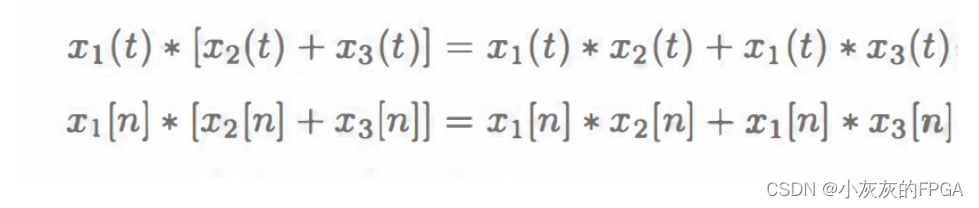
3、结合律
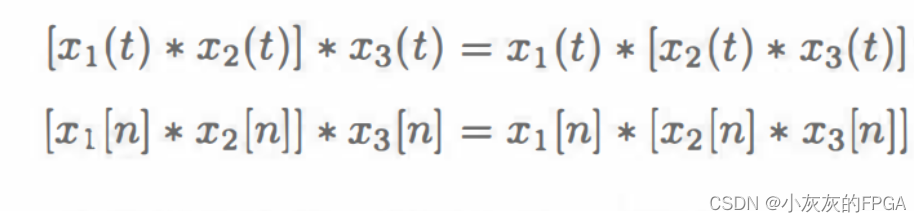
4、与冲激函数卷积
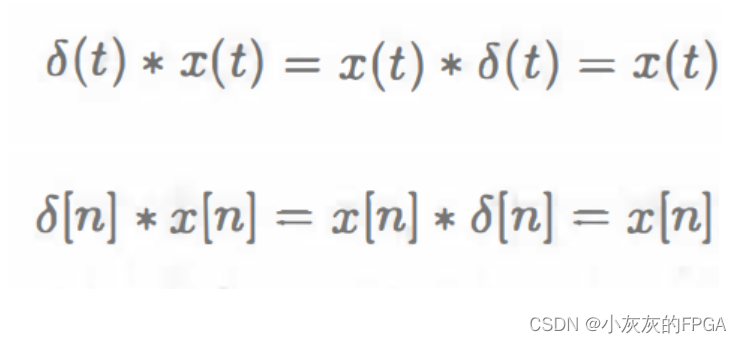
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!