顶级SCI优化！CGO-CNN-BiGRU-Attention混沌博弈优化卷积、双向GRU融合注意力机制的多变量回归预测程序！

适用平台：Matlab 2023版及以上

CGO混沌博弈优化算法，发表在SCI、中科院2区Top顶级期刊《Artifcial Intelligence Review》上。

该算法提出时间很短，目前还没有套用这个算法的高水平文献。

同样的，我们利用该物理意义明确的创新算法对我们的CNN-BiGRU-Attention时序和空间特征结合-融合注意力机制的回归预测程序代码中的超参数进行优化，构成CGO-CNN-BiGRU-Attention多变量回归预测模型.

文献解读：该文提出了一种新的元启发式算法，称为混沌博弈优化（CGO），用于求解优化问题。CGO算法的主要概念是基于混沌理论的一些原理，其中混沌博弈概念针对的是分形的配置和分形自相似性问题是。通过使用各种基准问题对CGO算法的性能进行评估，并与其他随机优化算法进行比较。结果表明，CGO在收敛性和统计数据方面优于其他优化器。

原理：在数学中，分形是欧几里得空间的一个子集，其中特定的几何图案在多个尺度上重复。分形在不同的尺度上具有大致相似的形状，将它们表示为自相似系统。著名的分形之一是曼德布洛特集，它代表了一个精心设计的不定式边界，其中多个递归细节在不同的尺度上逐渐表现出来。

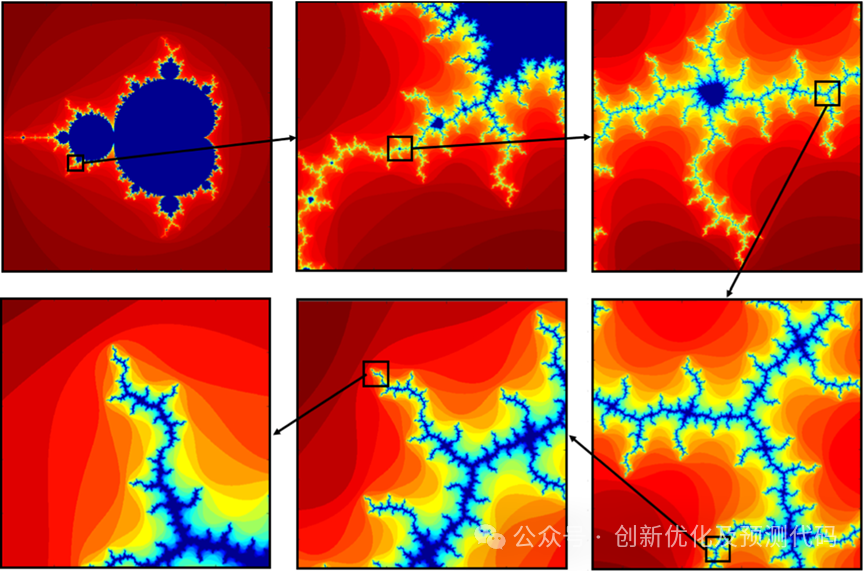
分形自相似性，用大白话说就是不管将某个图形放大多少倍，都能够在更复杂的局部中找到相似的图形，并且分型在我们的生活中无处不在，从银河系到海螺都能看到分形的影子。

文章介绍了用混沌博弈的方法逐步创建谢尔宾斯基三角形的过程。这些决策变量表示这些符合条件的种子在谢尔宾斯基三角形中的位置。谢尔宾斯基三角形被认为是优化算法中候选解的搜索空间。对于搜索空间中的每个初始合格种子，都会创建一个临时三角形，目的是在搜索空间内创建一些新的种子，这些种子可以被视为完成谢尔宾斯基三角形的新合格种子，用于完成谢尔宾斯基三角形的整体形状。

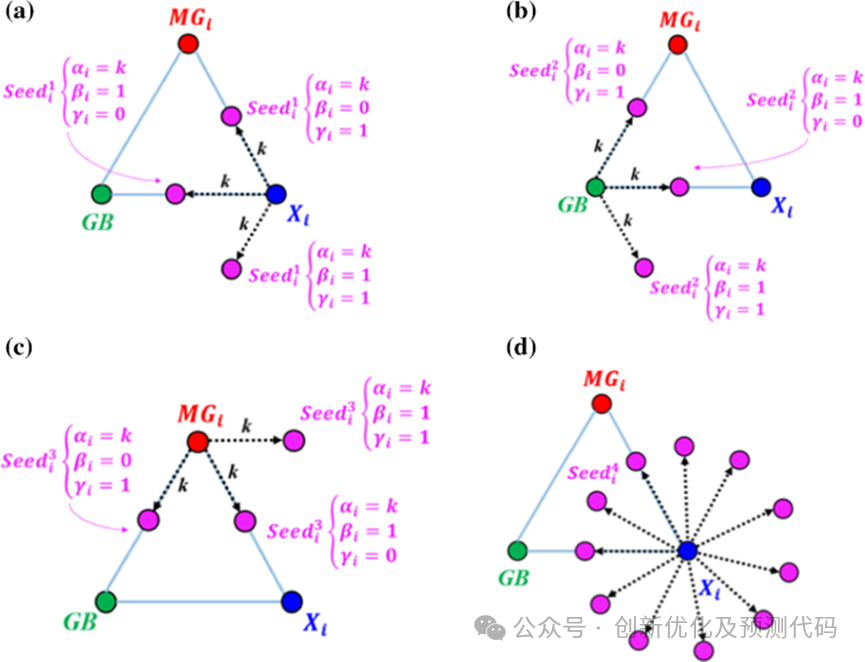
构成的CGO-CNN-BiGRU-Attention多变量回归预测模型的创新性在于以下几点：

CGO算法区别于传统智能算法的创新性：

①无参数框架：CGO算法是一种无参数的元启发式方法，在整个优化过程中不需要定义任何内部参数，换句话说，减少了人为设定参数带来的误差。

②物理概念明确：引入了混沌理论，又考虑了分形的合格构型和分形自相似性问题，其中搜索空间的全局和局部搜索以更灵敏的方式得到满足。这种基于物理学的方法使得CGO算法在全局优化问题上具有更好的可解释性。

③对比其他优化算法的优越性：通过与其他随机优化算法进行对比实验，CGO算法在收敛性和统计数据方面表现出色。实验结果表明，CGO算法在多个基准问题上优于其他比较算法。这表明CGO算法在解决优化问题时具有更高的效果和性能。

优化套用—基于混沌博弈优化算法（CGO）、卷积神经网络（CNN）和双向门控循环单元网络(BiGRU)融合注意力机制（SelfAttention）的超前24步多变量时间序列回归预测算法CGO-CNN-BiGRU-Attention：

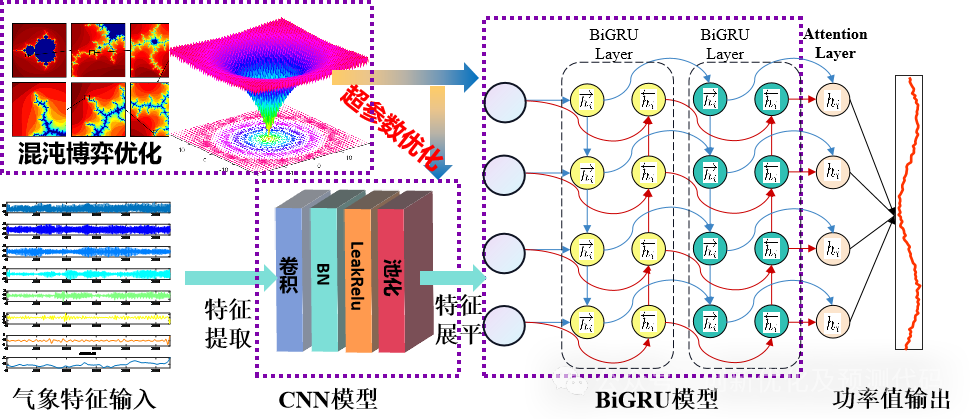
功能：

1、多变量特征输入，单序列变量输出，输入前一天的特征，实现后一天的预测，超前24步预测。

2、通过CGO优化算法优化学习率、卷积核大小、神经元个数，这3个关键参数，以最小MAPE为目标函数。

3、提供损失、RMSE迭代变化极坐标图；网络的特征可视化图；测试对比图；适应度曲线（若首轮精度最高，则适应度曲线为水平直线）。

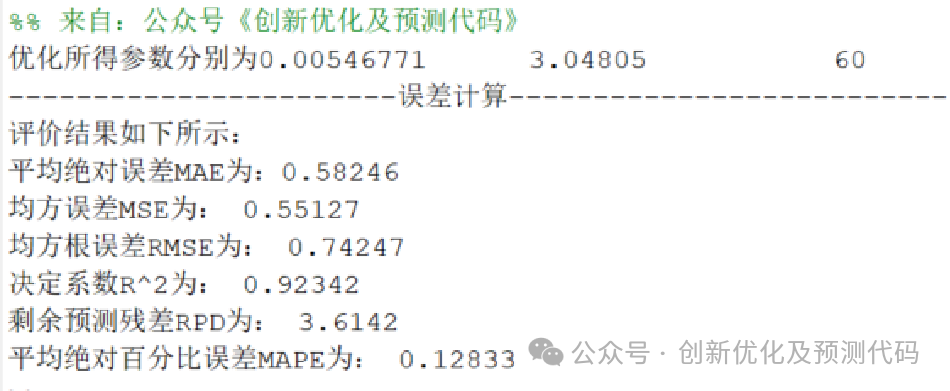
4、提供MAPE、RMSE、MAE等计算结果展示。

适用领域：风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。

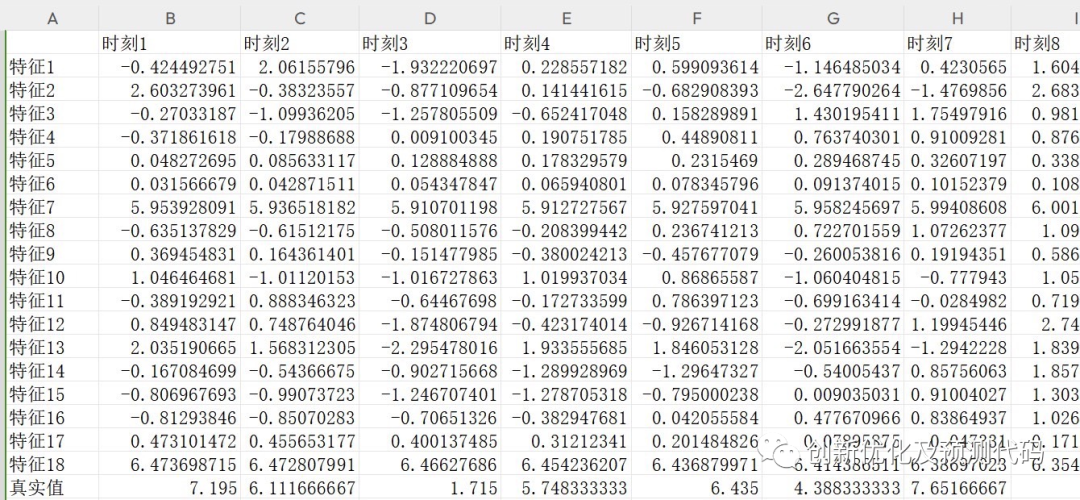
数据集格式：

前一天18个气象特征，采样时间为24小时，输出为第二天的24小时的功率出力，也就是18×24输入，1×24输出，一共有75个这样的样本。

预测值与实际值对比；训练特征可视化：

训练误差曲线的极坐标形式（误差由内到外越来越接近0）；适应度曲线（误差逐渐下降）

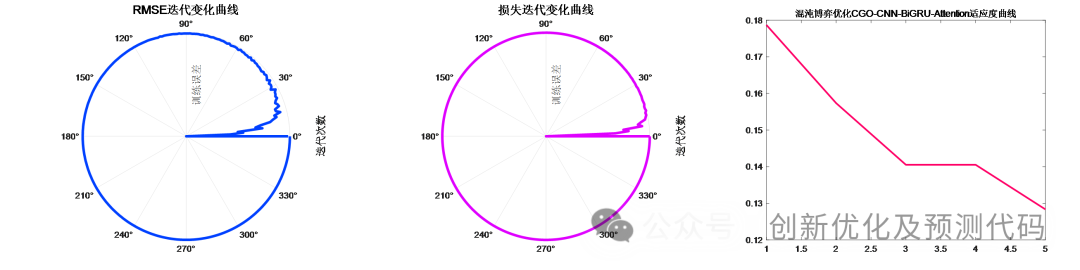
误差评估：

CGO部分核心代码：

% 来自公众号《创新优化及预测代码》function [BestFitness, BestSeed, Conv_History, bestPred, bestNet, bestInfo] = CGO(Seed_Number, MaxIter, lb, ub, dim, fobj)?%% 初始化for i = 1:Seed_Number    % 初始化初始可行点的位置   % 来自公众号《创新优化及预测代码》    Seed(i, :) = unifrnd(lb, ub);    % 初始化初始可行点的适应度  % 来自公众号《创新优化及预测代码》    [Fun_eval(i, 1), Pred{i, 1}, Net{i, 1}, Info{i, 1}] = feval(fobj, Seed(i, :));end%% CGO 的搜索过程  % 来自公众号《创新优化及预测代码》for Iter = 1:MaxIter    for i = 1:Seed_Number        % 更新最佳种子          [~, idbest] = min(Fun_eval);        BestSeed = Seed(idbest, :);        bestPred = Pred{idbest, :};        bestNet = Net{idbest, :};        bestInfo = Info{idbest, :};        %% 生成新的解决方案  % 来自公众号《创新优化及预测代码》        % 随机数        I = randi([1, 2], 1, 12); % Beta 和 Gamma        Ir = randi([0, 1], 1, 5);        % 随机组        RandGroupNumber = randperm(Seed_Number, 1);        RandGroup = randperm(Seed_Number, RandGroupNumber);        % 随机组的平均值  % 来自公众号《创新优化及预测代码》        MeanGroup = mean(Seed(RandGroup, :)) .* (length(RandGroup) ~= 1) ...            + Seed(RandGroup(1, 1), :) * (length(RandGroup) == 1);        % 新的种子        Alfa(1, :) = rand(1, dim);        Alfa(2, :) = 2 * rand(1, dim) - 1;        Alfa(3, :) = (Ir(1) * rand(1, dim) + 1);        Alfa(4, :) = (Ir(2) * rand(1, dim) + (~Ir(2)));        ii = randi([1, 4], 1, 3);        SelectedAlfa = Alfa(ii, :);?        NewSeed(1, :) = Seed(i, :) + SelectedAlfa(1, :) .* (I(1) * BestSeed - I(2) * MeanGroup);        NewSeed(2, :) = BestSeed + SelectedAlfa(2, :) .* (I(3) * MeanGroup - I(4) * Seed(i, :));        NewSeed(3, :) = MeanGroup + SelectedAlfa(3, :) .* (I(5) * BestSeed - I(6) * Seed(i, :));        NewSeed(4, :) = unifrnd(lb, ub);        for j = 1:4            % 检查/更新种子的边界限制  % 来自公众号《创新优化及预测代码》            NewSeed(j, :) = bound(NewSeed(j, :), ub, lb);            % 评估新的解决方案   % 来自公众号《创新优化及预测代码》            [Fun_evalNew(j, :), PredNew{j, 1}, NetNew{j, 1}, InfoNew{j, 1}] = feval(fobj, NewSeed(j, :));        end        Seed = [Seed; NewSeed];        Pred = [Pred; PredNew];        Net = [Net; NetNew];        Info = [Info; InfoNew];        Fun_eval = [Fun_eval; Fun_evalNew];    end

部分图片来源于网络，侵权联系删除！

关注小编会不定期推送高创新型、高质量的学习资料、文章程序代码，为你的科研加油助力!