Ring Co-XOR encryption based reversible data hiding for 3D mesh model

期刊：Signal Processing

作者：Lingfeng Qu et al.

--

摘要：

加密域可逆数据隐藏被广泛应用于云存储数字媒体的内容安全、隐私保护和便捷管理。然而，RDH-ED技术在三维网格模型载体中的应用研究仍处于起步阶段。为解决现有针对三维网格模型的RDH-ED算法需要像第三方传输辅助信息，嵌入容量不高等问题，本文提出一种基于环的协同异或加密(RCXOR)的可逆数据隐藏方案。首先，将原始3D网格模型划分为互不重叠的环，不同的环不存在共享顶点。接着，对同一个环中的顶点用相同的随机数按位异或加密，以保留加密后环中相邻顶点的冗余。最后，基于RCXOR加密提出一种基于环心顶点的多MSB预测方法，环心顶点作为参考顶点预测环边顶点的多个MSB腾出房间用于数据隐藏，采用范式霍夫曼编码压缩标签获得最优嵌入容量。实验结果表明，提出算法与最先进算法相比具有较高的安全性和嵌入容量。

引言（简介）：

这里对原文中引言以及相关工作部分做总结与简介，与原文不一致。

3D网格模型是一种新型的载体，被广泛应用于医疗器官制作、建筑结构展示、机械制图、动画制作等领域。如何将基于图像的RDH技术应用到3D网格模型载体中已成为领域的研究热点。现有针对3D网格模型的RDH技术可以被划分为三类：空间域、变换域、压缩域。

基于空域的RDH技术通过修改魔性的顶点坐标来嵌入数据。Wu等人[]通过条件网格的面和质心的距离在模型中可逆的嵌入脆弱水印，实现对3D网格模型的认证。In [],? Wu等人将PEE技术应用到3D网格模型的顶点中，实现在网格模型中可逆的潜入数据。Zhang等人[]采用环形模式来预测顶点位置提高了预测精度，通过PEE和排序方法使得算法在增强容量和降低失真方面取得了更好的性能。Jiang等人[]基于最优三维预测误差直方图(PEH)修正和递归结构编码(RCC)方法进一步提升了3D网格RDH的嵌入容量和恢复质量。Girdhar等人基于DE思想在3D网格模型中使用混沌映射来隐藏秘密信息，在嵌入容量和视觉质量方面取得了较好的效果。第二类是将秘密数据隐藏在3D模型的频域中，Luo等人[]用随机选择的种子顶点创建一组8个相邻顶点的集群，利用3D网格模型顶点间的强相关性将秘密数据隐藏在集群中的DCT域中。第三类是基于压缩域的RDH技术[]，这类方法将网格模型无损压缩后腾出空间，在模型中可逆的嵌入秘密数据。

上述方法都是直接在原始3D网格模型中隐藏秘密数据而不能保护模型的内容信息。随着云计算和大数据等技术的发展， 3D网格模型等各种数字媒体可以保存在私有、公有和混合等开放或半开放云环境中[1]。对云存储数字图像的内容安全、隐私保护和便捷管理等需求，推动着图像加密域可逆信息隐藏(RDH-ED: Revisable Data Hiding in Encrypted domain)技术的发展。现有RDH-ED技术可以被划分类两大类：Vacating room after encryption（VRAE：）和Vacating room after encryption(VRBE)。VRBE框架的RDH-ED算法利用原始媒体内容的冗余预留空间后再对媒体进行加密，能够获得较高的嵌入容量。Ma等人[25]提出了第一个VRBE算法，该算法使用传统的RDH算法[4]将图像部分像素的LSB嵌入到更平滑的区域，从而为信息隐藏预留空间，该方法在嵌入容量方面取得了较好的效果。近年来，研究者们已经将VRBE框架引用到3D网格模型中，Xu等人[]利用3D网格模型相邻顶点间的相关性，提出一种基于顶点MSB预测和整数映射的REH-ED方法，该方法获得了较高的嵌入容量。为进一步提升嵌入容量，Yin等人[]将[]种的MSB预测扩展为多MSB预测，获得更高的嵌入容量，不过，算法顶点利用率不高。最近, Lv等人[]通过将顶点按索引划分为奇数顶点和偶数顶点。用偶数顶点预测奇数顶点的多MSB，顶点利用率达到50%，且一个可嵌入顶点能潜入多比特数据，在数据集上的平均嵌入率达到25.65bpv。不过，对于VRBE框架的RDH-ED算法，一方面对原始载体的预处理会增加了内容拥有者的计算负担，更重要的是为保证算法的可逆性，预留空间的过程中往往会产生附加数据，对附加数据的处理可能会带来一些安全隐患。

?不同于VRBE框架，基于VRAE框架下的RDH-ED算法直接在加密后的载体中嵌入秘密数据。 由于用户只需要对载体做加密处理而不需要预处理，且不需要向第三方传输辅助数据，能降低用户的计算负担。不过，由于加密使得原始载体的冗余降低，算法的嵌入容量或恢复质量受到限制。In 2017, Jiang等人[]首次提出基于3D网格模型流密码异或加密的RDH-ED算法。算法将异或加密后的顶点划分为嵌入集和参考集，通过翻转嵌入集中顶点的LSB位实现1比特数据的嵌入，该算法的嵌入容量较低且数据提取可能存在误差。Shah等人[]利用同态加密的特性在加密后的模型中嵌入数据，提升了嵌入容量。在[]中，一种新的基于Paillier加密的3D网格模型RDH方法被提出，双层嵌入的策略使得该算法嵌入容量进一步提升，通过控制坐标的加密位长，避免了数据的扩展。但是，同态加密会导致数据的扩展，且同态加密算法时间复杂度较高。同态加密虽然具有较高的安全性，不过算法的时间复杂度较高，不适用于对大量数据加密的应用场景。Tsai[37]采用流密码加密对3D网格模型加密后，提出了一种基于空间细分和空间编码的可分离可逆数据隐藏方法。该算法具有较高的保密性，可实现可分离可逆数据隐藏，计算复杂度低，嵌入容量大，失真可控等优点。为进一步提升VRAE框架下3D网格模型RDH-ED算法的嵌入容量，本文设计一种3D网格模型的环协同异或加密的多MSB预测算法，主要贡献如下：??

1）提出一种新的环-协同异或加密方法。通过将3D网格模型划分为互不重叠的环， 对同一个环采用相同的一组随机比特按位异或加密以保留同一个环中相邻顶点间的冗余。

2）提出基于环心顶点的多MSB预测方法。由于RCXOR加密后的模型中不同的环不存在共享顶点，将环心顶点作为参考顶点，用环心顶点预测多个环边顶点的多MSB位实现在环边顶点的多MSB腾出空间。

3）采用范式霍夫曼编码的方法有效压缩标签进一步提升算法的嵌入容量。实验结果表明，提出算法的嵌入容量与现有VRAE和VRBE框架下的RDH-ED算法相比都存在优势。

本文以最常用三角形网格模型为研究对象，该模型是由若干三角形组成的三维立体图像。三维网格图像有着不同的储存格式，例如OFF,OBJ,MD2,etc,我们以OFF格式的3D图像为例介绍本文算法。三维网格图像的存储主要由两个重要参数集组成，分别是顶点集 ， ， 为顶点的个数，和表面集 ， , 为面的个数。对于三角形模型而言，三个顶点可以构成一个面。未压缩3D网格模型的顶点坐标表示为32位浮点数，但有效位只有6位。Deering等人建议，大多数3D模型的应用在一个可接受的精度水平上执行即可，而不需要对每个浮点坐标进行操作。对顶点的归一化操作与之前的文献一样。

内容所有者对三维网格模型的顶点预处理后，基于加密秘钥 对顶点坐标实现环形共异或加密。三维网格模型中相邻坐标顶点具有较高的相关性，RCXOR加密能更好地保留相邻顶点坐标间的相关性，从而获得更高的嵌入容量。我们将三维网格顶点划分为不重叠的环，对于相同环内的顶点采用相同的随机数进行异或加密，以保留相邻顶点坐标高位平面的冗余。RCXOR加密主要包含两个步骤：1）顶点划分，2）顶点CXOR加密。

加密方法

1）顶点划分

由于三维网格图像中，相邻顶点间包含了多个三角形，即一个顶点会被多个三角形共享。我们需要对原始三维网格模型 中的顶点划分成 ? 个不重叠的环。

对原始三维网格图像 , ， ，这里， 为 中第 个环， ，其中， 为一个环中环边顶点的总个数。 为环 的环心顶点， 为环边顶点。一个环由一个环心顶点 和 个环边顶点 构成。我们给出 中环的定义：? ???

定义1：将 中的所有顶点按索引分为偶数索引和奇数两类，奇数（偶数）索引顶点作为环心，与其相连的偶数（奇数）索引顶点作为环边，环心与环边共同构成一个环。不同的环中不存在共享顶点，即对于任意两个环必定满足： 。

我们以图2为例介绍环的划分过程。图2（a）为Mushroom的三维网格模型，图2（b）为（a）中的红色区域。图2（b）中用不同颜色表示了每个顶点的索引，其中，红色点为奇数索引，蓝色点为偶数索引。我们选取奇数索引顶点作为一个环的环心，偶数索引顶点作为环边。图2（b）中共有两个环，环心索引为3的环我们称作环1， 。环心索引为13的环称为环2 。索引为4的顶点被两个环分享，按照环的定义，我们将顶点4分配给索引距离最近的奇数顶点? ，因此，环2为 。

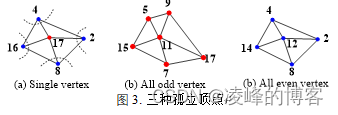
对任意的三维网格模型，我们将无法与周围的顶点构成一个环的顶点称为孤立顶点。三维网格模型中除了环之外还存在少量的孤立顶点，孤立顶点可以被分为以下三种类型：

1）Single vertex。环心索引为奇数，周围所有的偶数顶点都与别的环心共享，且周围所有偶数顶点都分配给别的环心。

2）All old vetex。环心为奇数且与之相连的所有顶点均为奇数。

3）All even vetex。环心为偶数且与之相连的所有顶点均为偶数。

??图3为三种孤立顶点示例，其中图3（a）为单顶点，环心为奇数索引17，周围四个偶数索引顶点均被分配给其余的环心。图3（b）为全奇数顶点，环心为奇数索引11，与之相连的顶点均为奇数索引。图3(c)为全偶数索引，环心为偶数索引12，与之相连的索引均为偶数。为保证算法的可逆性，三种类型的孤立顶点均不能用于数据嵌入。

2）环异或加密

内容拥有者基于加密秘钥? 生成 组不同的二进制随机序列 ,其中， 为环的总个数， 为孤立顶点的个数。 , 为顶点坐标的二进制位长度， 。

按照环心的索引顺序，将每个环中的顶点转换为二进制比特。对任意环 ，? 为环中顶点的总个数，以环边顶点为例， 中每个顶点坐标的二进制形表示为 ,这里 , ?

?? (4)

其中， 为归一化后的顶点， 为向下取整函数，对于任意环 。将二进制随机序列 与环中所有顶点的二进制序列按位异或加密。

? ?? ??? (5)

为加密后的二进制比特， 为按位异或操作。归一化后顶点的高比特位经常为连续的0，由于高位比特被随机数异或加密，加密后的顶点值会被再次扩大，为了便于显示，最终的加密顶点需要缩小 倍，这个过程不会丢失顶点的精度。三维网格模型中，任意环中的加密顶点 可以通过式（6）计算的得到， ?

?????????? (6)

同一个环中的顶点与相同的一组随机二进制比特按位异或加密，不同的环之间异或加密所用的随机二进制比特不同。对于每个孤立顶点，单独使用一组随机二进制比特对孤立顶点按位异或加密。RCXOR加密后的三维网格模型为 ， , 。RCXOR加密只改变顶点坐标的值，而不改变顶点之间的拓扑结构以及顶点坐标的符号。

基于多MSB预测的信息隐藏 ?

由于加密过程不改变三维模型顶点间的拓扑结构，信息隐藏者通过扫描加密模型 E 的顶点即可区分加密模型中的环和孤立顶点，从而可以将秘密信息隐藏到加密顶点中，对孤立顶点不隐藏任何信息。本节首先对RCXOR加密的三维网格提出一种基于环的MSB预测方法，接着，在加密的三维网格图像中实现可逆信息嵌入。

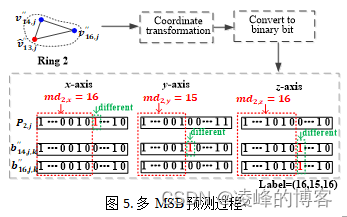
1）环的多MSB预测

本节提出一种基于环的多MSB预测方法在加密的3D模型中腾出空间用于信息隐藏。由RCXOR加密过程可知，对一个3D模型所有环心顶点，可能存在一些孤立顶点，这些环心顶点由于周围没有任何顶点用于参考，因此不能用于信息隐藏。 对于非孤立顶点的环心，不同的环中不存在共享顶点，且同一个环中的环心顶点与环边顶点存在较多的冗余，这些特点使得在加密3D网格中腾出空间提供了可能。

加密效果图：

第一行原始模型，第二行为RCXOR加密模型，第三行为含密-加密模型，第四行为恢复模型。

结论：

为解决现有3D网格模型加密需要传输辅助信息的问题，本文提出一种基于环协同异或加密的3D网格模型加密域可逆信息隐藏。首先将原始3D网格模型划分为互不重叠的环，不同的环不存在共享顶点，对同一个环中的顶点用相同的随机数加密以保留环中相邻顶点间的冗余。接着，提出一种基于环心顶点的多MSB预测方法在环边顶点的多个MSB中腾出空间用于数据隐藏，采用范式霍夫曼编码方法对生成的标签压缩以最大化算法的嵌入容量。实验结果表明提出的算法与现有VRAE框架下的加密3D网格模型可逆数据隐藏相比，嵌入容量有明显提升。对于VRBE框架下的加密3D网格模型可逆数据隐藏算法相比，嵌入容量也存在一定的优势。