代码随想录day30 回溯算法最终章

51. N皇后

题目

n?皇后问题 研究的是如何将 n?个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的?n?皇后问题 的解决方案。

每一种解法包含一个不同的?n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

• 输入：n = 4
• 输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
• 解释：如上图所示，4 皇后问题存在两个不同的解法。

思考

看到题就懵了，感觉和之前做的回溯算法完全不一样，这是真的开放性的题，开了卡哥的视频大概梳理出来了一些思路：

1、要创建的结果数组是三维的，因为棋盘是二维的，要存放棋盘

2、因为棋盘是n*n的，那么当纵向递归遍历到n时，收获结果

3、单层递归其实没啥难度，主要是判断当满足题意三个条件时才能纵向递归，注意这里要因为是在二维数组里递归，那么横向遍历的i和纵向递归遍历其实没啥关系，不用startIndex，直接row+1即可

4、满足的三个条件怎么写：

• 不能同一列出现两个Q，即col不变，判断从0到row的所有数是否有Q
• 不能45度出现Q，即3，3到2，2到1，1或者3，2到2，1不能出出现Q，row-1，col-1即可
• 不能135度出现Q，出3，3到2，4到1，5不能出现Q，row-1，col+1即可

代码

class Solution {

public:

? ? vector<vector<string>> res;

? ? void backTracking(vector<string>& chess, int n, int row){

? ? ? ? if(row == n) {

? ? ? ? ? ? res.push_back(chess);

? ? ? ? ? ? return;

? ? ? ? }

? ? ? ? for(int col = 0; col < n; col++) {

? ? ? ? ? ? if(isValid(row, col, chess, n)){

? ? ? ? ? ? ? ? chess[row][col] = 'Q';

? ? ? ? ? ? ? ? backTracking(chess, n, row+1);

? ? ? ? ? ? ? ? chess[row][col] = '.';

? ? ? ? ? ? }

? ? ? ? }

? ? }

? ? bool isValid(int row, int col, vector<string> chess, int n ) {

? ? ? ? for(int i = 0; i < row; i++) {

? ? ? ? ? ? if(chess[i][col] == 'Q') return false;

? ? ? ? }

? ? ? ? for(int i = row-1, j = col-1; i>=0 && j>=0; i--&j--) {

? ? ? ? ? ? if(chess[i][j]== 'Q') return false;

? ? ? ? }

? ? ? ? for(int i = row -1, j = col+1; i>=0 && j<n; i-- && j++) {

? ? ? ? ? ? if(chess[i][j] == 'Q') return false;

? ? ? ? }

? ? ? ? return true;

? ? }

? ? vector<vector<string>> solveNQueens(int n) {

? ? ? ? vector<string> chess(n, string(n, '.'));

? ? ? ? backTracking(chess, n, 0);

? ? ? ? return res;

? ? }

};

37. 解数独

题目

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则： 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。

一个数独。

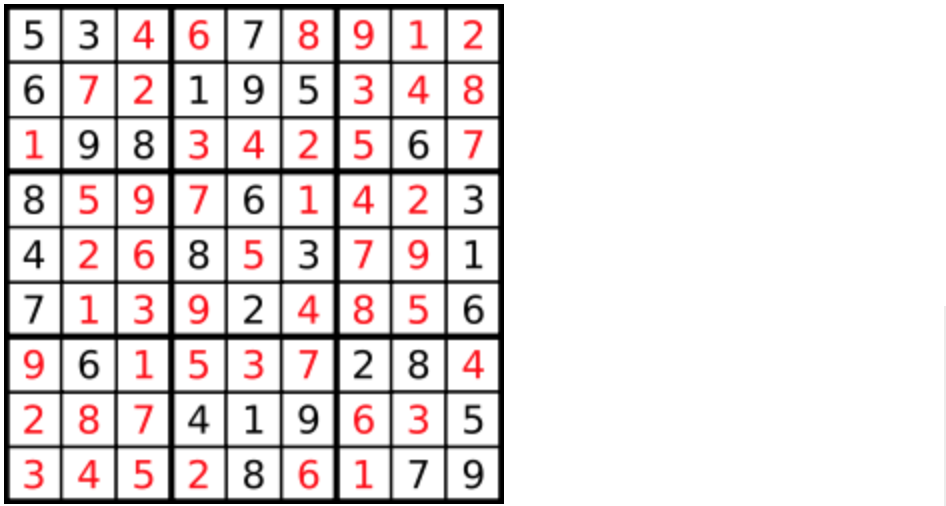
答案被标成红色。

提示：

• 给定的数独序列只包含数字 1-9 和字符 '.' 。
• 你可以假设给定的数独只有唯一解。
• 给定数独永远是 9x9 形式的。

思考

太难了，感觉和n皇后是差不多的，也是三个条件，但是具体应该怎么写完全一头雾水，看完卡哥视频稍微总结一下吧：

1. 上来不是void函数，是bool类型的，直接遍历，i<9,j<9
2. 当board[i][j] =='.'时，说明需要填充数字，开始循环判断1-9中哪个数字满足条件，如果满足，直接填上
3. 注意，这里的中止条件竟然在填充完数字后，如果填充了，那么判断整个函数是否为true，如果为true，返回true
4. 如果1-9中数字不满足条件，那么要return false
5. 三个条件写法

• 纵向判断要填充的数字是否已经在那一列里
• 横向判断要填充的数字是否已经在那一行里
• 在3*3的九宫格里判断要填充的数字是否在九宫格里，用两个for循环，并且startRow和StartCol需要用（row/3）*3来表示

代码

class Solution {

private:

? ? bool backTracking(vector<vector<char>>& board) {

? ? ? ? for(int i = 0; i < board.size(); i++) {

? ? ? ? ? ? for(int j = 0; j < board.size(); j++) {

? ? ? ? ? ? ? ? if(board[i][j] == '.') {

? ? ? ? ? ? ? ? ? ? for(char k = '1'; k <= '9'; k++) {

? ? ? ? ? ? ? ? ? ? ? ? if(isValid(i, j, k, board)) {

? ? ? ? ? ? ? ? ? ? ? ? ? ? board[i][j] = k;

? ? ? ? ? ? ? ? ? ? ? ? ? ? bool tmp = backTracking(board);

? ? ? ? ? ? ? ? ? ? ? ? ? ? if(tmp) return true;

? ? ? ? ? ? ? ? ? ? ? ? ? ? board[i][j] = '.';

? ? ? ? ? ? ? ? ? ? ? ? }

? ? ? ? ? ? ? ? ? ? }

? ? ? ? ? ? ? ? ? ? return false;

? ? ? ? ? ? ? ? }

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? return true;

? ? }

? ? bool isValid(int row, int col, char val, vector<vector<char>>& board) {

? ? ? ? for(int i = 0; i < 9; i++) {

? ? ? ? ? ? if(board[row][i] == val) return false;

? ? ? ? }

? ? ? ? for(int j = 0; j < 9; j++) {

? ? ? ? ? ? if(board[j][col] == val) return false;

? ? ? ? }

? ? ? ? int startRow = (row/3) * 3;

? ? ? ? int startCol = (col/3) * 3;

? ? ? ? for(int i = startRow; i < startRow+3; i++) {

? ? ? ? ? ? for(int j = startCol; j < startCol+3; j++) {

? ? ? ? ? ? ? ? if(board[i][j] == val) return false;

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? return true;

? ? }

public:

? ? void solveSudoku(vector<vector<char>>& board) {

? ? ? ? backTracking(board);

? ? }

};