UCB Data100:数据科学的原理和技巧:第十六章到第十八章
十六、交叉验证和正则化
Cross Validation and Regularization
译者:飞龙
学习成果
-
认识到需要验证和测试集来预览模型在未知数据上的表现
-
应用交叉验证来选择模型超参数
-
了解 L1 和 L2 正则化的概念基础
在特征工程讲座结束时(第 14 讲),我们提出了调整模型复杂度的问题。我们发现一个过于复杂的模型会导致过拟合,而一个过于简单的模型会导致欠拟合。这带来了一个自然的问题:我们如何控制模型复杂度以避免欠拟合和过拟合?
为了回答这个问题,我们需要解决两件事:首先,我们需要通过评估模型在未知数据上的表现来了解何时我们的模型开始过拟合。我们可以通过交叉验证来实现这一点。其次,我们需要引入一种调整模型复杂度的技术 - 为此,我们将应用正则化。
16.1 训练、测试和验证集
从上一讲中,我们了解到增加模型复杂度减少了模型的训练误差,但增加了它的方差。这是很直观的:添加更多的特征使我们的模型更紧密地拟合了训练过程中遇到的数据,但对新数据的泛化能力更差。因此,低训练误差并不总是代表我们模型的基本性能 - 我们还需要评估它在未知数据上的表现,以确保它没有过拟合。
事实上,唯一知道我们的模型何时过拟合的方法是在未知数据上评估它。不幸的是,这意味着我们需要等待更多的数据。这可能非常昂贵和耗时。
我们应该如何进行?在本节中,我们将建立一个可行的解决方案来解决这个问题。
16.1.1 测试集
避免过拟合的最简单方法是将一些数据“保密”不让自己知道。我们可以将完整数据集的随机部分保留下来,仅用于测试目的。这个测试集中的数据点不会用于模型拟合过程。相反,我们将:
-
使用我们数据集的剩余部分 - 现在称为训练集 - 运行普通最小二乘法、梯度下降或其他一些技术来拟合模型参数
-
拿到拟合的模型并用它对测试集中的数据点进行预测。模型在测试集上的表现(以 MSE、RMSE 等表示)现在表明了它在未知数据上的预测能力有多好
重要的是,最佳模型参数是通过仅考虑训练集中的数据找到的。在模型拟合到训练数据之后,我们在进行测试集上的预测之前不改变任何参数。重要的是,我们在最终确定所有模型设计后,只对测试集进行一次预测。我们将测试集的表现视为模型表现的最终测试。
将我们的数据集分成训练集和测试集的过程被称为训练-测试拆分。通常,10%到 20%的数据被分配给测试集。

在sklearn中,model_selection模块的train_test_split函数允许我们自动生成训练-测试拆分。
在今天的工作中,我们将继续使用之前讲座中的vehicles数据集。与以往一样,我们将尝试从hp的转换中预测车辆的mpg。在下面的单元格中,我们将完整数据集的 20%分配给测试,剩下的 80%分配给训练。
代码
import pandas as pd
import numpy as np
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
# Load the dataset and construct the design matrix
vehicles = sns.load_dataset("mpg").rename(columns={"horsepower":"hp"}).dropna()
X = vehicles[["hp"]]
X["hp^2"] = vehicles["hp"]**2
X["hp^3"] = vehicles["hp"]**3
X["hp^4"] = vehicles["hp"]**4
Y = vehicles["mpg"]
from sklearn.model_selection import train_test_split
# `test_size` specifies the proportion of the full dataset that should be allocated to testing
# `random_state` makes our results reproducible for educational purposes
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=220)
print(f"Size of full dataset: {X.shape[0]} points")
print(f"Size of training set: {X_train.shape[0]} points")
print(f"Size of test set: {X_test.shape[0]} points")
Size of full dataset: 392 points
Size of training set: 313 points
Size of test set: 79 points
在进行训练-测试拆分后,我们将模型拟合到训练集,并评估其在测试集上的表现。
import sklearn.linear_model as lm
from sklearn.metrics import mean_squared_error
model = lm.LinearRegression()
# Fit to the training set
model.fit(X_train, Y_train)
# Make predictions on the test set
test_predictions = model.predict(X_test)
16.1.2 验证集
现在,如果我们对测试集的性能不满意怎么办?按照我们目前的框架,我们就会陷入困境。如前所述,评估模型在测试集上的性能是模型设计过程的最终阶段。我们不能回头根据新发现的过拟合来调整模型 - 如果这样做,我们就会考虑测试集的信息来设计我们的模型。测试误差将不再是模型在未见数据上性能的真实代表!
我们的解决方案是引入一个验证集。验证集是训练集的一个随机部分,用于在模型仍在开发中时评估模型性能。使用验证集的过程是:
-
进行训练-测试分割。将测试集放在一边;直到模型设计过程的最后才会使用。
-
设置一部分训练集用于验证。
-
将模型参数拟合到剩余训练集中包含的数据点。
-
评估模型在验证集上的性能。根据需要调整模型,重新拟合剩余部分的训练集,然后在验证集上重新评估。如有必要,重复此过程直到满意为止。
-
在所有模型开发完成后,评估模型在测试集上的性能。这是模型在未见数据上表现如何的最终测试。不应对模型进行进一步修改。
创建验证集的过程称为验证分割。

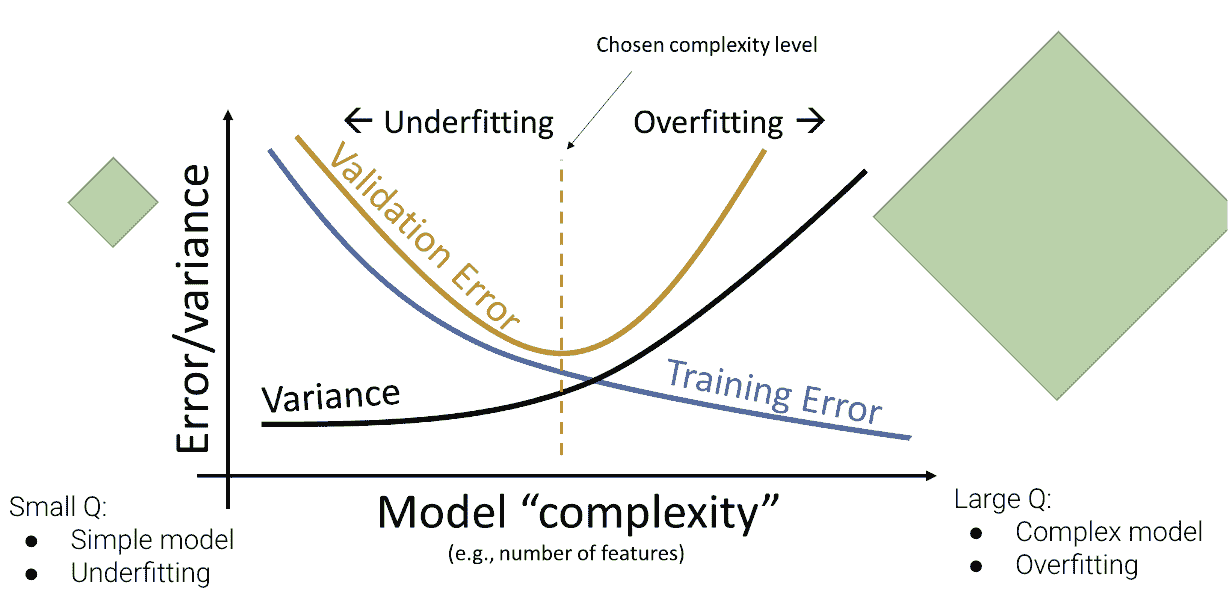
请注意,验证误差与之前探讨的训练误差行为有很大不同。回想一下,训练误差随着模型度数的增加而单调递减 - 随着模型变得更复杂,它在训练数据上做出了更好的预测。相反,验证误差在增加模型复杂度时先减少然后增加。这反映了从欠拟合到过拟合的转变。在低模型复杂度时,模型欠拟合,因为它不够复杂以捕捉数据的主要趋势。在高模型复杂度时,模型过拟合,因为它对训练数据进行了过于紧密的“记忆”。
我们可以更新我们对误差、复杂度和模型方差之间关系的理解:

我们的目标是训练一个复杂度接近橙色虚线的模型 - 这是我们的模型在验证集上达到最小误差的地方。请注意,这种关系是对现实世界的简化。但对于 Data 100 来说,这已经足够了。
16.2 K-Fold Cross-Validation
引入验证集给了我们一个“额外”的机会,评估模型在另一组未见数据上的性能。我们能够根据模型在这一组验证数据上的性能来微调模型设计。
但是,如果碰巧我们的验证集包含了很多异常值怎么办?可能我们设置的验证数据点实际上并不代表模型可能遇到的其他未见数据。理想情况下,我们希望在几个不同的未见数据集上验证模型的性能。这将让我们更加自信地了解模型在新数据上的行为。
让我们回顾一下我们的验证框架。之前,我们设置了训练数据的 x%(比如 20%)用于验证。

在上面的例子中,我们设置了前 20%的训练数据点作为验证集。这是一个任意的选择。我们可以将任何20%的训练数据用于验证。事实上,有 5 个不重叠的“块”训练数据点,我们可以指定为验证集。

其中一个这样的块的常见术语是折叠。在上面的示例中,我们有 5 个折叠,每个折叠包含 20%的训练数据。这给了我们一个新的视角:我们在我们的训练集中实际上有5个“隐藏”的验证集。
在交叉验证中,我们为训练集中的每个折叠执行验证拆分。对于具有 K K K个折叠的数据集,我们:
-
选择一个折叠作为验证折叠
-
将模型拟合到除验证折叠之外的每个折叠的训练数据
-
计算验证折叠上的模型误差并记录它
-
对所有 K K K个折叠重复
交叉验证误差然后是所有
K
K
K个验证折叠的平均误差。
16.2.1 模型选择工作流程
在这个阶段,我们已经完善了我们的模型选择工作流程。我们首先执行训练-测试拆分,以设置一个测试集,用于最终评估模型性能。然后,我们在调整设计矩阵和计算交叉验证误差之间交替,以微调模型的设计。在下面的示例中,我们说明了使用 4 折交叉验证来帮助确定模型设计。
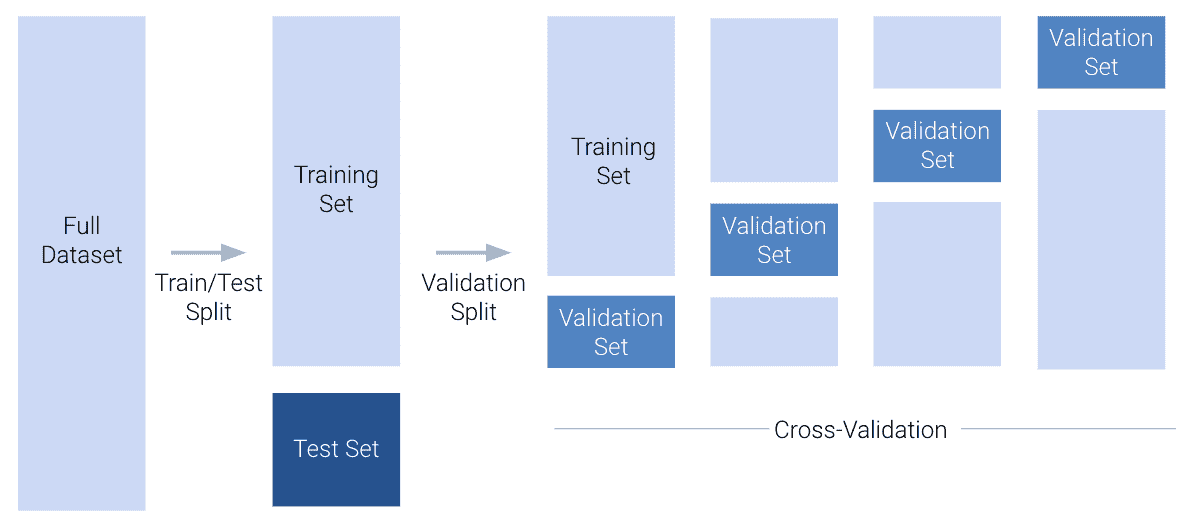
16.2.2 超参数
交叉验证的一个重要用途是进行超参数选择。超参数是模型中在模型拟合到任何数据之前选择的一些值。这意味着它与模型参数 θ i \theta_i θi?不同,因为它的值是在训练过程开始之前选择的。我们不能使用我们通常的技术 - 微积分、普通最小二乘法或梯度下降 - 来选择它的值。相反,我们必须自己决定。
Data 100 中一些超参数的例子是:
-
我们的多项式模型的程度(回想一下,在创建设计矩阵和调用
.fit之前我们选择了程度) -
梯度下降中的学习率 α \alpha α
-
正则化惩罚 λ \lambda λ(稍后将介绍)
为了通过交叉验证选择超参数值,我们首先列出了几个关于最佳超参数可能是什么的“猜测”。对于每个猜测,我们然后运行交叉验证,计算模型在使用该超参数值时产生的交叉验证误差。然后我们选择导致最低交叉验证误差的超参数值。
例如,我们可能希望使用交叉验证来决定我们应该使用什么值作为 α \alpha α,它控制每次梯度下降更新的步长。为此,我们列出了最佳 α \alpha α的一些可能猜测:0.1、1 和 10。对于每个可能的值,我们执行交叉验证,看当我们使用该 α \alpha α值来训练模型时,模型产生了什么错误。

16.3 正则化
我们现在已经解决了今天的两个目标中的第一个:创建一个框架来评估模型在未见数据上的性能。现在,我们将讨论我们的第二个目标:开发一种调整模型复杂性的技术。这将使我们能够直接解决欠拟合和过拟合的问题。
早些时候,我们通过调整超参数(多项式的程度)来调整多项式模型的复杂性。我们尝试了几个不同的多项式程度,计算了每个的验证误差,并选择了最小化验证误差的值。调整“复杂性”很简单;只需要调整多项式程度。
在大多数机器学习问题中,复杂性的定义与我们迄今为止所见的不同。今天,我们将探讨复杂性的两种不同定义: θ i \theta_i θi?系数的平方和绝对大小。
16.3.1 约束模型参数
回想一下我们使用梯度下降来下降损失曲面的工作。您可能会发现参考梯度下降笔记来提醒自己会很有帮助。我们的目标是找到导致模型损失最小的模型参数组合。我们通过在水平和垂直轴上绘制可能的参数值来使用等高线图来可视化这一点,这使我们可以从上方鸟瞰损失曲面。我们希望找到对应于损失曲面上最低点的模型参数。

让我们回顾一下我们当前的建模框架。
Y ^ = θ 0 + θ 1 ? 1 + θ 2 ? 2 + … + θ p ? p \hat{\mathbb{Y}} = \theta_0 + \theta_1 \phi_1 + \theta_2 \phi_2 + \ldots + \theta_p \phi_p Y^=θ0?+θ1??1?+θ2??2?+…+θp??p?
回想一下,我们用 ? i \phi_i ?i?表示我们的特征,以反映我们进行了特征工程的事实。
以前,我们通过限制模型中存在的特征的总数来限制模型的复杂性。我们一次只包括有限数量的多项式特征;所有其他多项式都被排除在模型之外。
如果我们不是完全删除特定特征,而是保留所有特征,并且每个特征只使用“一点点”,会怎么样?如果我们限制每个特征对预测的贡献量,我们仍然可以控制模型的复杂性,而无需手动确定应该删除多少个特征。
我们所说的“一点点”是什么意思?考虑某个参数 θ i \theta_i θi?接近或等于 0 的情况。那么,特征 ? i \phi_i ?i?几乎不会影响预测 - 特征的权重值如此之小,以至于它的存在并不会显著改变KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: \hat{\mathbb{Y}的值。如果我们限制每个参数 θ i \theta_i θi?的大小,我们就限制了特征 ? i \phi_i ?i?对模型的贡献。这会减少模型的复杂性。
在正则化中,我们通过对模型参数 θ i \theta_i θi?的大小设置限制来限制模型的复杂性。
这些限制看起来是什么样子?假设我们规定所有绝对参数值的总和不能大于某个数字 Q Q Q。换句话说:
∑ i = 1 p ∣ θ i ∣ ≤ Q \sum_{i=1}^p |\theta_i| \leq Q i=1∑p?∣θi?∣≤Q
其中 p p p是模型中参数的总数。您可以将这看作是我们为模型分配每个参数的大小的“预算”。如果模型为某些 θ i \theta_i θi?分配了一个较大的值,它可能必须为其他一些 θ j \theta_j θj?分配一个较小的值。这会增加特征 ? i \phi_i ?i?对预测的影响,同时减少特征 ? j \phi_j ?j?的影响。模型需要战略地分配参数权重 - 理想情况下,更“重要”的特征将获得更大的权重。
请注意,截距项 θ 0 \theta_0 θ0?不受此约束的影响。我们通常不对截距项进行正则化。
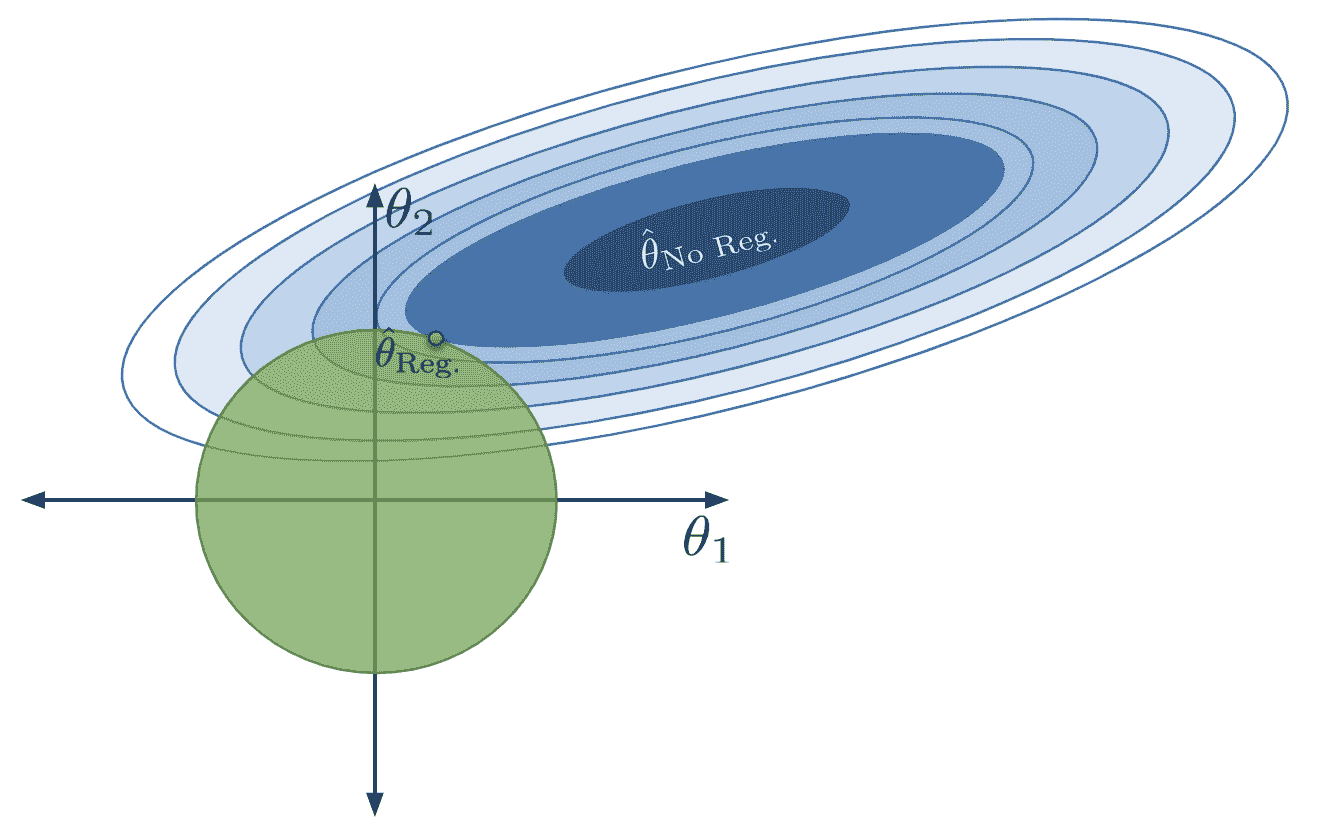
现在,让我们回想一下梯度下降,并将损失曲面可视化为等高线图。损失曲面表示每个点代表模型对 θ 1 \theta_1 θ1?、 θ 2 \theta_2 θ2?的特定组合的损失。假设我们的目标是找到使我们获得最低损失的参数组合。
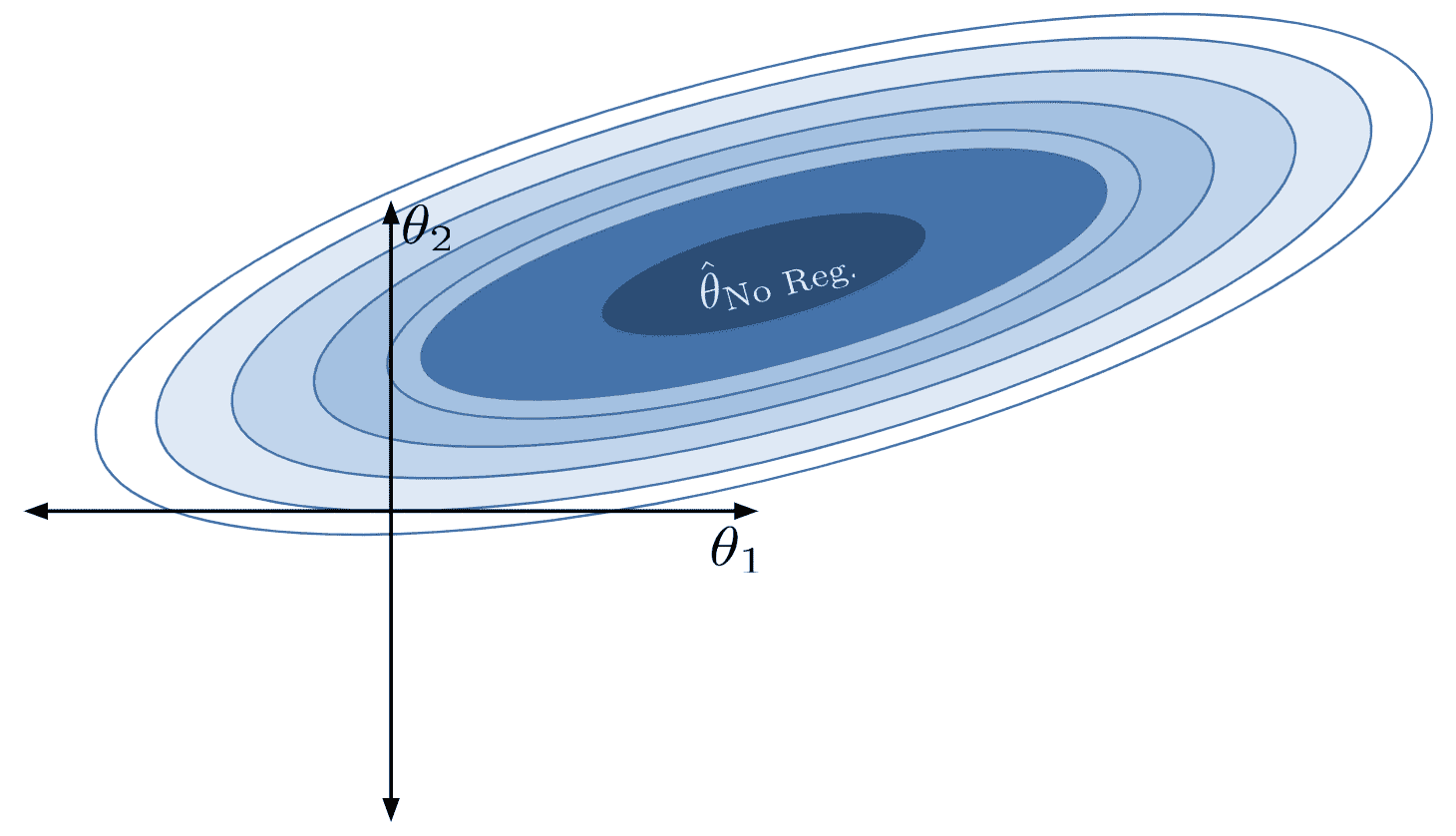
在没有约束的情况下,最优的 θ ^ \hat{\theta} θ^位于中心。
应用这个约束限制了模型参数的有效组合。现在我们只能考虑总绝对和小于或等于我们的数字 Q Q Q的参数组合。这意味着我们只能将我们的正则化参数向量 θ ^ Reg \hat{\theta}_{\text{Reg}} θ^Reg?分配到下面绿色菱形中的位置。

我们不能再选择真正最小化损失曲面的参数向量 θ ^ No?Reg \hat{\theta}_{\text{No Reg}} θ^No?Reg?,因为这组参数不在我们允许的区域内。相反,我们选择任何允许的组合,使我们尽可能接近真正的最小损失。
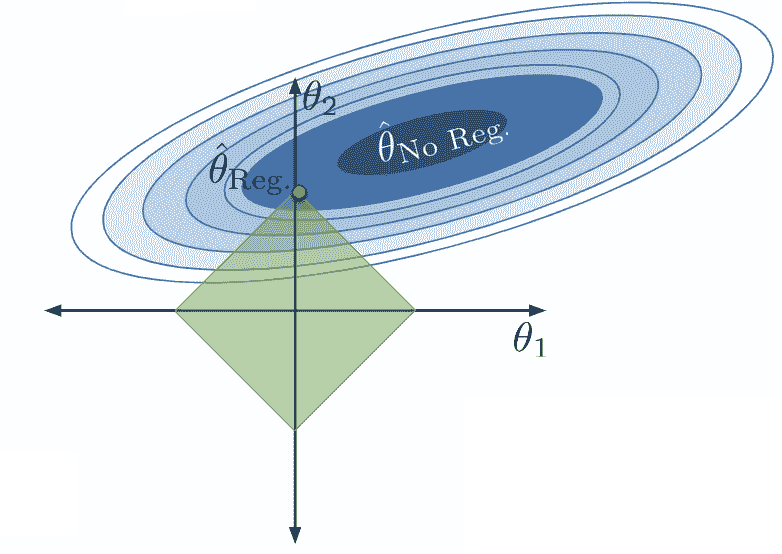
请注意,在正则化下,我们优化的 θ 1 \theta_1 θ1?和 θ 2 \theta_2 θ2?的值要比没有正则化时小得多(确实, θ 1 \theta_1 θ1?已经减少到 0)。模型的复杂度降低,因为我们限制了特征对模型的贡献。事实上,通过将其参数设置为 0,我们有效地从模型中完全删除了特征 ? 1 \phi_1 ?1?的影响。
如果我们改变 Q Q Q的值,我们就改变了允许的参数组合区域。模型仍然会选择产生最低损失的参数组合——最接近受约束区域中真正的最小化器 θ ^ No?Reg \hat{\theta}_{\text{No Reg}} θ^No?Reg?的点。
如果我们使
Q
Q
Q更小: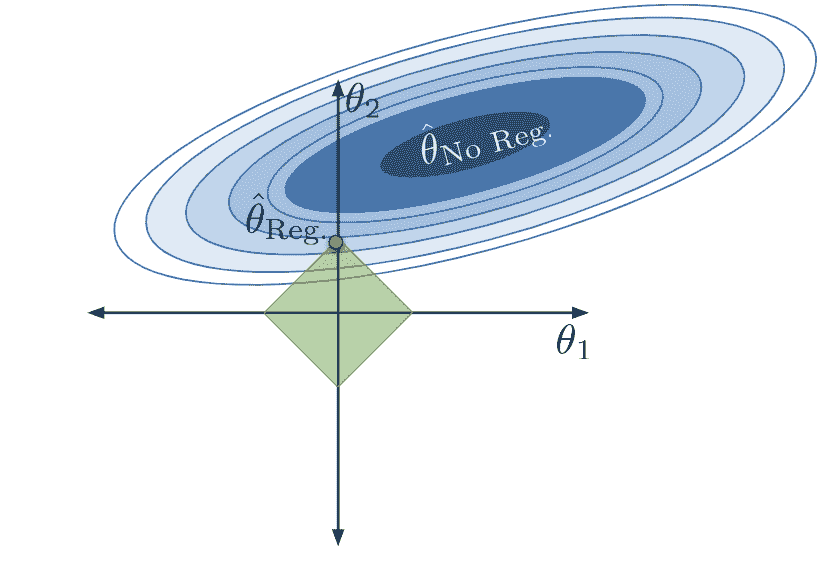 如果我们使
Q
Q
Q更大:
如果我们使
Q
Q
Q更大:
-
当 Q Q Q很小时,我们严重限制参数的大小。 θ i \theta_i θi?的值很小,特征 ? i \phi_i ?i?对模型的贡献很小。模型参数的允许区域收缩,模型变得简单得多。
-
当 Q Q Q很大时,我们并不严重限制参数的大小。 θ i \theta_i θi?的值很大,特征 ? i \phi_i ?i?对模型的贡献更大。模型参数的允许区域扩大,模型变得更复杂。
考虑当 Q Q Q极大时的极端情况。在这种情况下,我们的限制基本上没有效果,允许的区域包括 OLS 解!

现在如果 Q Q Q非常小会怎么样?我们的参数将被设置为(基本上是 0)。如果模型没有截距项: Y ^ = ( 0 ) ? 1 + ( 0 ) ? 2 + … = 0 \hat{\mathbb{Y}} = (0)\phi_1 + (0)\phi_2 + \ldots = 0 Y^=(0)?1?+(0)?2?+…=0。如果模型有一个截距项: Y ^ = ( 0 ) ? 1 + ( 0 ) ? 2 + … = θ 0 \hat{\mathbb{Y}} = (0)\phi_1 + (0)\phi_2 + \ldots = \theta_0 Y^=(0)?1?+(0)?2?+…=θ0?。请记住,截距项被排除在约束之外——这样我们就避免了总是预测 0 的情况。
让我们总结一下我们所看到的。
16.4 L1(LASSO)正则化
我们如何实际应用我们的约束 ∑ i = 1 p ∣ θ i ∣ ≤ Q \sum_{i=1}^p |\theta_i| \leq Q ∑i=1p?∣θi?∣≤Q?我们将通过修改我们在拟合模型时寻求最小化的目标函数来实现。
回想一下我们的普通最小二乘目标函数:我们的目标是找到最小化模型均方误差的参数。
1 n ∑ i = 1 n ( y i ? y ^ i ) 2 = 1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 ? i , 1 + θ 2 ? i , 2 + … + θ p ? i , p ) ) 2 \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 \phi_{i, 1} + \theta_2 \phi_{i, 2} + \ldots + \theta_p \phi_{i, p}))^2 n1?i=1∑n?(yi??y^?i?)2=n1?i=1∑n?(yi??(θ0?+θ1??i,1?+θ2??i,2?+…+θp??i,p?))2
要应用我们的约束,我们需要重新表述我们的最小化目标。
1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 ? i , 1 + θ 2 ? i , 2 + … + θ p ? i , p ) ) 2 ? such?that ∑ i = 1 p ∣ θ i ∣ ≤ Q \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 \phi_{i, 1} + \theta_2 \phi_{i, 2} + \ldots + \theta_p \phi_{i, p}))^2\:\text{such that} \sum_{i=1}^p |\theta_i| \leq Q n1?i=1∑n?(yi??(θ0?+θ1??i,1?+θ2??i,2?+…+θp??i,p?))2such?thati=1∑p?∣θi?∣≤Q
不幸的是,我们不能直接使用这个公式作为我们的目标函数——在约束上进行数学优化并不容易。相反,我们将应用拉格朗日对偶的魔力。这方面的细节超出了范围(如果你有兴趣了解更多,请参加 EECS 127 课程),但最终结果非常有用。事实证明,最小化以下增广目标函数等同于我们上面的最小化目标。
1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 ? i , 1 + θ 2 ? i , 2 + … + θ p ? i , p ) ) 2 + λ ∑ i = 1 p ∣ θ i ∣ = ∣ ∣ Y ? X θ ∣ ∣ 2 2 + λ ∑ i = 1 p ∣ θ i ∣ \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 \phi_{i, 1} + \theta_2 \phi_{i, 2} + \ldots + \theta_p \phi_{i, p}))^2 + \lambda \sum_{i=1}^p \vert \theta_i \vert = ||\mathbb{Y} - \mathbb{X}\theta||_2^2 + \lambda \sum_{i=1}^p |\theta_i| n1?i=1∑n?(yi??(θ0?+θ1??i,1?+θ2??i,2?+…+θp??i,p?))2+λi=1∑p?∣θi?∣=∣∣Y?Xθ∣∣22?+λi=1∑p?∣θi?∣
这两个表达式中的第二个包括使用向量表示的 MSE。
注意,我们已经用目标函数中的第二项替换了约束。我们现在正在最小化一个带有额外正则化项的函数,该项惩罚大的系数。为了最小化这个新的目标函数,我们最终会平衡两个组成部分:
-
保持模型在训练数据上的误差低,表示为术语 1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 x i , 1 + θ 2 x i , 2 + … + θ p x i , p ) ) 2 \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 x_{i, 1} + \theta_2 x_{i, 2} + \ldots + \theta_p x_{i, p}))^2 n1?∑i=1n?(yi??(θ0?+θ1?xi,1?+θ2?xi,2?+…+θp?xi,p?))2
-
同时,保持模型参数的幅度低,表示为术语 λ ∑ i = 1 p ∣ θ i ∣ \lambda \sum_{i=1}^p |\theta_i| λ∑i=1p?∣θi?∣
λ \lambda λ因子控制正则化的程度。粗略地说, λ \lambda λ与之前的 Q Q Q约束相关,规则为 λ ≈ 1 Q \lambda \approx \frac{1}{Q} λ≈Q1?。
为了理解原因,让我们考虑两个极端的例子:
-
假设 λ → ∞ \lambda \rightarrow \infty λ→∞。那么, λ ∑ j = 1 d ∣ θ j ∣ \lambda \sum_{j=1}^{d} \vert \theta_j \vert λ∑j=1d?∣θj?∣ 主导成本函数。为了最小化这个项,我们对所有 j ≥ 1 j \ge 1 j≥1设置 θ j = 0 \theta_j = 0 θj?=0。这是一个非常受限的模型,从数学上讲等同于常数模型。早些时候,我们解释了当 L2 范数球半径 Q → 0 Q \rightarrow 0 Q→0时,常数模型也会出现。
-
假设 λ → 0 \lambda \rightarrow 0 λ→0。那么, λ ∑ j = 1 d ∣ θ j ∣ \lambda \sum_{j=1}^{d} \vert \theta_j \vert λ∑j=1d?∣θj?∣为 0。最小化成本函数等价于 min ? θ 1 n ∣ ∣ Y ? X θ ∣ ∣ 2 2 \min_{\theta} \frac{1}{n} || Y - X\theta ||_2^2 minθ?n1?∣∣Y?Xθ∣∣22?,我们通常的 MSE 损失函数。最小化 MSE 损失的行为就是我们熟悉的 OLS,最优解是全局最小值 θ ^ = θ ^ N o R e g . \hat{\theta} = \hat\theta_{No Reg.} θ^=θ^NoReg.?。我们表明当 L2 范数球半径 Q → ∞ Q \rightarrow \infty Q→∞时,全局最优解被实现。
我们称 λ \lambda λ为正则化惩罚超参数,并通过交叉验证选择其值。
找到最优 θ ^ \hat{\theta} θ^以最小化我们的新目标函数的过程称为L1 正则化。它有时也被称为首字母缩写“LASSO”,代表“最小绝对收缩和选择算子”。
与普通最小二乘法不同,可以通过封闭形式解
θ
^
O
L
S
=
(
X
?
X
)
?
1
X
?
Y
\hat{\theta}_{OLS} = (\mathbb{X}^{\top}\mathbb{X})^{-1}\mathbb{X}^{\top}\mathbb{Y}
θ^OLS?=(X?X)?1X?Y来解决,L1 正则化下的最优参数向量没有封闭形式解。相反,我们使用sklearn的Lasso模型类。
import sklearn.linear_model as lm
# The alpha parameter represents our lambda term
lasso_model = lm.Lasso(alpha=2)
lasso_model.fit(X_train, Y_train)
lasso_model.coef_
array([-2.54932056e-01, -9.48597165e-04, 8.91976284e-06, -1.22872290e-08])
注意所有模型系数的幅度都非常小。实际上,其中一些系数非常小,基本上为 0。L1 正则化的一个重要特征是许多模型参数被设置为 0。换句话说,LASSO 有效地只选择了一部分特征。这一原因可以追溯到我们先前的损失曲面和允许的“菱形”区域 - 我们通常可以在菱形的一个角附近更接近最低损失轮廓,而不是沿着边缘。
当模型参数设置为 0 或接近 0 时,其对应的特征基本上从模型中移除了。我们说 L1 正则化执行特征选择,因为通过将不重要特征的参数设置为 0,LASSO“选择”了哪些特征对建模更有用。
16.5 特征缩放用于正则化
我们刚刚执行的正则化过程有一个微妙的问题。为了看清楚,让我们来看看我们的lasso_model的设计矩阵。
X_train.head()
| hp | hp^2 | hp^3 | hp^4 | |
|---|---|---|---|---|
| 259 | 85.0 | 7225.0 | 614125.0 | 52200625.0 |
| 129 | 67.0 | 4489.0 | 300763.0 | 20151121.0 |
| 207 | 102.0 | 10404.0 | 1061208.0 | 108243216.0 |
| 302 | 70.0 | 4900.0 | 343000.0 | 24010000.0 |
| 71 | 97.0 | 9409.0 | 912673.0 | 88529281.0 |
我们的特征——hp、hp^2、hp^3和hp^4——在数值尺度上有着截然不同的差异!hp^4中的值比hp中的值大几个数量级!这可能是一个问题,因为hp^4的值自然上会对每个预测的
y
^
\hat{y}
y^?贡献更多,因为它比其他特征的值大得多。对于hp对每个预测产生影响,它必须被一个大的模型参数所缩放。
通过检查我们模型的拟合参数,我们发现这种情况确实存在——hp的参数的数量级远大于hp^4的参数。
pd.DataFrame({"Feature":X_train.columns, "Parameter":lasso_model.coef_})
| Feature | Parameter | |
|---|---|---|
| 0 | hp | -2.549321e-01 |
| 1 | hp^2 | -9.485972e-04 |
| 2 | hp^3 | 8.919763e-06 |
| 3 | hp^4 | -1.228723e-08 |
通过应用正则化,我们给我们的模型一个“预算”,来分配模型参数的值。为了让hp对每个预测产生影响,LASSO 被迫在hp的参数上“花费”更多的预算。
我们可以通过在正则化之前对数据进行缩放来避免这个问题。这是一个过程,我们将所有特征转换为相同的数值尺度。一个常见的缩放数据的方法是进行标准化,使得所有特征的均值为 0,标准差为 1;基本上,我们用 Z 分数替换所有内容。
z k = x k ? μ k σ k z_k = \frac{x_k - \mu_k}{\sigma_k} zk?=σk?xk??μk??
16.6 L2(岭)正则化
在我们上面的所有工作中,我们考虑了约束 ∑ i = 1 p ∣ θ i ∣ ≤ Q \sum_{i=1}^p |\theta_i| \leq Q ∑i=1p?∣θi?∣≤Q来限制模型的复杂性。如果我们应用了不同的约束会怎样呢?
在 L2 正则化中,也被称为岭回归,我们约束模型,使得平方参数的总和必须小于某个数 Q Q Q。这个约束的形式如下:
∑ i = 1 p θ i 2 ≤ Q \sum_{i=1}^p \theta_i^2 \leq Q i=1∑p?θi2?≤Q
与以前一样,我们通常不对截距项进行正则化。
对于给定的 Q Q Q值,参数的允许区域现在呈球状。
如果我们像之前一样修改我们的目标函数,我们发现我们的新目标是最小化函数: 1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 ? i , 1 + θ 2 ? i , 2 + … + θ p ? i , p ) ) 2 ? such?that ∑ i = 1 p θ i 2 ≤ Q \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 \phi_{i, 1} + \theta_2 \phi_{i, 2} + \ldots + \theta_p \phi_{i, p}))^2\:\text{such that} \sum_{i=1}^p \theta_i^2 \leq Q n1?i=1∑n?(yi??(θ0?+θ1??i,1?+θ2??i,2?+…+θp??i,p?))2such?thati=1∑p?θi2?≤Q
请注意,我们所做的只是改变了模型参数的约束。表达式中的第一项,均方误差,没有改变。
使用拉格朗日对偶性,我们可以重新表达我们的目标函数为: 1 n ∑ i = 1 n ( y i ? ( θ 0 + θ 1 ? i , 1 + θ 2 ? i , 2 + … + θ p ? i , p ) ) 2 + λ ∑ i = 1 p θ i 2 = ∣ ∣ Y ? X θ ∣ ∣ 2 2 + λ ∑ i = 1 p θ i 2 \frac{1}{n} \sum_{i=1}^n (y_i - (\theta_0 + \theta_1 \phi_{i, 1} + \theta_2 \phi_{i, 2} + \ldots + \theta_p \phi_{i, p}))^2 + \lambda \sum_{i=1}^p \theta_i^2 = ||\mathbb{Y} - \mathbb{X}\theta||_2^2 + \lambda \sum_{i=1}^p \theta_i^2 n1?i=1∑n?(yi??(θ0?+θ1??i,1?+θ2??i,2?+…+θp??i,p?))2+λi=1∑p?θi2?=∣∣Y?Xθ∣∣22?+λi=1∑p?θi2?
应用 L2 正则化时,我们的目标是最小化这个更新的目标函数。
与 L1 正则化不同,L2 正则化在应用正则化时确实有一个最佳参数向量的封闭形式解:
θ ^ ridge = ( X ? X + n λ I ) ? 1 X ? Y \hat\theta_{\text{ridge}} = (\mathbb{X}^{\top}\mathbb{X} + n\lambda I)^{-1}\mathbb{X}^{\top}\mathbb{Y} θ^ridge?=(X?X+nλI)?1X?Y
即使 X \mathbb{X} X不是完全列秩,这个解仍然存在。这是 L2 正则化经常被使用的一个主要原因——即使特征中存在共线性,它也可以产生一个解。我们将在未来的讲座中讨论共线性的概念。我们不会在 Data 100 中推导这个结果,因为它涉及相当多的矩阵微积分。
在sklearn中,我们使用Ridge类来执行 L2 正则化。请注意,在正则化之前我们会对数据进行缩放。
ridge_model = lm.Ridge(alpha=1) # alpha represents the hyperparameter lambda
ridge_model.fit(X_train, Y_train)
ridge_model.coef_
array([ 5.89130559e-02, -6.42445915e-03, 4.44468157e-05, -8.83981945e-08])
16.7 回归总结
我们的回归模型总结如下。请注意,目标函数是梯度下降优化器最小化的内容。
| 类型 | 模型 | 损失 | 正则化 | 目标函数 | 解决方案 |
|---|---|---|---|---|---|
| 普通最小二乘法(OLS) | Y ^ = X θ \hat{\mathbb{Y}} = \mathbb{X}\theta Y^=Xθ | 均方误差 | 无 | 1 n ∣ Y ? X θ ∣ 2 2 \frac{1}{n} |\mathbb{Y}-\mathbb{X} \theta|^2_2 n1?∣Y?Xθ∣22? | θ ^ O L S = ( X ? X ) ? 1 X ? Y \hat{\theta}_{OLS} = (\mathbb{X}^{\top}\mathbb{X})^{-1}\mathbb{X}^{\top}\mathbb{Y} θ^OLS?=(X?X)?1X?Y 如果 X \mathbb{X} X 是满秩的 |
| 岭回归 | Y ^ = X θ \hat{\mathbb{Y}} = \mathbb{X} \theta Y^=Xθ | 均方误差 | L2 | 1 n ∥ Y ? X θ ∥ 2 2 + λ ∑ i = 1 p θ i 2 \frac{1}{n} \|\mathbb{Y}-\mathbb{X}\theta\|^2_2 + \lambda \sum_{i=1}^p \theta_i^2 n1?∥Y?Xθ∥22?+λ∑i=1p?θi2? | θ ^ r i d g e = ( X ? X + n λ I ) ? 1 X ? Y \hat{\theta}_{ridge} = (\mathbb{X}^{\top}\mathbb{X} + n \lambda I)^{-1}\mathbb{X}^{\top}\mathbb{Y} θ^ridge?=(X?X+nλI)?1X?Y |
| LASSO | Y ^ = X θ \hat{\mathbb{Y}} = \mathbb{X} \theta Y^=Xθ | 均方误差 | L1 | 1 n ∥ Y ? X θ ∥ 2 2 + λ ∑ i = 1 p ∣ θ i ∣ \frac{1}{n} \|\mathbb{Y}-\mathbb{X}\theta\|^2_2 + \lambda \sum_{i=1}^p \vert \theta_i \vert n1?∥Y?Xθ∥22?+λ∑i=1p?∣θi?∣ | 无闭式解 |
十七、随机变量
译者:飞龙
学习成果
-
以其分布的形式定义随机变量
-
计算随机变量的期望和方差
-
熟悉伯努利和二项式随机变量
在过去的几节课中,我们已经考虑了复杂性对模型性能的影响。我们已经考虑了模型复杂性在两个竞争因素之间的权衡:模型方差和训练误差。
到目前为止,我们的分析大部分是定性的。我们已经承认我们对模型复杂性的选择需要在模型方差和训练误差之间取得平衡,但我们还没有讨论为什么会存在这种权衡。
为了更好地理解这种权衡的起源,我们需要引入随机变量的语言。接下来的两节关于概率的讲座将是对我们在建模工作中的一个简短的离题,这样我们就可以建立起理解这所谓的偏差-方差权衡所需的概念。我们接下来几节的路线图将是:
-
随机变量估计器:引入随机变量,考虑期望、方差和协方差的概念
-
估计器、偏差和方差:用随机变量的术语重新表达模型方差和训练误差的概念,并利用这种新的视角来研究我们对模型复杂性的选择
Data 8 复习
-
回顾 Data 8 中的以下概念:
-
样本均值:你的随机样本的均值
-
中心极限定理:如果你进行了一个带有替换的大样本随机抽样,那么无论总体分布如何,样本均值的概率分布
-
大致是正态的
-
以总体均值为中心
-
有一个 S D = 总体?SD 样本大小 SD = \frac{\text{总体 SD}}{\sqrt{\text{样本大小}}} SD=样本大小?总体?SD?
-
17.1 随机变量和分布
假设我们生成了一组随机数据,比如从某个总体中随机抽取的一个随机样本。随机变量是数据中随机性的数值函数。它是随机的,因为我们的样本是随机抽取的;它是变量的,因为它的确切值取决于这个随机样本的结果。因此,我们的随机变量的定义域或输入是一个样本空间中所有可能的(随机的)结果,它的值域或输出是数轴。我们通常用大写字母表示随机变量,如 X X X或 Y Y Y。
17.1.1 分布
对于任何随机变量 X X X,我们需要能够指定两件事:
-
可能的值:随机变量可以取得的值的集合。
-
概率:描述 100%总概率如何分布在可能值上的概率集合。
如果 X X X是离散的(有有限个可能的值),随机变量 X X X取值 x x x的概率由 P ( X = x ) P(X=x) P(X=x)给出,概率必须总和为 1: ∑ all x P ( X = x ) = 1 \sum_{\text{all} x} P(X=x) = 1 ∑allx?P(X=x)=1,
我们通常可以使用概率分布表来显示这一点,你将在下面的抛硬币示例中看到。
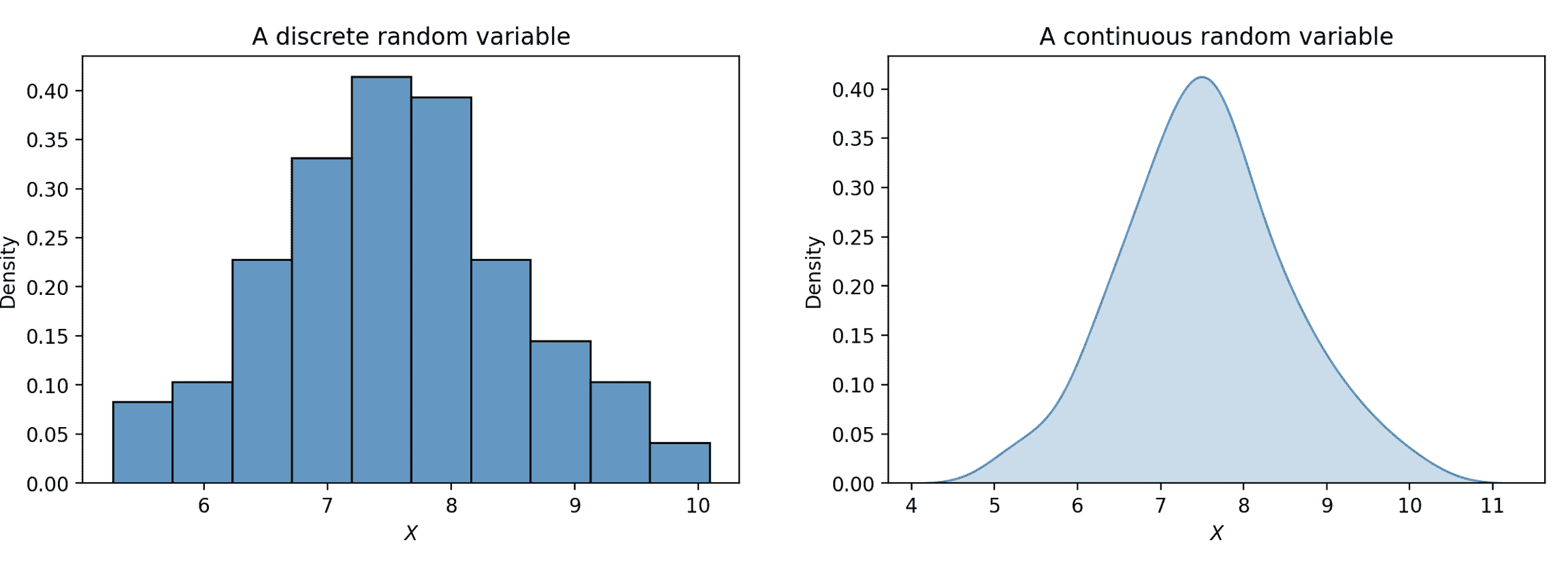
随机变量 X X X的分布是对 100%总概率如何分布在 X X X的所有可能值上的描述,它完全定义了一个随机变量。离散随机变量的分布也可以用直方图表示。如果一个变量是连续的 - 它可以取无限多个值 - 我们可以用密度曲线来说明它的分布。
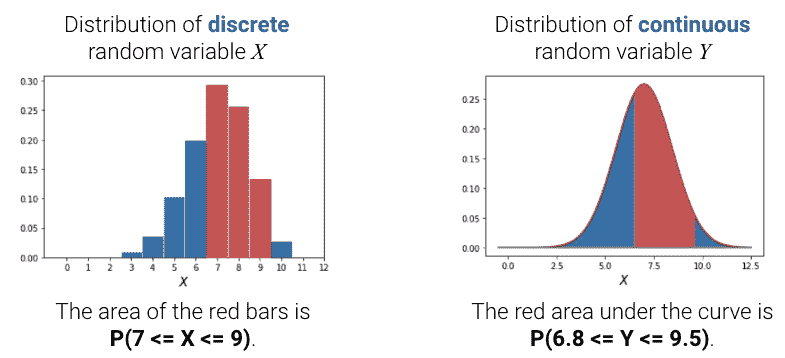
概率是区域。对于离散随机变量,红色条形的面积表示离散随机变量 X X X落在这些值范围内的概率。对于连续随机变量,曲线下的面积表示离散随机变量 Y Y Y落在这些值范围内的概率。
如果我们将条形图/密度曲线下的总面积相加,应该得到 100%,或 1。
17.1.2 例子:抛硬币
举个具体的例子,让我们正式定义一个公平的硬币抛掷。一枚公平的硬币可以正面朝上( H H H)或反面朝上( T T T),每种情况的概率都是 0.5。有了这些可能的结果,我们可以将随机变量 X X X定义为: X = { 1 , 如果硬币正面朝上 0 , 如果硬币反面朝上 X = \begin{cases} 1, \text{如果硬币正面朝上} \\ 0, \text{如果硬币反面朝上} \end{cases} X={1,如果硬币正面朝上0,如果硬币反面朝上?
X X X是一个具有域或输入 { H , T } \{H, T\} {H,T}和值域或输出 { 1 , 0 } \{1, 0\} {1,0}的函数。我们可以用函数符号表示为 { X ( H ) = 1 X ( T ) = 0 \begin{cases} X(H) = 1 \\ X(T) = 0 \end{cases} {X(H)=1X(T)=0? X X X的概率分布表如下。
| x x x | P ( X = x ) P(X=x) P(X=x) |
|---|---|
| 0 | 1 2 \frac{1}{2} 21? |
| 1 | 1 2 \frac{1}{2} 21? |
假设我们从 Data 100 中所有注册学生中随机抽取一个大小为 3 的样本 s s s。我们可以将 Y Y Y定义为我们样本中数据科学学生的数量。它的域是大小为 3 的所有可能样本,其值域是 { 0 , 1 , 2 , 3 } \{0, 1, 2, 3\} {0,1,2,3}。
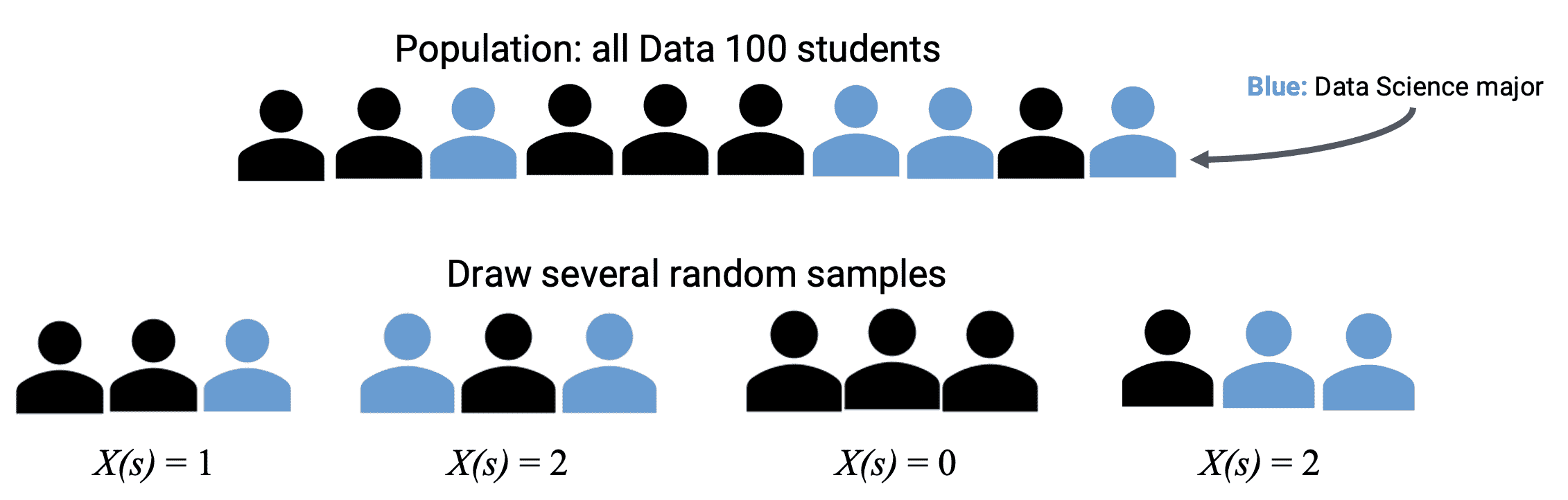
我们可以在下表中显示 Y Y Y的分布。左侧的表列出了所有可能的样本 s s s及其出现次数( Y ( s ) Y(s) Y(s))。我们可以使用这个来计算右侧的表的值,即概率分布表。

17.1.3 模拟
给定随机变量
X
X
X的分布,我们如何生成/模拟一个总体?为此,我们可以根据其分布随机选择
X
X
X的值,使用np.random.choice或df.sample。
17.2 期望和方差
描述随机变量的方法有几种。上面显示的方法 - 所有样本 s , X ( s ) s, X(s) s,X(s)的表,分布表 P ( X = x ) P(X=x) P(X=x)和直方图 - 都是完全描述随机变量的定义。通常,用一些数值摘要来描述随机变量比完全定义其分布更容易。这些数值摘要是表征随机变量某些属性的数字。因为它们给出了随机变量的行为倾向的“摘要”,它们不是随机的 - 将它们视为描述随机变量某个属性的静态数字。在 Data 100 中,我们将关注随机变量的期望和方差。
17.2.1 期望
随机变量 X X X的期望是 X X X的值的加权平均值,其中权重是每个值发生的概率。有两种等效的计算期望的方法:
-
一次应用一个样本的权重: E [ X ] = ∑ 所有可能的 s X ( s ) P ( s ) \mathbb{E}[X] = \sum_{\text{所有可能的} s} X(s) P(s) E[X]=所有可能的s∑?X(s)P(s)。
-
一次应用权重一个可能的值: E [ X ] = ∑ 所有可能的 x x P ( X = x ) \mathbb{E}[X] = \sum_{\text{所有可能的} x} x P(X=x) E[X]=所有可能的x∑?xP(X=x)
我们要强调的是,期望是一个数字,不是一个随机变量。期望是平均值的一种概括,它与随机变量具有相同的单位。它也是概率分布直方图的重心,这意味着如果我们多次模拟变量,它是随机变量的长期平均值。
17.2.1.1 示例 1:抛硬币
回到我们抛硬币的例子,我们将随机变量 X X X定义为: X = { 1 , 如果硬币正面朝上 0 , 如果硬币反面朝上 X = \begin{cases} 1, \text{如果硬币正面朝上} \\ 0, \text{如果硬币反面朝上} \end{cases} X={1,如果硬币正面朝上0,如果硬币反面朝上? 我们可以使用第二种方法,一次应用权重一个可能的值来计算其期望 E [ X ] \mathbb{E}[X] E[X]: E [ X ] = ∑ x x P ( X = x ) = 1 ? 0.5 + 0 ? 0.5 = 0.5 \begin{align} \mathbb{E}[X] &= \sum_{x} x P(X=x) \\ &= 1 * 0.5 + 0 * 0.5 \\ &= 0.5 \end{align} E[X]?=x∑?xP(X=x)=1?0.5+0?0.5=0.5?? 请注意, E [ X ] = 0.5 \mathbb{E}[X] = 0.5 E[X]=0.5不是 X X X的可能值;这是一个平均值。X 的期望值不需要是 X 的可能值。
17.2.1.2 示例 2
考虑随机变量 X X X:
| x x x | P ( X = x ) P(X=x) P(X=x) |
|---|---|
| 3 | 0.1 |
| 4 | 0.2 |
| 6 | 0.4 |
| 8 | 0.3 |
计算期望, E [ X ] = ∑ x x P ( X = x ) = 3 ? 0.1 + 4 ? 0.2 + 6 ? 0.4 + 8 ? 0.3 = 0.3 + 0.8 + 2.4 + 2.4 = 5.9 \begin{align} \mathbb{E}[X] &= \sum_{x} x P(X=x) \\ &= 3 * 0.1 + 4 * 0.2 + 6 * 0.4 + 8 * 0.3 \\ &= 0.3 + 0.8 + 2.4 + 2.4 \\ &= 5.9 \end{align} E[X]?=x∑?xP(X=x)=3?0.1+4?0.2+6?0.4+8?0.3=0.3+0.8+2.4+2.4=5.9?? 再次注意, E [ X ] = 5.9 \mathbb{E}[X] = 5.9 E[X]=5.9 不是 X X X 的可能值;这是一个平均值。X 的期望值不需要是 X 的可能值。
17.2.2 方差
随机变量的方差是其随机误差的度量。它被定义为 X X X的期望值的平方偏差。更简单地说,方差问: X X X通常从其平均值变化多少,仅仅是由于偶然? X X X的分布是如何传播的?
Var ( X ) = E [ ( X ? E [ X ] ) 2 ] \text{Var}(X) = \mathbb{E}[(X-\mathbb{E}[X])^2] Var(X)=E[(X?E[X])2]
方差的单位是 X X X的单位的平方。要将其恢复到正确的比例,使用 X X X的标准差: SD ( X ) = Var ( X ) \text{SD}(X) = \sqrt{\text{Var}(X)} SD(X)=Var(X)?
与期望一样,方差是一个数,不是一个随机变量!它的主要用途是量化偶然误差。
根据切比雪夫不等式,你在 Data 8 中看到的,无论 X X X的分布形状如何,绝大多数的概率都在“期望值加上或减去几个标准差”的区间内。
如果我们展开平方并使用期望的属性,我们可以重新表达方差作为方差的计算公式。当手动计算变量的方差时,这种形式通常更方便使用,并且在均方误差计算中也很有用,因为如果 X X X是居中的,那么 E [ X 2 ] = Var ( X ) \mathbb{E}[X^2] = \text{Var}(X) E[X2]=Var(X)。
Var ( X ) = E [ X 2 ] ? ( E [ X ] ) 2 \text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 Var(X)=E[X2]?(E[X])2
证明
Var ( X ) = E [ ( X ? E [ X ] ) 2 ] = E ( X 2 ? 2 X E ( X ) + ( E ( X ) ) 2 ) = E ( X 2 ) ? 2 E ( X ) E ( X ) + ( E ( X ) ) 2 = E [ X 2 ] ? ( E [ X ] ) 2 \begin{align} \text{Var}(X) &= \mathbb{E}[(X-\mathbb{E}[X])^2] \\ &= \mathbb{E}(X^2 - 2X\mathbb{E}(X) + (\mathbb{E}(X))^2) \\ &= \mathbb{E}(X^2) - 2 \mathbb{E}(X)\mathbb{E}(X) +( \mathbb{E}(X))^2\\ &= \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \end{align} Var(X)?=E[(X?E[X])2]=E(X2?2XE(X)+(E(X))2)=E(X2)?2E(X)E(X)+(E(X))2=E[X2]?(E[X])2??
我们如何计算 E [ X 2 ] \mathbb{E}[X^2] E[X2]? 任何随机变量的函数也是随机变量 - 这意味着通过平方 X X X,我们创建了一个新的随机变量。要计算 E [ X 2 ] \mathbb{E}[X^2] E[X2],我们可以简单地将我们的期望值定义应用于随机变量 X 2 X^2 X2。
E [ X 2 ] = ∑ x x 2 P ( X = x ) \mathbb{E}[X^2] = \sum_{x} x^2 P(X = x) E[X2]=x∑?x2P(X=x)
17.2.3 例子:骰子
设 X X X是单次公平掷骰子的结果。 X X X是一个随机变量,定义为 X = { 1 6 , if? x ∈ { 1 , 2 , 3 , 4 , 5 , 6 } 0 , otherwise X = \begin{cases} \frac{1}{6}, \text{if } x \in \{1,2,3,4,5,6\} \\ 0, \text{otherwise} \end{cases} X={61?,if?x∈{1,2,3,4,5,6}0,otherwise?
期望值 E [ X ] ? \mathbb{E}[X]? E[X]?
E [ X ] = 1 ( 1 6 ) + 2 ( 1 6 ) + 3 ( 1 6 ) + 4 ( 1 6 ) + 5 ( 1 6 ) + 6 ( 1 6 ) = ( 1 6 ) ( 1 + 2 + 3 + 4 + 5 + 6 ) = 7 2 \begin{align} \mathbb{E}[X] &= 1(\frac{1}{6}) + 2(\frac{1}{6}) + 3(\frac{1}{6}) + 4(\frac{1}{6}) + 5(\frac{1}{6}) + 6(\frac{1}{6}) \\ &= (\frac{1}{6}) ( 1 + 2 + 3 + 4 + 5 + 6) \\ &= \frac{7}{2} \end{align} E[X]?=1(61?)+2(61?)+3(61?)+4(61?)+5(61?)+6(61?)=(61?)(1+2+3+4+5+6)=27???
方差 Var ( X ) ? \text{Var}(X)? Var(X)?
使用方法 1: Var ( X ) = ( 1 6 ) ( ( 1 ? 7 2 ) 2 + ( 2 ? 7 2 ) 2 + ( 3 ? 7 2 ) 2 + ( 4 ? 7 2 ) 2 + ( 5 ? 7 2 ) 2 + ( 6 ? 7 2 ) 2 ) = 35 12 \begin{align} \text{Var}(X) &= (\frac{1}{6})((1 - \frac{7}{2})^2 + (2 - \frac{7}{2})^2 + (3 - \frac{7}{2})^2 + (4 - \frac{7}{2})^2 + (5 - \frac{7}{2})^2 + (6 - \frac{7}{2})^2) \\ &= \frac{35}{12} \end{align} Var(X)?=(61?)((1?27?)2+(2?27?)2+(3?27?)2+(4?27?)2+(5?27?)2+(6?27?)2)=1235???
使用方法 2: E [ X 2 ] = ∑ x x 2 P ( X = x ) = 91 6 \mathbb{E}[X^2] = \sum_{x} x^2 P(X = x) = \frac{91}{6} E[X2]=x∑?x2P(X=x)=691?
Var ( X ) = 91 6 ? ( 7 2 ) 2 = 35 12 \text{Var}(X) = \frac{91}{6} - (\frac{7}{2})^2 = \frac{35}{12} Var(X)=691??(27?)2=1235?
17.3 随机变量的和
通常,我们会同时处理多个随机变量。随机变量的函数也是随机变量;如果你基于样本创建多个随机变量,那么这些随机变量的函数也是随机变量。
例如,如果 X 1 , X 2 , . . . , X n X_1, X_2, ..., X_n X1?,X2?,...,Xn?是随机变量,那么这些也是随机变量:
-
X n 2 X_n^2 Xn2?
-
# { i : X i > 10 } \#\{i : X_i > 10\} #{i:Xi?>10}
-
max ( X 1 , X 2 , . . . , X n ) \text{max}(X_1, X_2, ..., X_n) max(X1?,X2?,...,Xn?)
-
1 n ∑ i = 1 n ( X i ? c ) 2 \frac{1}{n} \sum_{i=1}^n (X_i - c)^2 n1?∑i=1n?(Xi??c)2
-
1 n ∑ i = 1 n X i \frac{1}{n} \sum_{i=1}^n X_i n1?∑i=1n?Xi?
17.3.1 相等 vs. 相同分布 vs. i.i.d.
假设我们有两个随机变量 X X X 和 Y Y Y:
-
X X X 和 Y Y Y 如果对于每个样本 s s s 都有 X ( s ) = Y ( s ) X(s) = Y(s) X(s)=Y(s) 则它们是相等的。无论抽取的确切样本是什么, X X X 总是等于 Y Y Y。
-
如果 X X X和 Y Y Y的分布相等,则 X X X和 Y Y Y是相同分布的。我们说“X 和 Y 在分布上相等”。也就是说, X X X和 Y Y Y取相同的可能值集,并且每个可能值都以相同的概率取到。在任何特定的样本 s s s上,相同分布的变量不一定共享相同的值。如果 X = Y,则 X 和 Y 是相同分布的;然而,反之则不成立(例如:Y = 7-X,X 是一个骰子)
-
如果
-
这些变量是相同分布的。
-
知道一个变量的结果不会影响我们对另一个变量结果的信念。
-
例如,让 X 1 X_1 X1?和 X 2 X_2 X2?是两个公平骰子的点数。 X 1 X_1 X1?和 X 2 X_2 X2?是 i.i.d,所以 X 1 X_1 X1?和 X 2 X_2 X2?具有相同的分布。然而,和 Y = X 1 + X 1 = 2 X 1 Y = X_1 + X_1 = 2X_1 Y=X1?+X1?=2X1?和 Z = X 1 + X 2 Z=X_1+X_2 Z=X1?+X2?具有不同的分布,但是相同的期望值。
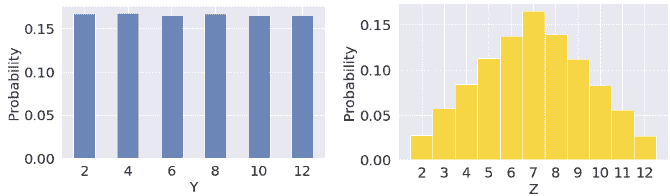
然而, Y = X 1 Y = X_1 Y=X1?的方差更大

17.3.2 期望值的性质
我们经常直接计算期望值和方差,而不是模拟完整的分布。回顾期望值的定义: E [ X ] = ∑ x x P ( X = x ) \mathbb{E}[X] = \sum_{x} x P(X=x) E[X]=x∑?xP(X=x) 从中,我们可以推导出期望值的一些有用的性质:
- 期望的线性性。常数 a a a和 b b b的线性变换 a X + b aX+b aX+b的期望值是:
E [ a X + b ] = a E [ X ] + b \mathbb{E}[aX+b] = aE[\mathbb{X}] + b E[aX+b]=aE[X]+b
证明
E [ a X + b ] = ∑ x ( a x + b ) P ( X = x ) = ∑ x ( a x P ( X = x ) + b P ( X = x ) ) = a ∑ x P ( X = x ) + b ∑ x P ( X = x ) = a E ( X ) + b ? 1 \begin{align} \mathbb{E}[aX+b] &= \sum_{x} (ax + b) P(X=x) \\ &= \sum_{x} (ax P(X=x) + bP(X=x)) \\ &= a\sum_{x}P(X=x) + b\sum_{x}P(X=x)\\ &= a\mathbb{E}(X) + b * 1 \end{align} E[aX+b]?=x∑?(ax+b)P(X=x)=x∑?(axP(X=x)+bP(X=x))=ax∑?P(X=x)+bx∑?P(X=x)=aE(X)+b?1??
- 期望值在随机变量的总和中也是线性的。
E [ X + Y ] = E [ X ] + E [ Y ] \mathbb{E}[X+Y] = \mathbb{E}[X] + \mathbb{E}[Y] E[X+Y]=E[X]+E[Y]
证明
E [ X + Y ] = ∑ s ( X + Y ) ( s ) P ( s ) = ∑ s ( X ( s ) P ( s ) + Y ( s ) P ( s ) ) = ∑ s X ( s ) P ( s ) + ∑ s Y ( s ) P ( s ) = E [ X ] + E [ Y ] \begin{align} \mathbb{E}[X+Y] &= \sum_{s} (X+Y)(s) P(s) \\ &= \sum_{s} (X(s)P(s) + Y(s)P(s)) \\ &= \sum_{s} X(s)P(s) + \sum_{s} Y(s)P(s)\\ &= \mathbb{E}[X] + \mathbb{E}[Y] \end{align} E[X+Y]?=s∑?(X+Y)(s)P(s)=s∑?(X(s)P(s)+Y(s)P(s))=s∑?X(s)P(s)+s∑?Y(s)P(s)=E[X]+E[Y]??
- 如果 g g g是一个非线性函数,那么一般来说, E [ g ( X ) ] ≠ g ( E [ X ] ) \mathbb{E}[g(X)] \neq g(\mathbb{E}[X]) E[g(X)]=g(E[X]) 例如,如果 X X X以相等的概率为-1 或 1,那么 E [ X ] = 0 \mathbb{E}[X] = 0 E[X]=0,但 E [ X 2 ] = 1 ≠ 0 \mathbb{E}[X^2] = 1 \neq 0 E[X2]=1=0.
17.3.3 方差的性质
回顾方差的定义: Var ( X ) = E [ ( X ? E [ X ] ) 2 ] \text{Var}(X) = \mathbb{E}[(X-\mathbb{E}[X])^2] Var(X)=E[(X?E[X])2] 结合期望值的性质,我们可以推导出方差的一些有用的性质:
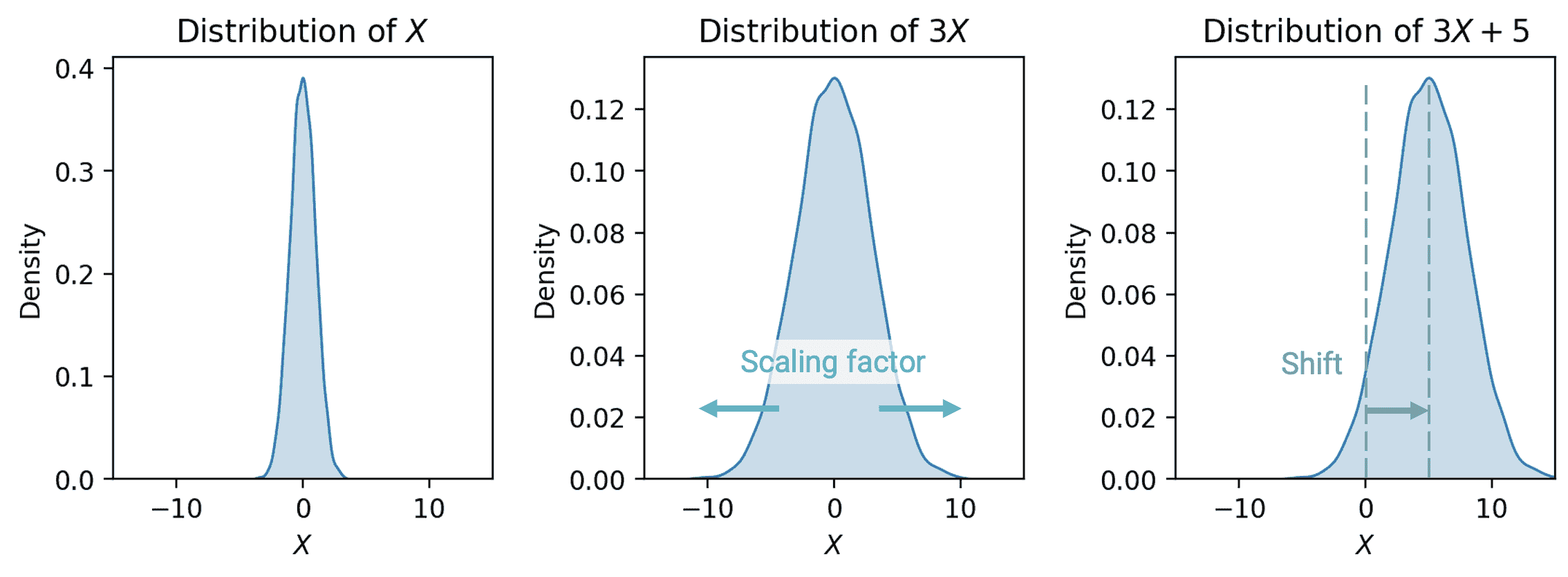
- 与期望值不同,方差是非线性的。线性变换 a X + b aX+b aX+b的方差是: Var ( a X + b ) = a 2 Var ( X ) \text{Var}(aX+b) = a^2 \text{Var}(X) Var(aX+b)=a2Var(X)
-
随后, SD ( a X + b ) = ∣ a ∣ SD ( X ) \text{SD}(aX+b) = |a| \text{SD}(X) SD(aX+b)=∣a∣SD(X)
-
可以通过方差的定义找到这个事实的完整证明。作为一般直觉,考虑 a X + b aX+b aX+b通过因子 a a a缩放变量 X X X,然后将 X X X的分布移位 b b b单位。
证明
我们知道 E [ a X + b ] = a E [ X ] + b \mathbb{E}[aX+b] = aE[\mathbb{X}] + b E[aX+b]=aE[X]+b
为了计算 Var ( a X + b ) \text{Var}(aX+b) Var(aX+b),考虑到 b 单位的移位不会影响扩展,因此 Var ( a X + b ) = Var ( a X ) \text{Var}(aX+b) = \text{Var}(aX) Var(aX+b)=Var(aX)。
因此, Var ( a X + b ) = Var ( a X ) = E ( ( a X ) 2 ) ? ( E ( a X ) ) 2 = E ( a 2 X 2 ) ? ( a E ( X ) ) 2 = a 2 ( E ( X 2 ) ? ( E ( X ) ) 2 ) = a 2 Var ( X ) \begin{align} \text{Var}(aX+b) &= \text{Var}(aX) \\ &= E((aX)^2) - (E(aX))^2 \\ &= E(a^2 X^2) - (aE(X))^2\\ &= a^2 (E(X^2) - (E(X))^2) \\ &= a^2 \text{Var}(X) \end{align} Var(aX+b)?=Var(aX)=E((aX)2)?(E(aX))2=E(a2X2)?(aE(X))2=a2(E(X2)?(E(X))2)=a2Var(X)??
- 将分布移位 b 不会 影响分布的扩展。因此, Var ( a X + b ) = Var ( a X ) \text{Var}(aX+b) = \text{Var}(aX) Var(aX+b)=Var(aX)。
- 通过 a a a缩放分布会 影响分布的扩展。
- 随机变量的和的方差受到随机变量的(不)独立性的影响。 Var ( X + Y ) = Var ( X ) + Var ( Y ) + 2 cov ( X , Y ) \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) + 2\text{cov}(X,Y) Var(X+Y)=Var(X)+Var(Y)+2cov(X,Y)
Var ( X + Y ) = Var ( X ) + Var ( Y ) if? X , Y ?independent \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) \qquad \text{if } X, Y \text{ independent} Var(X+Y)=Var(X)+Var(Y)if?X,Y?independent
证明
两个随机变量相加的方差受到它们之间的依赖关系的影响。让我们展开 Var ( X + Y ) \text{Var}(X + Y) Var(X+Y)的定义,看看发生了什么。
为了简化数学,让 μ x = E [ X ] \mu_x = \mathbb{E}[X] μx?=E[X]和 μ y = E [ Y ] \mu_y = \mathbb{E}[Y] μy?=E[Y]。
Var ( X + Y ) = E [ ( X + Y ? E ( X + Y ) ) 2 ] = E [ ( ( X ? μ x ) + ( Y ? μ y ) ) 2 ] = E [ ( X ? μ x ) 2 + 2 ( X ? μ x ) ( Y ? μ y ) + ( Y ? μ y ) 2 ] = E [ ( X ? μ x ) 2 ] + E [ ( Y ? μ y ) 2 ] + E [ ( X ? μ x ) ( Y ? μ y ) ] = Var ( X ) + Var ( Y ) + E [ ( X ? μ x ) ( Y ? μ y ) ] \begin{align} \text{Var}(X + Y) &= \mathbb{E}[(X+Y- \mathbb{E}(X+Y))^2] \\ &= \mathbb{E}[((X - \mu_x) + (Y - \mu_y))^2] \\ &= \mathbb{E}[(X - \mu_x)^2 + 2(X - \mu_x)(Y - \mu_y) + (Y - \mu_y)^2] \\ &= \mathbb{E}[(X - \mu_x)^2] + \mathbb{E}[(Y - \mu_y)^2] + \mathbb{E}[(X - \mu_x)(Y - \mu_y)] \\ &= \text{Var}(X) + \text{Var}(Y) + \mathbb{E}[(X - \mu_x)(Y - \mu_y)] \end{align} Var(X+Y)?=E[(X+Y?E(X+Y))2]=E[((X?μx?)+(Y?μy?))2]=E[(X?μx?)2+2(X?μx?)(Y?μy?)+(Y?μy?)2]=E[(X?μx?)2]+E[(Y?μy?)2]+E[(X?μx?)(Y?μy?)]=Var(X)+Var(Y)+E[(X?μx?)(Y?μy?)]??
17.3.4 Covariance and Correlation
我们将两个随机变量的协方差定义为期望的偏差乘积。更简单地说,协方差是方差对两个随机变量的泛化: Cov ( X , X ) = E [ ( X ? E [ X ] ) 2 ] = Var ( X ) \text{Cov}(X, X) = \mathbb{E}[(X - \mathbb{E}[X])^2] = \text{Var}(X) Cov(X,X)=E[(X?E[X])2]=Var(X)
Cov ( X , Y ) = E [ ( X ? E [ X ] ) ( Y ? E [ Y ] ) ] \text{Cov}(X, Y) = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] Cov(X,Y)=E[(X?E[X])(Y?E[Y])]
我们可以将协方差视为一种关联度量。还记得我们在建立简单线性回归时给出的相关性定义吗?
r ( X , Y ) = E [ ( X ? E [ X ] SD ( X ) ) ( Y ? E [ Y ] SD ( Y ) ) ] = Cov ( X , Y ) SD ( X ) SD ( Y ) r(X, Y) = \mathbb{E}\left[\left(\frac{X-\mathbb{E}[X]}{\text{SD}(X)}\right)\left(\frac{Y-\mathbb{E}[Y]}{\text{SD}(Y)}\right)\right] = \frac{\text{Cov}(X, Y)}{\text{SD}(X)\text{SD}(Y)} r(X,Y)=E[(SD(X)X?E[X]?)(SD(Y)Y?E[Y]?)]=SD(X)SD(Y)Cov(X,Y)?
事实证明我们一直在悄悄使用协方差!如果 X X X和 Y Y Y是独立的,那么 Cov ( X , Y ) = 0 \text{Cov}(X, Y) =0 Cov(X,Y)=0和 r ( X , Y ) = 0 r(X, Y) = 0 r(X,Y)=0。然而,请注意,逆命题并不总是成立: X X X和 Y Y Y可能有 Cov ( X , Y ) = r ( X , Y ) = 0 \text{Cov}(X, Y) = r(X, Y) = 0 Cov(X,Y)=r(X,Y)=0但并不是独立的。
17.3.5 Summary
-
设 X X X是一个具有分布 P ( X = x ) P(X=x) P(X=x)的随机变量。
-
E [ X ] = ∑ x x P ( X = x ) \mathbb{E}[X] = \sum_{x} x P(X=x) E[X]=∑x?xP(X=x)
-
Var ( X ) = E [ ( X ? E [ X ] ) 2 ] = E [ X 2 ] ? ( E [ X ] ) 2 \text{Var}(X) = \mathbb{E}[(X-\mathbb{E}[X])^2] = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 Var(X)=E[(X?E[X])2]=E[X2]?(E[X])2
-
-
设 a a a和 b b b是标量值。
-
E [ a X + b ] = a E [ X ] + b \mathbb{E}[aX+b] = aE[\mathbb{X}] + b E[aX+b]=aE[X]+b
-
Var ( a X + b ) = a 2 Var ( X ) \text{Var}(aX+b) = a^2 \text{Var}(X) Var(aX+b)=a2Var(X)
-
-
设 Y Y Y是另一个随机变量。
-
E [ X + Y ] = E [ X ] + E [ Y ] \mathbb{E}[X+Y] = \mathbb{E}[X] + \mathbb{E}[Y] E[X+Y]=E[X]+E[Y]
-
Var ( X + Y ) = Var ( X ) + Var ( Y ) 2 cov ( X , Y ) \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) 2\text{cov}(X,Y) Var(X+Y)=Var(X)+Var(Y)2cov(X,Y)
-
十八、估计器、偏差和方差
Estimators, Bias, and Variance
译者:飞龙
学习成果
-
探索常见的随机变量,如伯努利和二项式分布
-
应用中心极限定理来近似总体参数
-
使用抽样数据对真实的潜在分布进行建模估计
-
使用自助法技术从样本中估计真实总体分布
上次,我们介绍了随机变量的概念:样本的数值函数。在上一讲中,我们的大部分工作是建立概率和统计学的背景。现在我们已经建立了一些关键的思想,我们可以将我们学到的知识应用到我们最初的目标上 - 理解样本的随机性如何影响模型设计过程。
在本讲座中,我们将更深入地探讨将模型拟合到样本的想法。我们将探讨如何用随机变量重新表达我们的建模过程,并利用这种新的理解来引导模型的复杂性。
18.1 常见随机变量
有几种经常出现并且具有有用特性的随机变量情况。以下是我们将在本课程中进一步探讨的情况。括号中的数字是随机变量的参数,这些参数是常数。参数定义了随机变量的形状(即分布)和其值。在本讲座中,我们将更加重点关注加粗的随机变量及其特殊性质,但你应该熟悉下面列出的所有随机变量:
-
伯努利§
-
以概率 p 取值 1,以概率 1-p 取值 0。
-
又称“指示”随机变量。
-
设 X 是一个伯努利§随机变量
-
E [ X ] = 1 ? p + 0 ? ( 1 ? p ) = p \mathbb{E}[X] = 1 * p + 0 * (1-p) = p E[X]=1?p+0?(1?p)=p
- E [ X 2 ] = 1 2 ? p + 0 ? ( 1 ? p ) = p \mathbb{E}[X^2] = 1^2 * p + 0 * (1-p) = p E[X2]=12?p+0?(1?p)=p
-
Var ( X ) = E [ X 2 ] ? ( E [ X ] ) 2 = p ? p 2 = p ( 1 ? p ) \text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = p - p^2 = p(1-p) Var(X)=E[X2]?(E[X])2=p?p2=p(1?p)
-
-
-
二项式(n, p)
-
n n n 独立伯努利§试验中的 1 的数量。
-
设 Y Y Y是一个二项式(n, p)随机变量。
-
Y Y Y的分布由二项式公式给出,我们可以写成 Y = ∑ i = 1 n X i Y = \sum_{i=1}^n X_i Y=∑i=1n?Xi?,其中:
-
X i X_i Xi?是第 i i i次试验成功的指示。如果第 i i i次试验成功,则 X i = 1 X_i = 1 Xi?=1,否则为 0。
-
所有的 X i X_i Xi?都是独立同分布的伯努利§。
-
-
E [ Y ] = ∑ i = 1 n E [ X i ] = n p \mathbb{E}[Y] = \sum_{i=1}^n \mathbb{E}[X_i] = np E[Y]=∑i=1n?E[Xi?]=np
-
Var ( X ) = ∑ i = 1 n Var ( X i ) = n p ( 1 ? p ) \text{Var}(X) = \sum_{i=1}^n \text{Var}(X_i) = np(1-p) Var(X)=∑i=1n?Var(Xi?)=np(1?p)
- X i X_i Xi?是独立的,所以对于所有的 i, j, Cov ( X i , X j ) = 0 \text{Cov}(X_i, X_j) = 0 Cov(Xi?,Xj?)=0。
-
-
-
有限值集上均匀分布
-
每个值的概率是 1 / (可能的值的数量)。
-
例如,一个标准/公平的骰子。
-
-
单位区间(0, 1)上均匀分布
- 密度在(0, 1)上为 1,在其他地方为 0。
-
正态( μ , σ 2 \mu, \sigma^2 μ,σ2)
- f ( x ) = 1 σ 2 π exp ? ( ? 1 2 ( x ? μ σ ) ?? 2 ? ) f(x) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left( -\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{\!2}\,\right) f(x)=σ2π?1?exp(?21?(σx?μ?)2)
18.1.1 例子
假设你根据 20 次抛硬币中得到的正面数量赢得现金。如果第 i i i次抛硬币得到正面,则令 X i = 1 X_i = 1 Xi?=1,否则为 0。你会选择哪种支付策略?
A. Y A = 10 ? X 1 + 10 ? X 2 Y_A = 10 * X_1 + 10 * X_2 YA?=10?X1?+10?X2?
B. Y B = ∑ i = 1 20 X i Y_B = \sum_{i=1}^{20} X_i YB?=∑i=120?Xi?
C. Y C = 20 ? X 1 Y_C = 20 * X_1 YC?=20?X1?
解决方案
设 X 1 , X 2 , . . . X 20 X_1, X_2, ... X_{20} X1?,X2?,...X20?是 20 个独立同分布的伯努利(0.5)随机变量。由于 X i X_i Xi?是独立的,对于所有的 i , j i, j i,j对, Cov ( X i , X j ) = 0 \text{Cov}(X_i, X_j) = 0 Cov(Xi?,Xj?)=0。另外,由于 X i X_i Xi?是伯努利(0.5),我们知道 E [ X ] = p = 0.5 \mathbb{E}[X] = p = 0.5 E[X]=p=0.5和 Var ( X ) = p ( 1 ? p ) = 0.25 \text{Var}(X) = p(1-p) = 0.25 Var(X)=p(1?p)=0.25。我们可以计算每种情况的如下内容:
| A. Y A = 10 ? X 1 + 10 ? X 2 Y_A = 10 * X_1 + 10 * X_2 YA?=10?X1?+10?X2? | B. Y B = ∑ i = 1 20 X i Y_B = \sum_{i=1}^{20} X_i YB?=∑i=120?Xi? | C. Y C = 20 ? X 1 Y_C = 20 * X_1 YC?=20?X1? | |
|---|---|---|---|
| 期望 | E [ Y A ] = 10 ( 0.5 ) + 10 ( 0.5 ) = 10 \mathbb{E}[Y_A] = 10 (0.5) + 10(0.5) = 10 E[YA?]=10(0.5)+10(0.5)=10 | E [ Y B ] = 0.5 + . . . + 0.5 = 10 \mathbb{E}[Y_B] = 0.5 + ... + 0.5 = 10 E[YB?]=0.5+...+0.5=10 | E [ Y C ] = 20 ( 0.5 ) = 10 \mathbb{E}[Y_C] = 20(0.5) = 10 E[YC?]=20(0.5)=10 |
| 方差 | Var ( Y A ) = 1 0 2 ( 0.25 ) + 1 0 2 ( 0.25 ) = 50 \text{Var}(Y_A) = 10^2 (0.25) + 10^2 (0.25) = 50 Var(YA?)=102(0.25)+102(0.25)=50 | Var ( Y B ) = 0.25 + . . . + 0.25 = 5 \text{Var}(Y_B) = 0.25 + ... + 0.25 = 5 Var(YB?)=0.25+...+0.25=5 | Var ( Y C ) = 2 0 2 ( 0.25 ) = 100 \text{Var}(Y_C) = 20^2 (0.25) = 100 Var(YC?)=202(0.25)=100 |
| 标准差 | SD ( Y A ) ≈ 7.07 \text{SD}(Y_A) \approx 7.07 SD(YA?)≈7.07 | SD ( Y B ) ≈ 2.24 \text{SD}(Y_B) \approx 2.24 SD(YB?)≈2.24 | SD ( Y C ) = 10 \text{SD}(Y_C) = 10 SD(YC?)=10 |
正如我们所看到的,所有的情景都有相同的期望值,但方差不同。方差越大,风险和不确定性就越大,因此“正确”的策略取决于个人的偏好。你会选择“最安全”的选项 B,最“冒险”的选项 C,还是介于两者之间的选项 A?
18.2 样本统计
今天,我们已经广泛讨论了总体;如果我们知道随机变量的分布,我们可以可靠地计算期望、方差、随机变量的函数等。请注意:
-
总体的分布描述了随机变量在所有感兴趣的个体中的行为。
-
样本的分布描述了随机变量在来自总体的特定样本中的行为。
然而,在数据科学中,我们经常无法接触到整个总体,因此我们不知道它的分布。因此,我们需要收集一个样本,并使用它的分布来估计或推断总体的属性。在这种情况下,我们可以从总体中取几个大小为
n
n
n的样本(一个简单的方法是使用df.sample(n, replace=True)),并计算每个样本的均值。在抽样时,我们做出(很大的)假设,即我们从总体中均匀随机地进行有放回抽样;我们样本中的每个观察都是从我们的总体分布中独立同分布地随机抽取的随机变量。请记住,我们的样本均值是一个随机变量,因为它取决于我们随机抽取的样本!另一方面,我们的总体均值只是一个数字(一个固定的值)。
18.2.1 样本均值
考虑一个从具有均值𝜇和标准差𝜎的总体中抽取的 i.i.d.样本 X 1 , X 2 , . . . , X n X_1, X_2, ..., X_n X1?,X2?,...,Xn?。我们定义样本均值为 X ˉ n = 1 n ∑ i = 1 n X i \bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i Xˉn?=n1?i=1∑n?Xi?
样本均值的期望值由以下公式给出: E [ X ˉ n ] = 1 n ∑ i = 1 n E [ X i ] = 1 n ( n μ ) = μ \begin{align} \mathbb{E}[\bar{X}_n] &= \frac{1}{n} \sum_{i=1}^n \mathbb{E}[X_i] \\ &= \frac{1}{n} (n \mu) \\ &= \mu \end{align} E[Xˉn?]?=n1?i=1∑n?E[Xi?]=n1?(nμ)=μ??
方差由以下公式给出: Var ( X ˉ n ) = 1 n 2 Var ( ∑ i = 1 n X i ) = 1 n 2 ( ∑ i = 1 n Var ( X i ) ) = 1 n 2 ( n σ 2 ) = σ 2 n \begin{align} \text{Var}(\bar{X}_n) &= \frac{1}{n^2} \text{Var}( \sum_{i=1}^n X_i) \\ &= \frac{1}{n^2} \left( \sum_{i=1}^n \text{Var}(X_i) \right) \\ &= \frac{1}{n^2} (n \sigma^2) = \frac{\sigma^2}{n} \end{align} Var(Xˉn?)?=n21?Var(i=1∑n?Xi?)=n21?(i=1∑n?Var(Xi?))=n21?(nσ2)=nσ2???
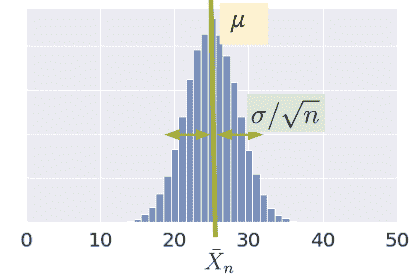
X ˉ n \bar{X}_n Xˉn?根据中心极限定理(CLT)呈正态分布。
18.2.2 中心极限定理
在Data 8和之前的讲座中,你遇到了中心极限定理(CLT)。这是一个强大的定理,用于从一系列较小的样本中估计具有均值 μ \mu μ和标准差 σ \sigma σ的总体的分布。中心极限定理告诉我们,如果一个大小为 n n n的 i.i.d 样本很大,那么样本均值的概率分布大致正态,均值为 μ \mu μ,标准差为 σ n \frac{\sigma}{\sqrt{n}} n?σ?。更一般地,任何提供统计量粗略分布并且不需要总体分布的定理对于数据科学家来说都是有价值的!这是因为我们很少对总体了解很多。
重要的是,中心极限定理假设我们样本中的每个观察都是从总体的分布中抽取的 i.i.d。此外,中心极限定理仅在 n n n“大”时才准确,但什么样的“大”样本量取决于特定的分布。如果一个总体高度对称和单峰,我们可能只需要 n = 20 n=20 n=20;如果一个总体非常倾斜,我们需要更大的 n n n。如果有疑问,可以对样本均值进行自举,并查看自举分布是否呈钟形。像 Data 140 这样的课程会对这个想法进行详细的探讨。
要了解更详细的演示,请查看onlinestatbook。
18.2.3 使用样本均值估计总体均值
现在假设我们想使用样本均值来估计总体均值,例如,加州大学本科生的平均身高。通常我们可以收集一个单一样本,其中只有一个平均值。但是,如果我们碰巧以随机方式抽取了一个具有不同均值或扩展性的样本,会怎么样呢?我们可能会对总体行为有一个偏斜的看法(考虑极端情况,我们碰巧抽取了相同的值 n n n 次!)。
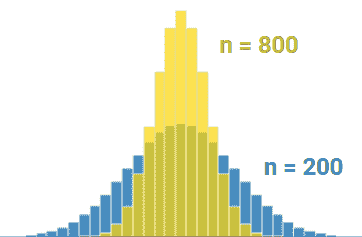
例如,注意这两个分布之间的变化差异,这两个分布在样本大小上是不同的。样本量更大的分布( n = 800 n=800 n=800)比样本量较小的分布( n = 200 n=200 n=200)更紧密地围绕均值。尝试将这些值代入正态分布的标准偏差方程中,以理解这一点!
应用中心极限定理使我们能够理解所有这些并解决这个问题。通过抽取许多样本,我们可以考虑样本分布在数据的多个子集中的变化。这使我们能够近似总体的属性,而无需调查每个成员。
鉴于这种潜在的差异,我们还要考虑所有可能的样本均值的平均值和扩展性,以及这对 n n n 应该有多大的影响。对于每个样本量,样本均值的期望值是总体均值: E [ X ˉ n ] = μ \mathbb{E}[\bar{X}_n] = \mu E[Xˉn?]=μ。我们称样本均值是总体均值的无偏估计量,并将在下一讲中更多地探讨这个想法。
Data 8 Recap: 平方根定律
平方根定律(Data 8)指出,如果将样本量增加一个因子,标准偏差将减少该因子的平方根。 SD ( X n ˉ ) = σ n \text{SD}(\bar{X_n}) = \frac{\sigma}{\sqrt{n}} SD(Xn?ˉ?)=n?σ? 如果我们有更大的样本量,样本均值更有可能接近总体均值。
18.3 预测和推断
在课程的这一阶段,我们花了大量时间研究模型。几周前我们首次介绍了建模的概念时,是在预测的背景下:使用模型对未知数据进行准确预测。我们构建模型的另一个原因是更好地理解我们周围复杂的现象。推断是使用模型推断特征和响应变量之间真实的基本关系的任务。例如,如果我们正在处理一组房屋数据,预测可能会问:根据房屋的属性,它值多少钱?推断可能会问:当地公园对房屋价值有多大影响?
推断的一个主要目标是仅凭随机样本对完整数据总体进行推断。为此,我们旨在估计参数的值,这是总体的数值函数(例如,总体均值 μ \mu μ)。我们使用收集的样本来构建统计量,这是随机样本的数值函数(例如,样本均值 X ˉ n \bar{X}_n Xˉn?)。将“p”视为“参数”和“总体”,将“s”视为“样本”和“统计量”是有帮助的。
由于样本代表总体的随机子集,我们生成的任何统计量可能会偏离真实的总体参数,并且可能会有所不同。我们说样本统计量是真实总体参数的估计量。在符号上,总体参数通常称为 θ \theta θ,而其估计量用 θ ^ \hat{\theta} θ^ 表示。
为了回答我们的推断问题,我们旨在构建能够紧密估计总体参数值的估计量。我们通过回答三个问题来评估估计量的“好坏”:
-
我们平均得到参数的正确答案吗?
-
答案有多大的变化?
-
我们的答案与参数有多接近?
18.3.1 建模作为估计
现在我们已经建立了估计量的概念,让我们看看如何将这种学习应用到建模过程中。为此,我们将花一点时间用随机变量的语言来形式化我们的数据收集和模型。
假设我们正在处理一个输入变量 x x x和一个响应变量 Y Y Y。我们假设 Y Y Y和 x x x通过某种关系 g g g相关联;换句话说, Y = g ( x ) Y = g(x) Y=g(x)。 g g g代表一些定义 x x x和 Y Y Y之间基础关系的“普遍真理”或“自然法则”。在下面的图像中, g g g由红线表示。
然而,作为数据科学家,我们无法直接“看到”基础关系 g g g。我们能做的最好的事情就是收集在现实世界中观察到的数据,以尝试理解这种关系。不幸的是,数据收集过程总会存在一些固有的误差(想象一下在科学实验中进行测量时可能遇到的随机性)。我们说每个观察都伴随着一些随机误差或噪声项 ? \epsilon ?。假定这个误差是一个随机变量,期望为 E ( ? ) = 0 \mathbb{E}(\epsilon)=0 E(?)=0,方差为 Var ( ? ) = σ 2 \text{Var}(\epsilon) = \sigma^2 Var(?)=σ2,并且在每个观察中都是独立同分布的。这种随机噪声的存在意味着我们的观察 Y ( x ) Y(x) Y(x)是随机变量。
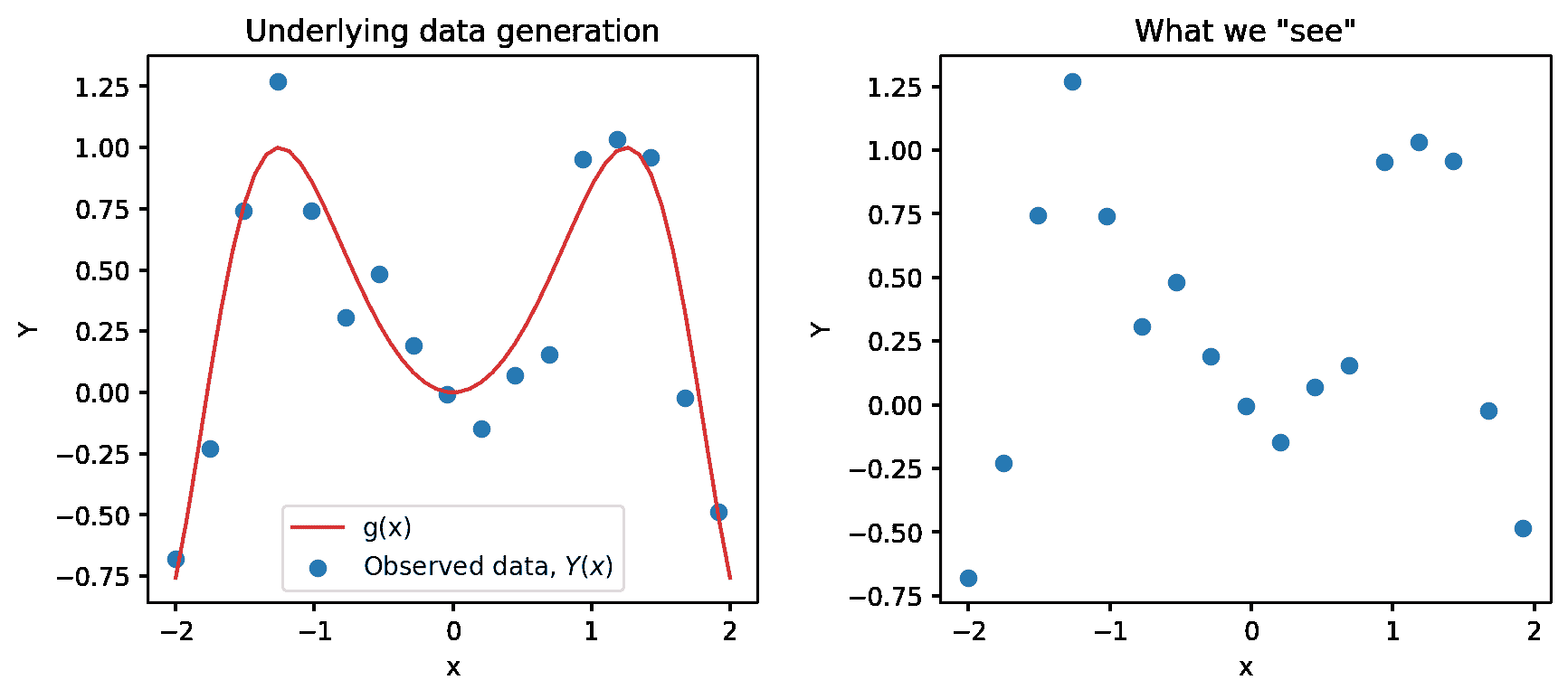
我们只能观察到我们的随机数据样本,用蓝色点表示。从这个样本中,我们想要估计真实关系 g g g。我们通过构建模型 Y ^ ( x ) \hat{Y}(x) Y^(x)来估计 g g g。
真实关系:? g ( x ) \text{真实关系: } g(x) 真实关系:?g(x)
观察到的关系:? Y = g ( x ) + ? \text{观察到的关系: }Y = g(x) + \epsilon 观察到的关系:?Y=g(x)+?
预测:? Y ^ ( x ) \text{预测: }\hat{Y}(x) 预测:?Y^(x)
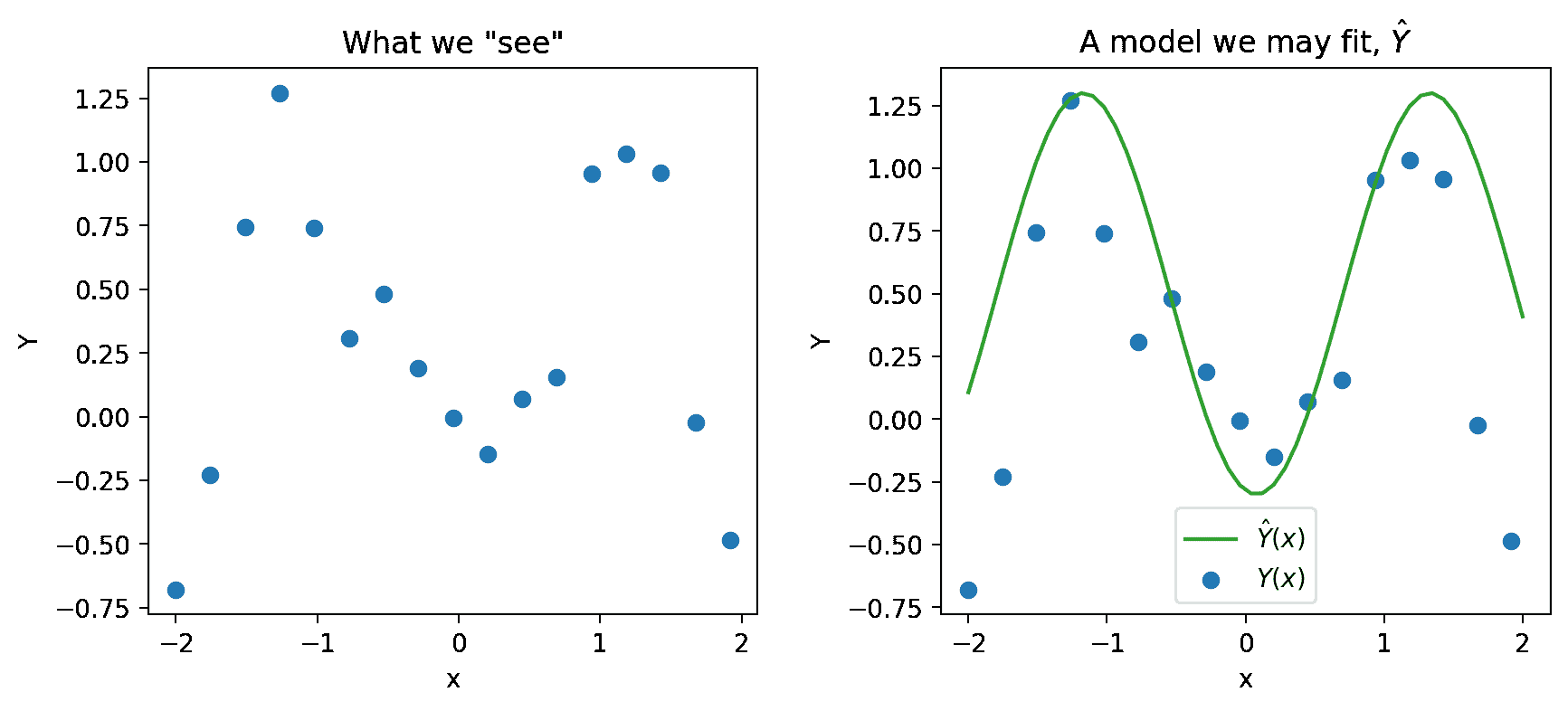
18.3.1.1 估计线性关系
如果我们假设真实关系 g g g是线性的,我们可以将响应表示为 Y = f θ ( x ) Y = f_{\theta}(x) Y=fθ?(x),其中我们的真实关系由 Y = g ( x ) + ? Y = g(x) + \epsilon Y=g(x)+?
f θ ( x ) = Y = θ 0 + ∑ j = 1 p θ j x j + ? f_{\theta}(x) = Y = \theta_0 + \sum_{j=1}^p \theta_j x_j + \epsilon fθ?(x)=Y=θ0?+j=1∑p?θj?xj?+?来建模。
哪些表达式是随机的?
在我们上面的两个方程中,真实关系 g ( x ) = θ 0 + ∑ j = 1 p θ j x j g(x) = \theta_0 + \sum_{j=1}^p \theta_j x_j g(x)=θ0?+∑j=1p?θj?xj?不是随机的,但 ? \epsilon ?是随机的。因此, Y = f θ ( x ) Y = f_{\theta}(x) Y=fθ?(x)也是随机的。
*这个真实关系有真实的、不可观测的参数 θ \theta θ,并且它有随机噪声 ? \epsilon ?,所以我们永远无法观察到真实关系。相反,我们能做的下一个最好的事情就是获得一个样本 X \Bbb{X} X, Y \Bbb{Y} Y的 n n n个观察关系 ( x , Y ) (x, Y) (x,Y),并用它来训练一个模型并获得 θ ^ \hat{\theta} θ^的估计 Y ^ ( x ) = f θ ^ ( x ) = θ 0 ^ + ∑ j = 1 p θ j ^ x j \hat{Y}(x) = f_{\hat{\theta}}(x) = \hat{\theta_0} + \sum_{j=1}^p \hat{\theta_j} x_j Y^(x)=fθ^?(x)=θ0?^?+j=1∑p?θj?^?xj?
哪些表达式是随机的?
在我们上面的估计方程中,我们的样本 X \Bbb{X} X, Y \Bbb{Y} Y是随机的。因此,我们从样本中计算的估计 θ ^ \hat{\theta} θ^也是随机的,所以我们的预测 Y ^ ( x ) \hat{Y}(x) Y^(x)也是随机的。
现在看一下我们的原始方程,我们可以看到它们都有不同的随机来源。对于我们观察到的关系, Y = g ( x ) + ? Y = g(x) + \epsilon Y=g(x)+?, ? \epsilon ?代表测量误差并反映未来的随机性。对于估计模型,我们拥有的数据是从总体中收集的随机样本,因此是过去的随机性。
18.4 自助法重采样(复习)
确定估计量的抽样分布的属性,比如方差,我们需要访问总体,以便我们可以考虑所有可能的样本并计算每个样本的估计。

然而,我们无法访问总体;我们只有来自总体的一个随机样本。如果我们只有一个样本,我们如何考虑所有可能的样本呢?
自助法的想法是将我们的随机样本视为“总体”,并从中进行有放回的重新采样。直观地说,随机样本类似于总体,因此随机重新采样也重新对随机样本进行重新采样。

Bootstrap 重采样是一种估计估计量抽样分布的技术。要执行它,我们可以按照下面的伪代码进行:
collect a random sample of size n (called the bootstrap population)
initiate list of estimates
repeat 10,000 times:
resample with replacement n times from bootstrap population
apply estimator f to resample
store in list
list of estimates is the bootstrapped sampling distribution of f
为什么我们必须进行有放回的重新采样?
给定大小为 n n n的原始样本,我们希望得到与原始样本相同大小 n n n的重新采样。不进行替换的抽样将给我们洗牌后的原始样本。因此,当我们计算像平均值这样的摘要统计时,我们不进行替换的样本将始终具有与原始样本相同的平均值,从而破坏了自助法的目的。
自助法实际上如何代表我们的总体?估计量的自助法抽样分布并不完全匹配该估计量的抽样分布,但通常是接近的。同样,自助法分布的方差通常接近于估计量的真实方差。下面的示例显示了使用样本大小 n = 50 n=50 n=50从已知总体进行不同自助法的结果。**
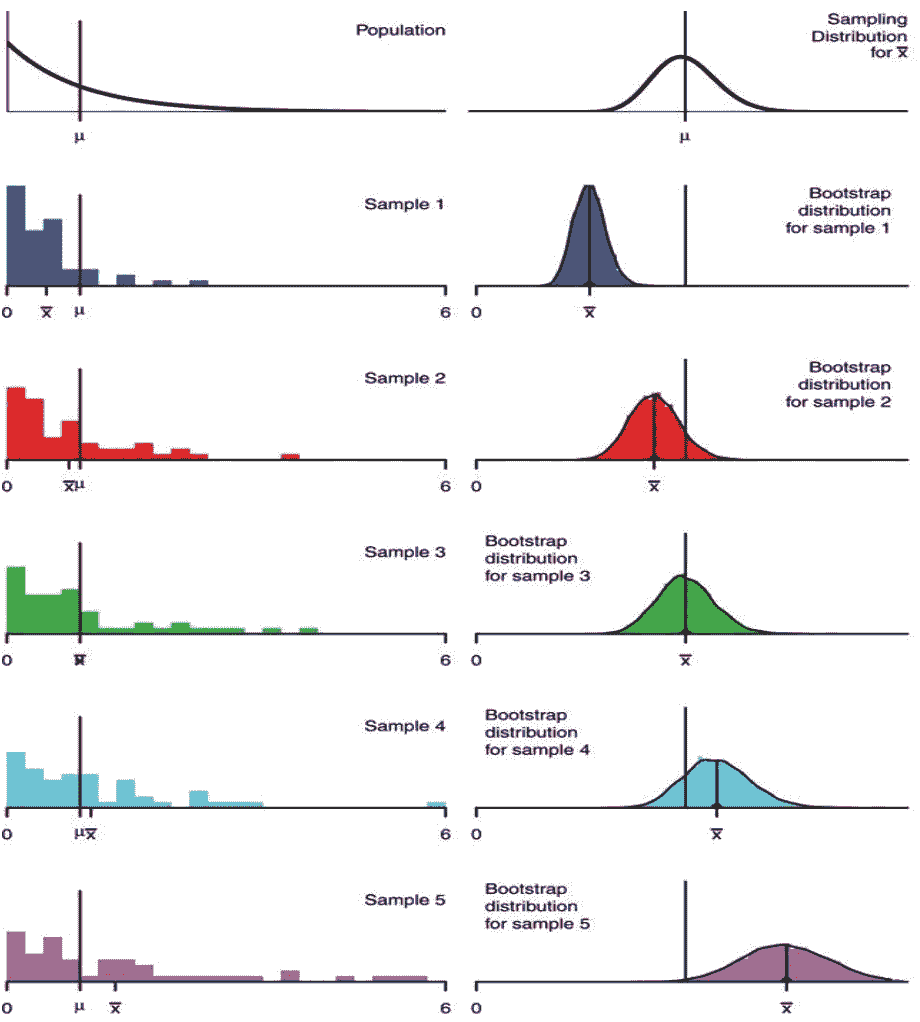
在现实世界中,我们不知道总体分布。自助法分布的中心是应用于我们原始样本的估计量,因此我们无法恢复估计量的真实期望值。我们的自助法分布的质量取决于我们原始样本的质量;如果我们的原始样本不代表总体,自助法几乎没有用处。
需要注意的一点是,自助法通常对某些统计量(如中位数或其他基于分位数的统计量)效果不佳,这些统计量严重依赖于较大样本中的少数观察结果。自助法无法克服小样本作为推断依据的弱点。事实上,对于非常小的样本,最好是做出额外的假设,比如参数族。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 修改字符串(c++题解)
- 释放创造力:可视化页面渲染引擎在低代码开发平台的应用
- 鸿鹄电子招投标系统:源码级别解析电子招投标的精髓
- MVC环境搭建
- 聚焦QCon:小红书邀你一起探讨高性能网关、LLM 推理加速
- java使用AES加密数据库解密
- 了解JavaScript的执行环境及作用域
- 新能源汽车的三电指的是什么,作用有什么区别。
- 连接MySQL时报2003 - Can‘t connect to MySQL server on ‘xxx.xxx.xxx.xxx‘(10060 “Unknown error“)
- 数据库原理课程考试网站设计-计算机毕业设计源码78952