代码随想录算法训练营Day5 | 454.四数相加||、383.赎金信、35.三个之和、18.四数之和
LeetCode 454 四数相加 ||

本题思路:
如果使用暴力的话就是 4 层 for 循环,这个时间复杂度就是 O(n^4) 了。
所以我们可以使用 map ,来解决这道题,和之前的两数之和一样,之前是 遍历一个,存进去一个。 如果我们将 nums1 和 nums[2],每一个位置上的和,都存入 map 集合,然后再判断 target - (nums3[i]+nums4[j]) 的值是否存在于 map 中,如果在,就计数器 count = count + map.get(这个值)。 注意:累加的是这个值存在的次数。
下面就利用 示例1 画一个图来更好的理解下这个思路: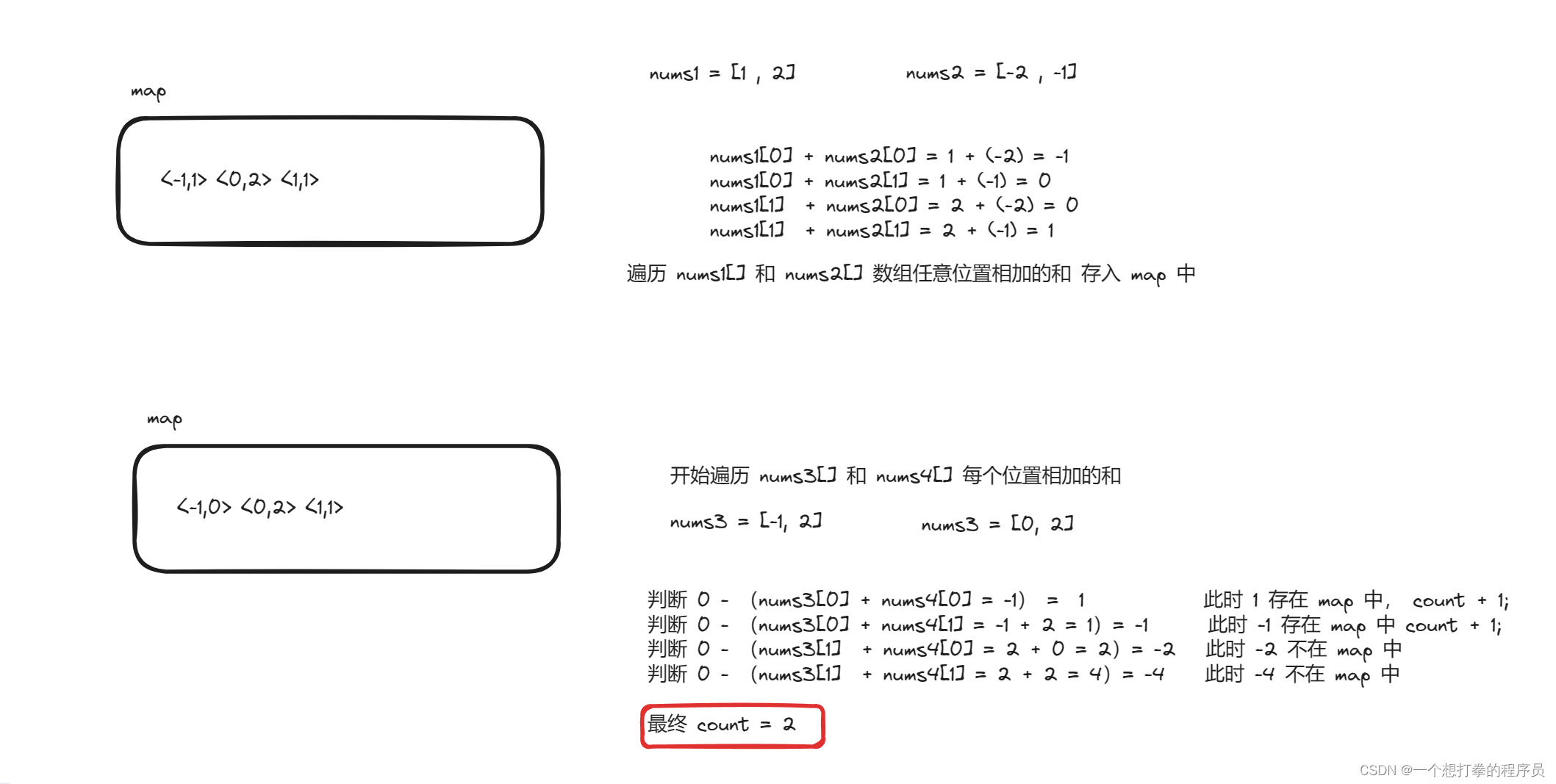
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
// 本题思路返回有多少个元素,需要一个计数器 count,碰到符合的条件就 count++
Map<Integer,Integer> map = new HashMap();
// 将 nums1 nums2,每个位置都相加 存放到集合 map 中
for(int i = 0; i < nums1.length; i++){
for(int j = 0; j < nums2.length; j++){
map.put(nums1[i] + nums2[j], map.getOrDefault(nums1[i] + nums2[j],0) + 1);
}
}
int count = 0;
// 利用 0 - (nums3 + nums4) 的值 等于0 的情况,来判断有多个符合条件的四元组
for(int i = 0; i < nums3.length; i++){
for(int j = 0; j < nums4.length; j++){
if(map.containsKey(0 - (nums3[i] + nums4[j]))){
count = count + map.get(0 - (nums3[i] + nums4[j]));
}
}
}
return count;
}
}
注意点:就是 count 不是 count++;
LeetCode 383 赎金信

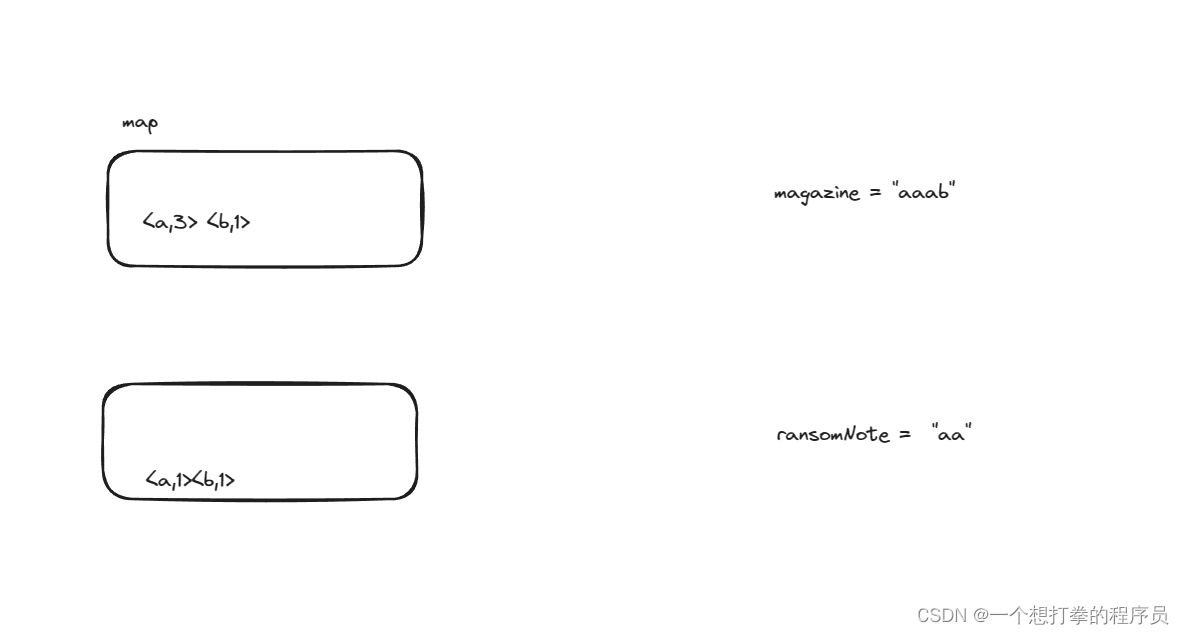
本题思路:判断 ransomNote 是否能由 magazine 组成,说明 magazine 包含 ransomNode,magazine 的范围大一点,所以我们可以很容易想到使用 map , 将 magazine 中的元素全部存入到 map 中,并记录每个元素存在的次数。 然后便利 ransomNode 中的每个元素,判断 magazine 中是否都存在,如果有 一个 不存在就返回 false。如果存在,但是次数已经为 0 ,也返回 false。否则就 次数减 0
下面用一个图来分析下 示例 1,以便更好理解上述思路
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
Map<Character,Integer> map = new HashMap();
for(int i = 0; i < magazine.length(); i++){
map.put(magazine.charAt(i),map.getOrDefault(magazine.charAt(i),0)+1);
}
for(int i = 0; i < ransomNote.length(); i++){
// 如果 magazine 里面没有 ransomNote 或者 这个元素存在此处已经 为 0 ,则返回false
if( !map.containsKey(ransomNote.charAt(i)) || map.get(ransomNote.charAt(i)) == 0){
return false;
}
map.put(ransomNote.charAt(i),map.get(ransomNote.charAt(i)) -1);
}
return true;
}
}
本题其实用数组的情况下会更好,使用 map 的空间复杂夫会更高于一些(在数量大的时候就能体现出来),因为 map 底层会维护 红黑树 或者 链表等。以下是使用数组的代码。
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
// shortcut
if (ransomNote.length() > magazine.length()) {
return false;
}
// 定义一个哈希映射数组
int[] record = new int[26];
// 遍历
for(char c : magazine.toCharArray()){
record[c - 'a'] += 1;
}
for(char c : ransomNote.toCharArray()){
record[c - 'a'] -= 1;
}
// 如果数组中存在负数,说明ransomNote字符串总存在magazine中没有的字符
for(int i : record){
if(i < 0){
return false;
}
}
return true;
}
}
LeetCode 35 三数之和

注意点:
- 要去重,不能出现重复的三元组。所以在每次 i 遍历的时候,都要先进行去重操作
- 进行 nums[left] 和 nums[right] 去重的时候,要先保存记录,再进行去重操作。
- 对 nums[left] 和 nums[right] 进行去重的时候,一定要保证 left < right (比如 000000 这种情况就会出现下标越界的情况)
本题思路:使用双指针来解决,一个指针 i 从 数组起始位置开始,如果 nums[i] = nums[i-1] ,i 往后走。然后定义一个 left = i + 1, right = nums.length - 1, 判断 nums[i] + nums[left] + nums[right] == 0 , 如果等于 0 就保存这三个数,并且, 在这判断过程中,有可能 nums[left] = nums[left+1], nums[right] = nums[right-1] , 此时 left 也要往后走一个,直到不等为止,right同理往前。
为了方便理解这个思路,利用示例 1:画个图来分析下代码

- 循环 i = 0的时候如下图
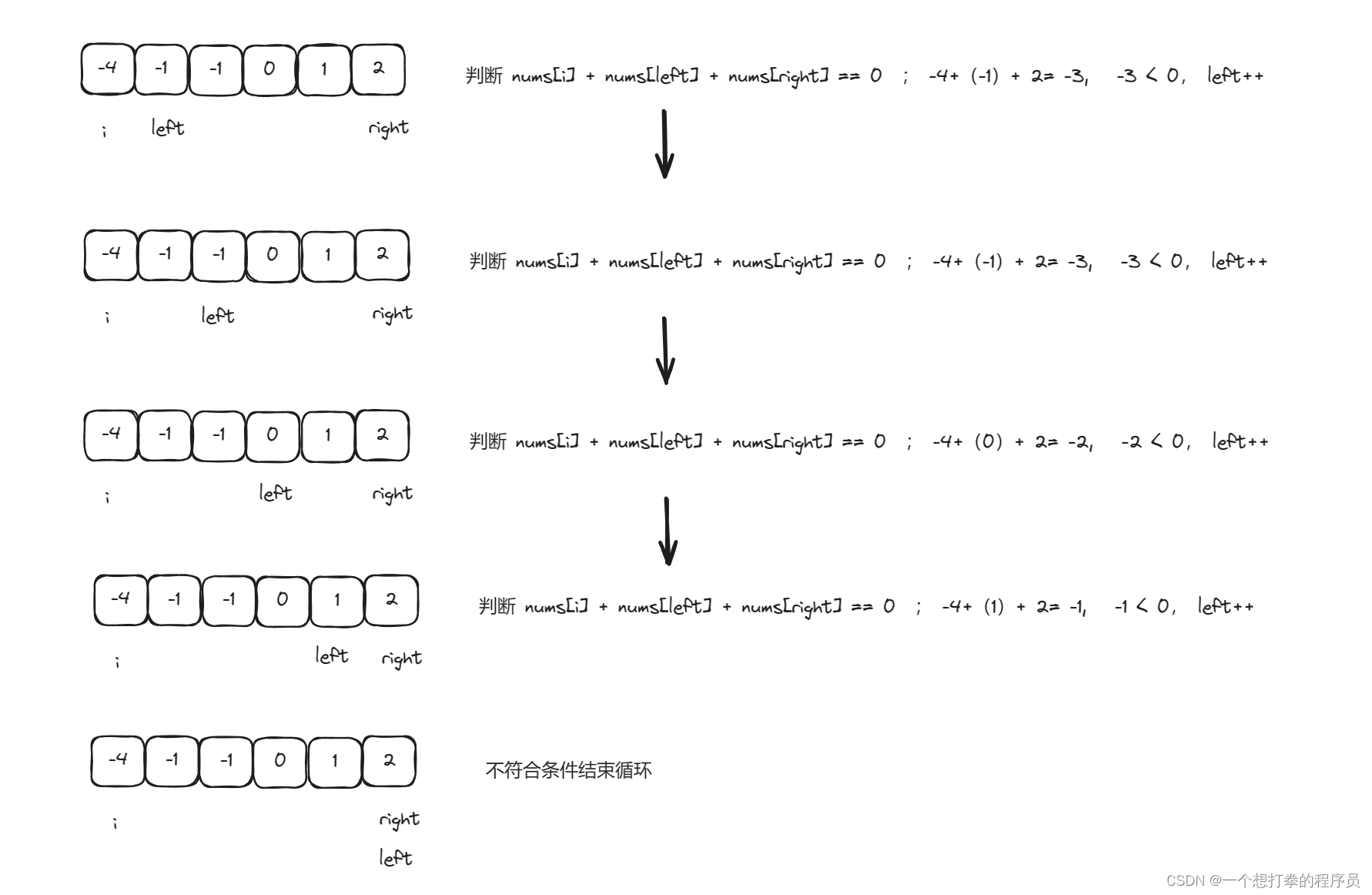
- 循环 i = 1的时候

- 循环 i = 2的时候, 此时由于 nums[2] = nums[1]了,所以需要跳过这一循环
- 循环 i = 3的时候

- 循环 i = 4的时候

- 循环 i = 5的时候不符合条件,结束。
- 所以最终结果为 【-1,-1,2】【-1,0,-1】
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList();
for (int i = 0; i < nums.length; i++) {
// 如果第一个元素就 大于 > 0, 直接返回 res;
if (nums[i] > 0) {
return res;
}
// 去重 nums[i],这里不能用 nums[i] == nums[i+1] (-1,-1,0)
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.length - 1;
while (left < right) {
// 开始判断
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0) {
List<Integer> list = new ArrayList();
list.add(nums[i]);
list.add(nums[left]);
list.add(nums[right]);
res.add(list);
// 进行去重 nums[left] 和 nums[right]
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
left++;
right--;
} else if (sum < 0) {
left++;
} else {
right--;
}
}
}
return res;
}
LeetCode 18 四数之和

本题思路: 延用三数之和的思想。在外层 在套 一个 for 循环。用来遍历第一个数字,里面就和 三数之和的逻辑一样了。
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
// 思路:和三数之和一样,使用双指针,只不过外面套一层 for 循环
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList();
for(int k = 0; k < nums.length; k++){
// 先进行剪枝操作
if(nums[k] > target && nums[k] > 0){
break;
}
// 进行去重操作
if( k > 0 && nums[k] == nums[k-1]){
continue;
}
for(int i = k+1; i < nums.length; i++){
int left = i + 1;
int right = nums.length - 1;
// 先进行剪枝操作
if( nums[k] + nums[i] > target && nums[k] + nums[i] > 0 ){
break;
}
// 进行去重操作
if( i > k + 1 && nums[i] == nums[i-1]){
continue;
}
while(left < right){
int sum = nums[k] + nums[i] + nums[left] + nums[right];
if(sum < target){
left++;
}else if(sum > target){
right--;
}else{
// 相同记录下来
List<Integer> list = new ArrayList();
list.add(nums[k]);
list.add(nums[i]);
list.add(nums[left]);
list.add(nums[right]);
res.add(list);
// 开始去重 nums[left] 和 nums[right]
while(left < right && nums[left] == nums[left+1]){
left++;
}
while(left < right && nums[right] == nums[right-1]){
right--;
}
left++;
right--;
}
}
}
}
return res;
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【力扣4行代码解题】572另一棵树的子树 | C++
- 【华为数据之道学习笔记】6-1什么是数据服务
- 分布式调用链对比(pinpoint、skywalking、jaeger、zipkin等)
- Linux查看用户过期时间及禁用用户登陆
- 实现公共字段自动填充 (苍穹外卖)
- 自动化我选DrissionPage,弃用Selenium
- Java数据结构
- return、break、continue用法和区别(C/C++)
- Jtti:mysql如何连接别人的数据库?
- C++系列第九篇 数据类型下篇 - 复合类型(指针高级应用)