函数递归的总结回顾
函数递归的本质就是其名字——递与归。先递出去, 再收回来。
而递归的思想就是为了让一个复杂的问题变成一个简单的问题
按照我目前的理解,函数递归有两点很重要。一个是它的限定条件,另一个就是函数体内“自调”(就是自我调用语句,这里我叫它“自调”)的位置。
递归的逻辑问题
限定条件很好理解,一个函数递归,如果没有限定条件,将会陷入死递归。
而“自调”的位置对于整体的函数逻辑有巨大的影响。为了能够更加理解这种影响,我在这里放上一个例子:
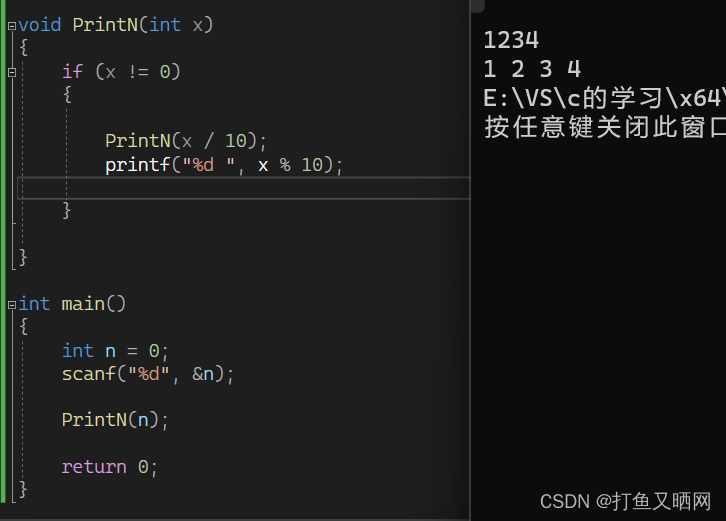
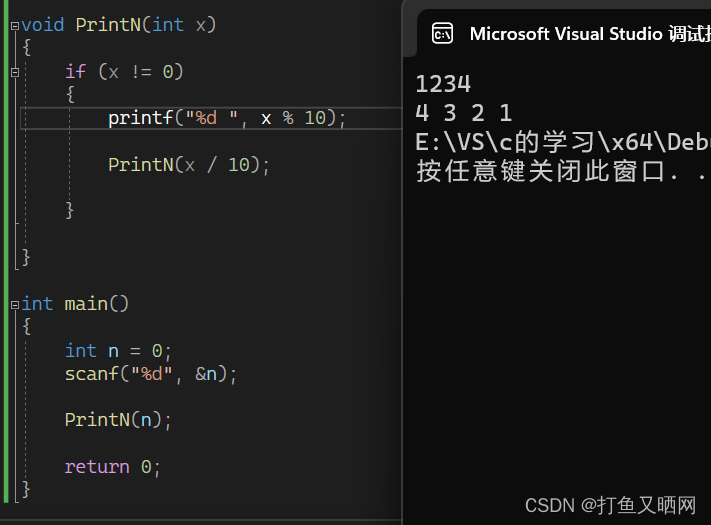
这两张图分别是printf 在“自调”前后的运行图。可以看到结果有很大的差异。原因就是因为逻辑问题,下面是这两个程序的逻辑图?
这是printf在“自调”语句后的逻辑
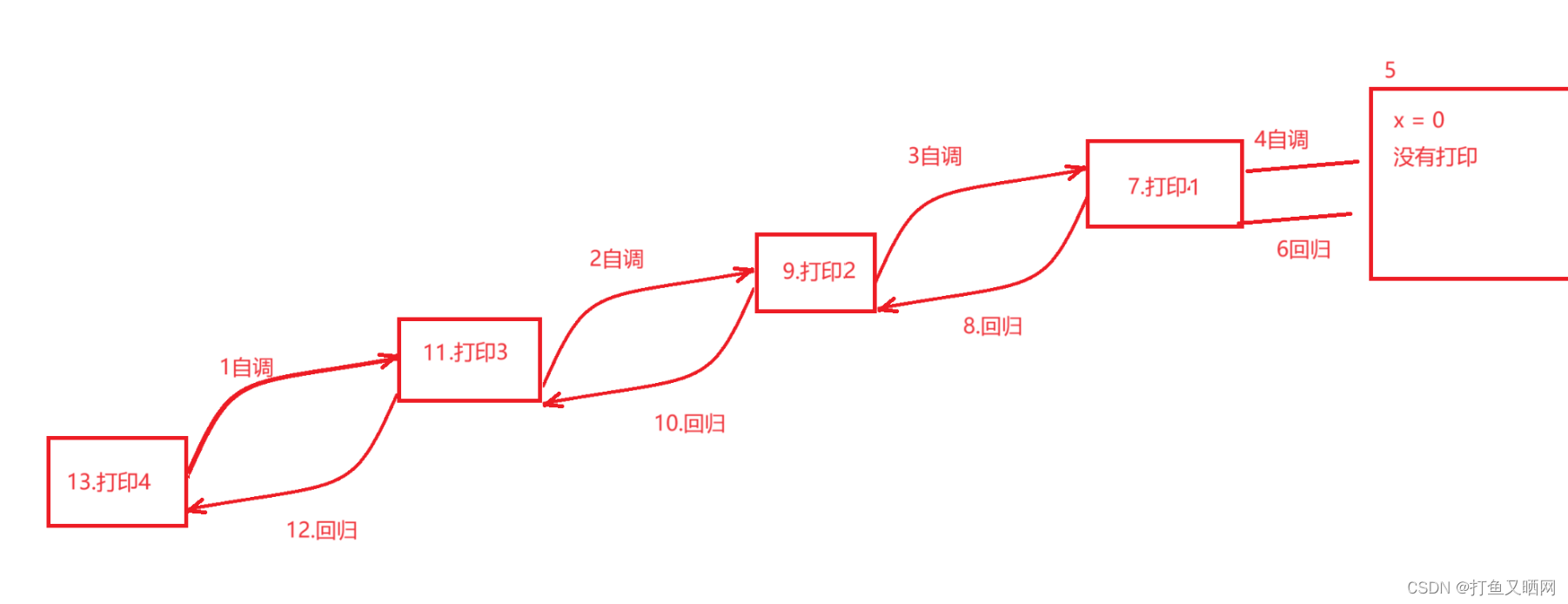
这是printf在“自调”语句前的逻辑
?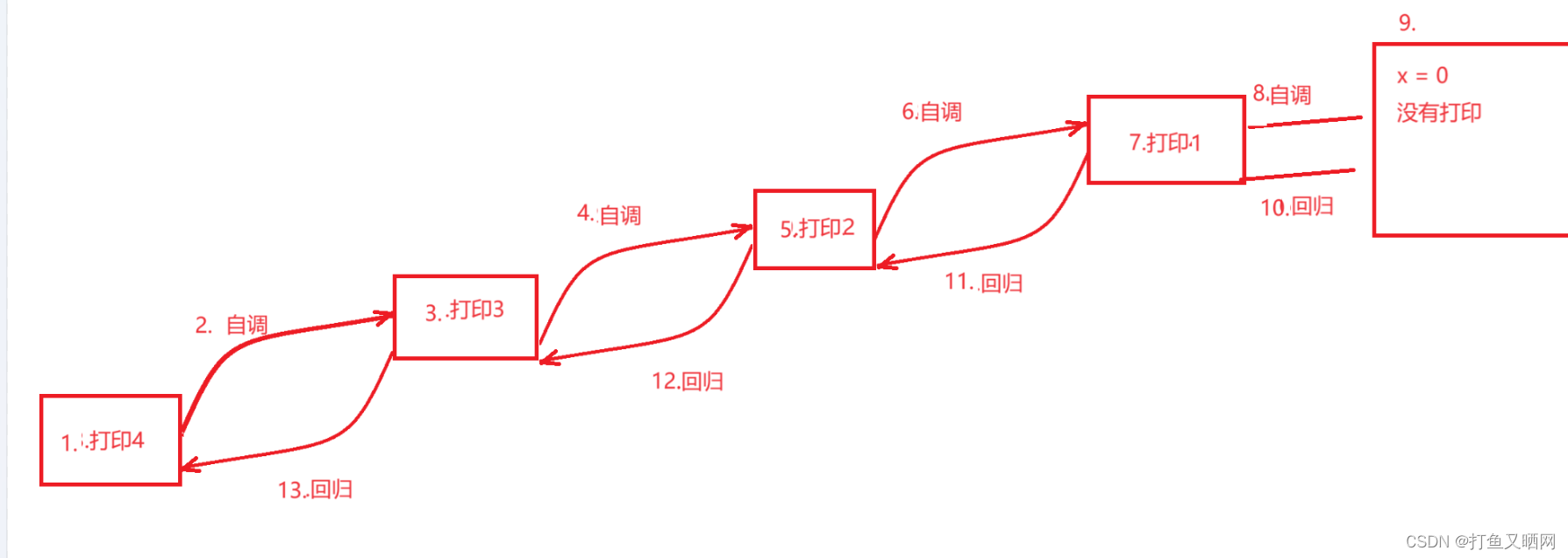
?两个的函数逻辑有差异,导致最后打印的结果完全不同。
其实,在函数递归中,在“自调”语句之前的句子在“递出去”的部分执行,按照从外向内的顺序执行逻辑执行。而在“自调”语句之后的句子在“收回来”的部分执行,按照从内向外的执行逻辑执行。
这就是我理解的递归函数逻辑问题。
递归与迭代
什么是迭代?
迭代与递归是不同的。递归就像套娃,一层一层的。而迭代就是所谓的循环。
递归因为是函数进行层层调用,而函数的调用需要开辟栈帧空间。所以虽然递归相对来说写起来很简便,但是递归的开销是大于迭代的,如果递归的程度很深,那么更是容易造成栈溢出的现象。比如斐波那契数列就不便于使用递归。假如我们给一个计数器,用来计算一共的函数调用的次数:
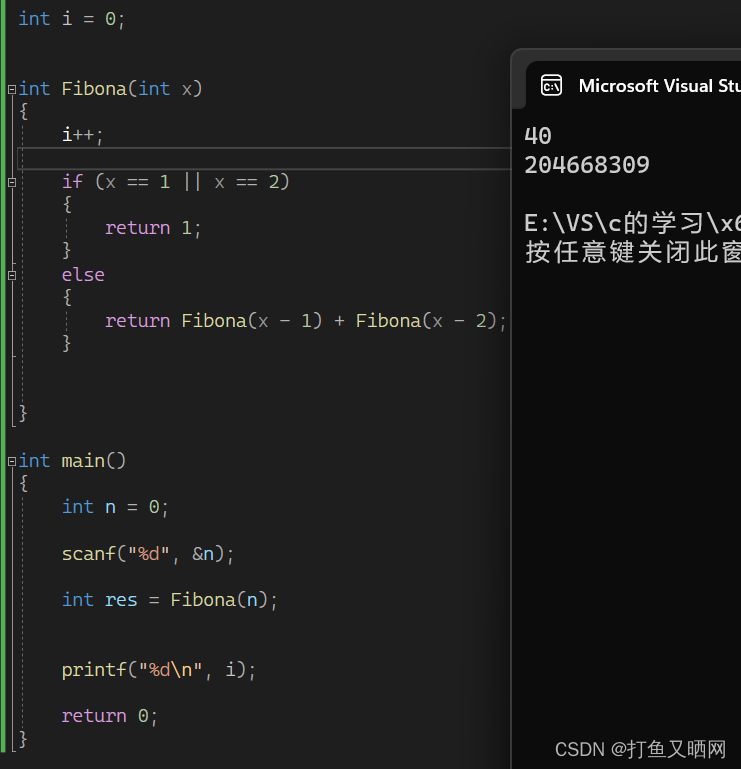 ?
?
可以看到,当n为40时,函数就已经被调用了2亿多次。 这个数字太大了,而如果使用迭代来计算,就少之又少了。?
所以, 有的问题看似可以使用递归进行简化,但其实递归并不可取,需要仔细分析。
青蛙跳台阶问题
一只青蛙跳台阶,每次只能跳一阶或者两阶,请问想要跳到n阶,青蛙有几种跳法?
这个问题就是斐波那契问题。

如图,想要跳到第n阶,那么有两种可能,一种是从第n - 2阶跳两阶到n, 一种是从n - 1阶跳一阶到n。
假设跳到n阶有fn种方法,则跳到n - 2阶就有f n-2种方法。跳到n - 1阶就有f n-1种方法
那么青蛙跳到第n 阶就有f n = f n-1 + f n-2种方法。
由此可以知道,这是一个斐波那契数列问题。
代码如下:
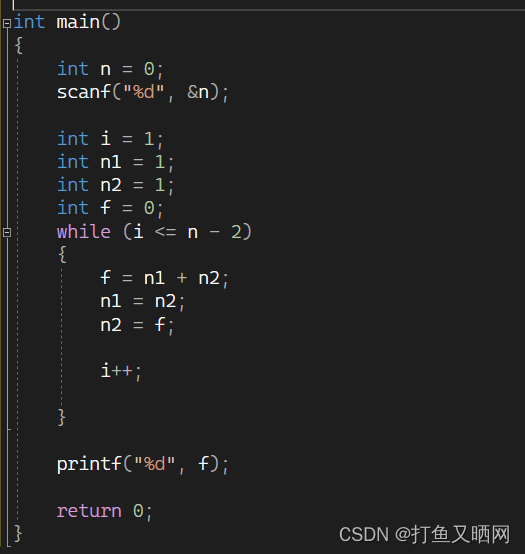 ?
?
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 003-90-08【RDD-Transformation】虎跑泉旁人家大闺女小红用GPT学习Spark: filter 和 map
- c#跳转界面文字乱码解决方案
- 探秘淘宝店铺所有商品API接口:一键获取海量数据,引领电商数据革命
- 规则引擎Drools的入门使用
- 【并发编程】wait/notify
- C++ 递归函数 详细解析——C++日常学习随笔
- C语言进阶——数据结构之链表
- C语言初阶——分支和循环语句
- FaFu--练习复盘--3
- DRF-源码解析-4-限流的流程:drf的限流源码,drf流量控制流程,drf如何流量控制