力扣hot100 最长递增子序列 线性DP 贪心 二分

Problem: 300. 最长递增子序列

💖 动态规划

思路

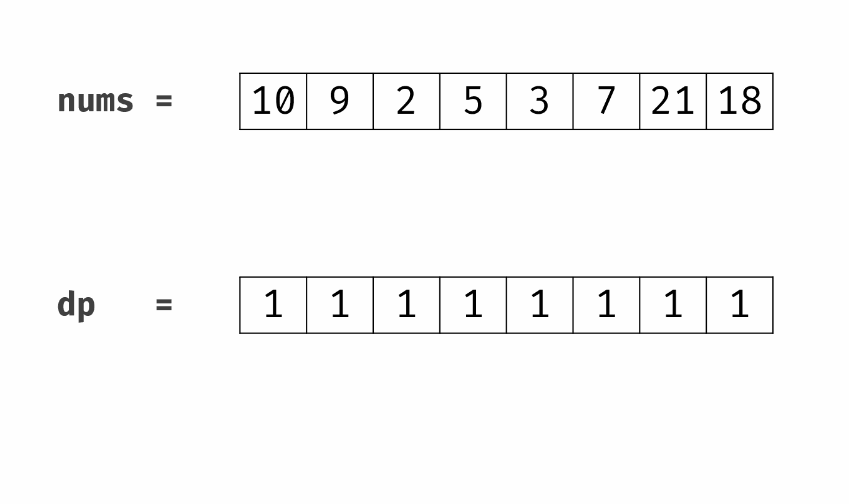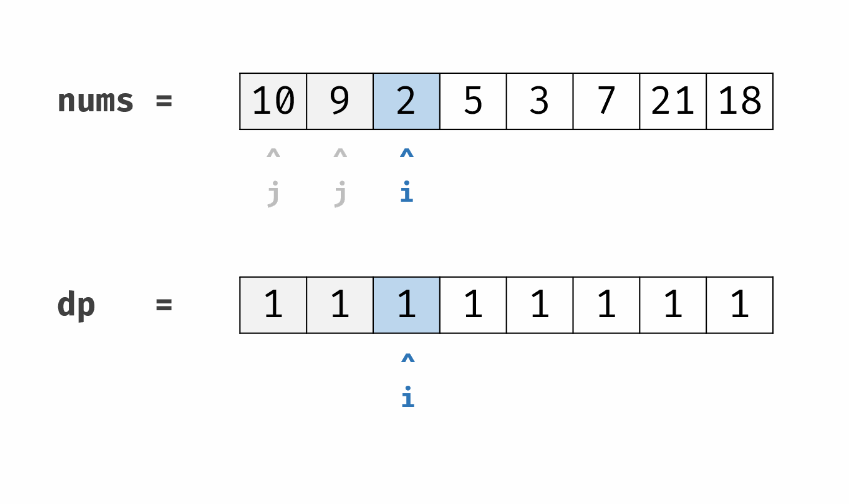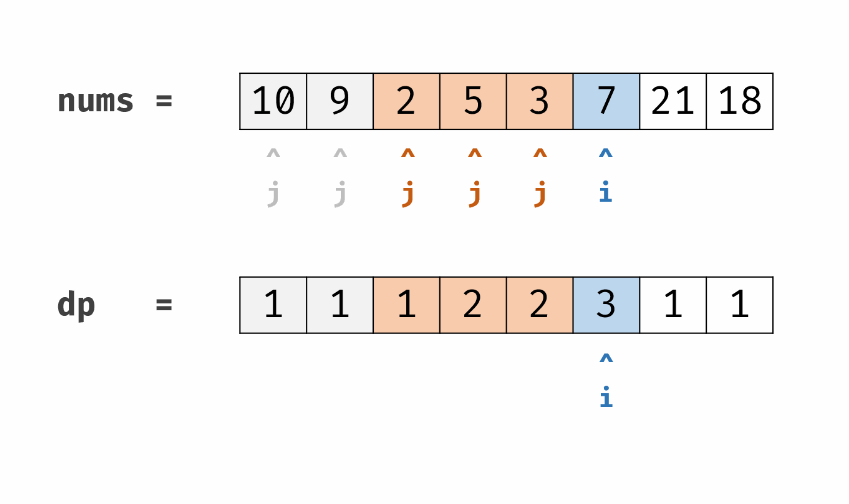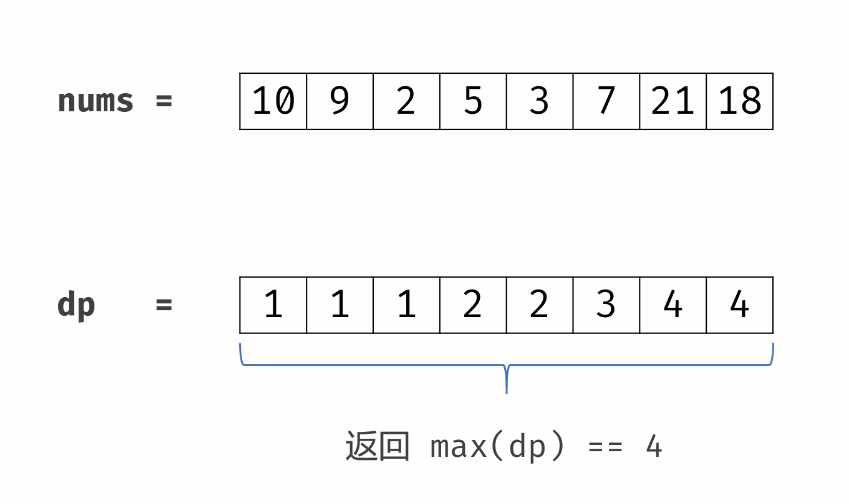
复杂度

时间复杂度: $O(n^2)$

空间复杂度: $O(n)$

Code

class Solution {
	public int lengthOfLIS(int[] nums)
	{
		int n = nums.length;
		int[] f = new int[n + 1];// f[i] 表示以 nums[i] 结尾的最大上升子序列长度
		int ans = 0;
		for (int i = 0; i < n; i++)
		{
			f[i] = 1;//以自己为结尾，初始化长度为 1
			for (int j = 0; j < i; j++)
				if (nums[i] > nums[j])// 在 i 前边找到一个严格比自己小的元素，接上去（+1）
					f[i] = Math.max(f[i], f[j] + 1);
			ans = Math.max(ans, f[i]);//答案即是以任意元素结尾的最大上升子序列的最大值
		}
		return ans;
	}
}

---

💖 贪心 + 二分

思路

👨?🏫 参考题解

复杂度

时间复杂度: $O(n\log n)$

空间复杂度: $O(n)$

Code

class Solution {
	public int lengthOfLIS(int[] nums)
	{
		int n = nums.length;
		int[] tail = new int[n + 1];// tail[i] 表示子序列长度为 i 的最小元素值
		int ans = 0;
		for (int x : nums)
		{
			int l = 0;
			int r = ans;
//			找到 tail[i-1] < x < tail[i] 的位置，x就可以把 tail[i] 替换掉
//			换而言之，就是找到第一个  >  x 的 tail[i] 的 i (upperBound)
			while (l < r)
			{
				int m = l + r >> 1;
				if (tail[m] < x)
					l = m + 1;
				else
					r = m;
			}
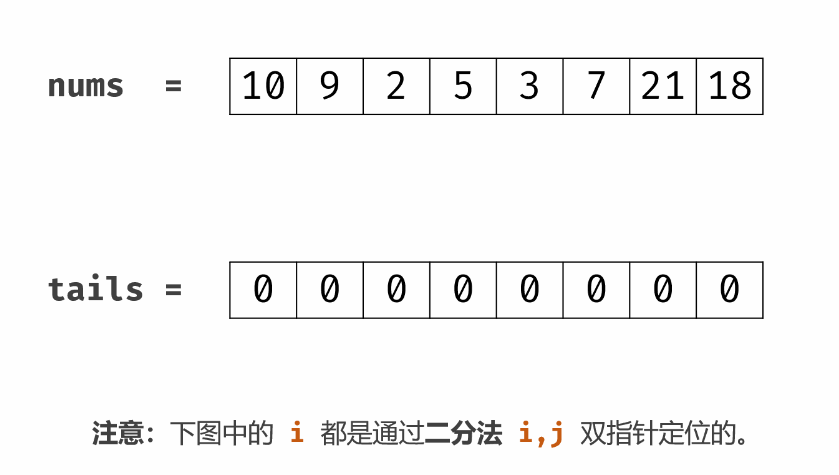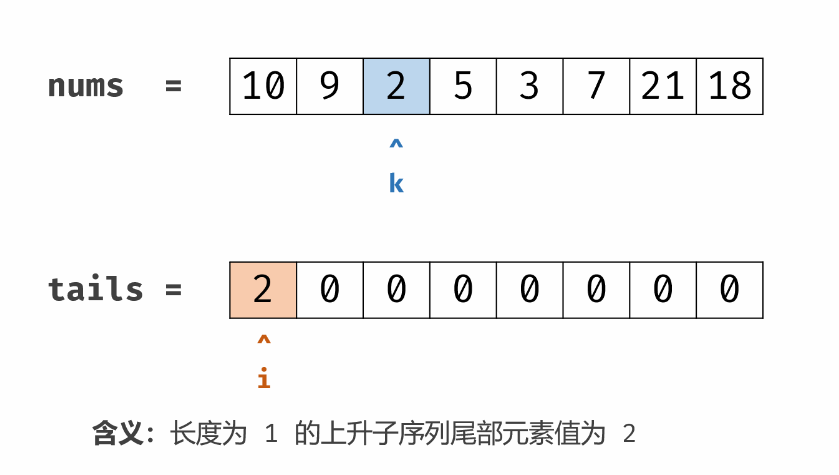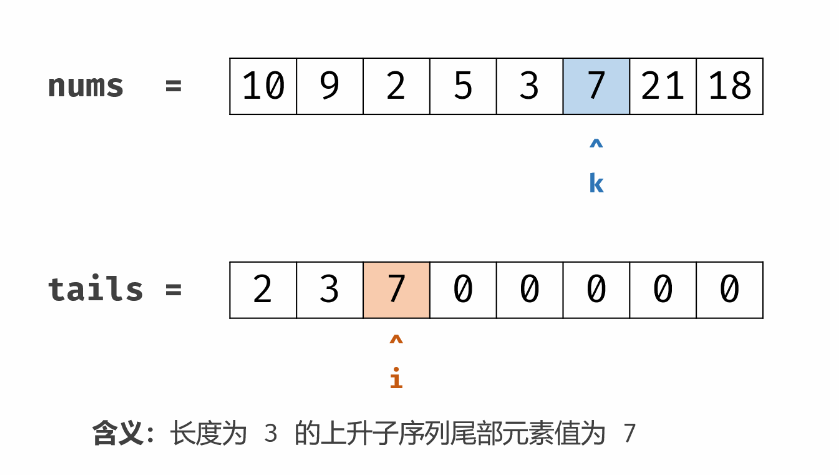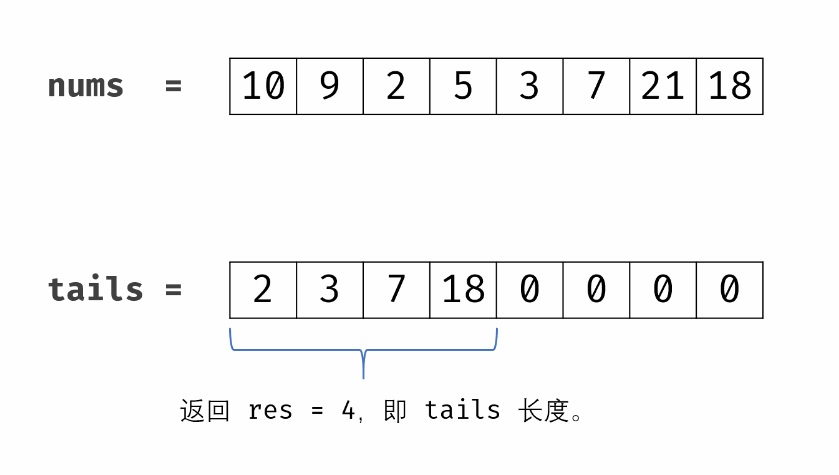
			tail[l] = x;
			// ans == l 说明目前tail数组的元素都比当前的 num 要小 因此最长子序列的长度可以增加了 
			if (ans == l)
				ans++;
		}
		return ans;
	}
}