数据科学的统计基础

在本文的范围内；

1.总体和抽样概念

2. 变量的类型

3. 量表的类型

4. 集中趋势的测量

5、集中分散措施

我将介绍对数据科学家来说很重要的基本统计概念，例如：祝您阅读愉快。

二、总体和抽样概念

????????从数据科学家的角度来看，

????????人口（主要人口）；这是关于要处理的主题的具有共同特征的所有观察结果。定义总体的指标（平均值、中位数等）称为参数。

????????样本;?它是将用于数据科学研究的人群的子集。描述样本的指标（平均值、中位数等）称为统计数据。

????????从总体中选择样本的过程称为抽样。

Sampling Methods | Types, Techniques & Examples

????????当今世界数据的快速增长是不争的事实。既然如此，在数据科学过程中对人群进行研究几乎是不可能的。即使在大数据项目中，也会对样本进行分析，建立模型并获得总体推断。

????????从总体中选择的样本必须能够代表总体，这一点非常重要，这样才能使分析和推论可靠且无偏见。因此，开发了不同的采样方法。其中一些方法是：

????????简单随机抽样：在这种方法中，所有观察结果都有相同的机会。

• 由于它是随机的，因此样本通常没有偏见，但具有代表性。
• 当没有关于总体的先验信息时可以使用它。

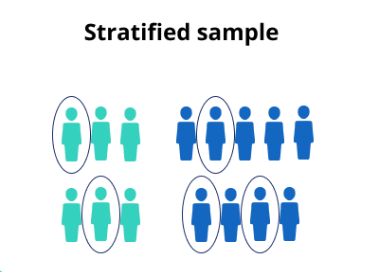
????????分层抽样：将总体分为几层，每层按照其在总体中的权重比例进行简单随机抽样。

• 当我们获得有关群体中各层的初步信息时，就会使用它。
• 它可以用于不平衡的数据集。（例如欺诈、垃圾邮件检测）
• 层内变异性低，层间变异性高。
• 注：某些情况下，可以将变量按区间划分，进行分层抽样。例如，如果我们要分析各个年龄段人群的样本，可以将年龄范围分为几个部分，然后进行分层选择。

????????聚类抽样：选择不是根据观察结果而是根据它们所连接的聚类进行选择。

• 虽然簇内变异性较高，但簇间变异性较低。例如，很难对居住在 100 个不同社区的人们进行调查。因此，通过简单随机抽样方法从这些邻域（集群）中选择x，并对居住在所选邻域中的所有个体进行调查。

三、变量的类型

????????不同观察结果之间存在差异的特征称为“变量”。变量根据其结构分为数值（定量）和分类（定性）两种。

????????数值变量：这些变量可以用数字和数量来解释。例如;?身高、体重、年龄、成功分数……等。我们可以测量数值变量之间的差异。

????????分类变量：这些是可以分类的变量。例如;?性别（男孩女孩）、肤色、国家/地区……等。我们无法衡量分类变量之间的差异，但我们可以观察到存在差异。

四、?量表的类型

分类变量的量表类型：名义变量和序数变量

数值变量的尺度类型：范围和比率

标称：

• 我们可以判断两个变量是否彼此不同。
• 我们无法评论它们之间差异的大小和方向。
• 颜色：我们可以说红色和黄色不同，但不能说它们更大或更小。

序数：

• 我们可以确定两个变量之间存在差异以及这种差异的方向。
• 英语水平：初级、中级、高级。
• 可以说阿里的英语水平比艾谢还要高。但阿里的英语水平比艾谢高......?我们不能说它那么高。

十二月：

• 我们可以谈谈两个变量之间差异的方向和大小。（今天天气比昨天暖和）
• 具有一定起点（相对零）并且其单位之间的差异相等的标尺称为等距标尺。
• 它是一种量表，其中 0 并不表示不存在。（日期、温度测量单位、..）
• 两点之间的距离有意义，但比率没有意义。（不能根据比例做出-5度比5度冷-1倍之类的评论。）

奥兰：

• 它可以用于以前使用过的秤类型的所有情况，因此它是最强大的秤类型。
• 0 表示真实不存在。
• 变量可以按比例比较。（Ali的体重是Ayse体重的2倍）
• 速度、收入、身高、体重……

五、集中趋势的测量

集中趋势的度量是总结数据集的统计数据。当我们有各种值并且我们想用单个值汇总这些值时使用它。
例如;?我们有一个班级学生数学考试的成绩，校长询问班级的情况，我们不用一一统计每个人的成绩，而是用一个值来总结所有成绩，用平均值来总结集中趋势测量并表示班级的平均数学成绩为 75。

平均的 ：

它是系列中数字的总和除以系列中元素的数量所获得的值。平均值受到异常值的影响，因此不稳健。

• 它适用于连续且正态分布的数据。

中位数：

它是数据集从小到大排序的中间值。如果数据集中有偶数个元素，则通过取中间两个值的平均值来找到中位数。
与均值不同，中值不依赖于数据集中的所有值。因此，异常值对中位数的影响较小。

• 当分布偏斜或存在异常值时，中位数比平均值更能衡量集中趋势。
• 它可用于具有连续分布、有序分布和偏态分布的数据。

在正态分布的数据中，均值和中位数彼此靠近地位于中间。

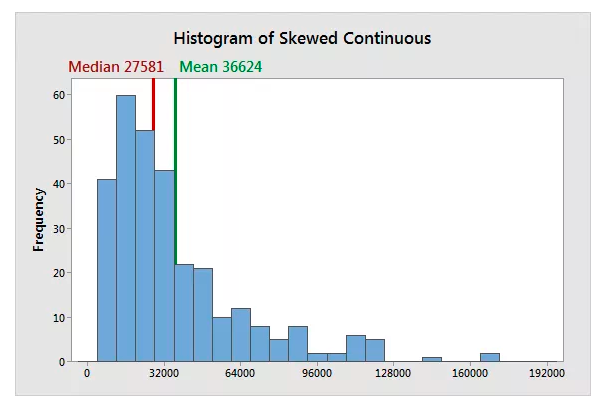
在偏态分布的数据中，均值会受到异常值的影响并接近它们。

模组：

它是数据集中最常观察到的值。对于分类变量，它是条形图中最长的值。在连续变量中，可以将其确定为概率分布的峰值。

• 它可用于分类、序数和连续（概率分布）数据。

何时使用哪一个？

• 当分布对称时，均值、中位数和众数相等。在这种情况下，通常选择平均值，因为它是通过考虑所有观测值来计算的。
• 当数据集有倾斜时，使用中位数更为合适。
• 对于序数数据，可以使用中位数或众数。
• 在分类数据中，使用众数。

六、集中分散措施

????????集中趋势的测量并不总是足以解释数据集。还需要显示观测单元彼此之间距离的测量，称为“中心分散测量”。

????????例如，在下面的图表中，我们看到两个数据集具有相同的平均值但分布不同。仅根据平均值来解释这两个数据集是不正确的。

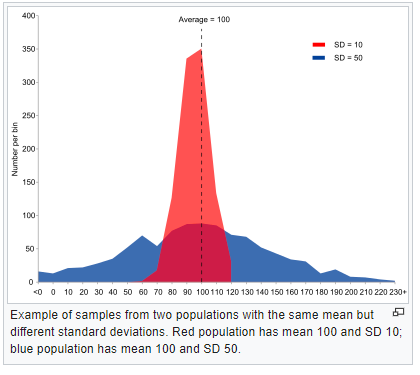
6.1 范围?

????????它是一系列中最大值和最小值之间的差。（范围=最大-最小）

• 由于它始终关注极值，因此对异常值观察很敏感，因此它可能并不总是最佳选择。
• 随着数据集大小的增加，范围往往会增加，因此它只能用于大小相似的数据集中的比较目的。

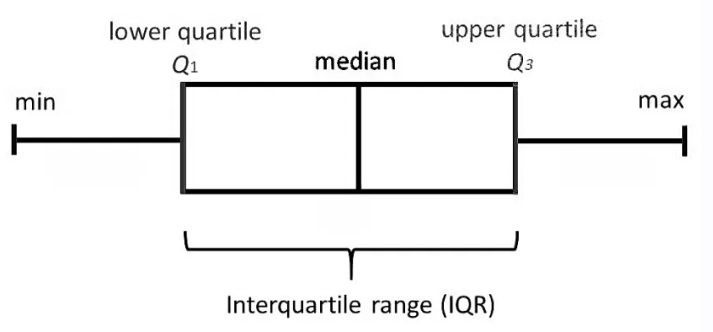
6.2 IQR（四分位距）：

????????它是排序数据集的中间一半。计算方法是用第三季度减去第一季度。（IQR = Q3 — Q1）

• 它比范围更强。

6.3 标准差?

????????标准差是对平均值偏差的一般衡量。

????????在标准正态分布中，68% 的数据落在平均值的一个标准差范围内。

• 小标准差表明数据组中的值彼此接近。标准差大表明数据组中的值彼此相差很远。
• 标准差越小，意味着与平均值的偏差越小，风险越小；如果它很大，则表明偏离平均值和风险程度。
• 例如，您需要紧急货物，您需要选择一家公司，您需要在平均交货时间相等的两家公司之间做出选择。在这种情况下，选择标准差较低的公司会降低风险。

6.4 方差：

????????方差只是标准差的平方。换句话说，它是与平均值的偏差的平方的平均值。

6.5 偏度?

????????偏度是分布偏离正态分布程度的度量，由“皮尔逊偏度系数”计算：

数据科学统计：Python 统计

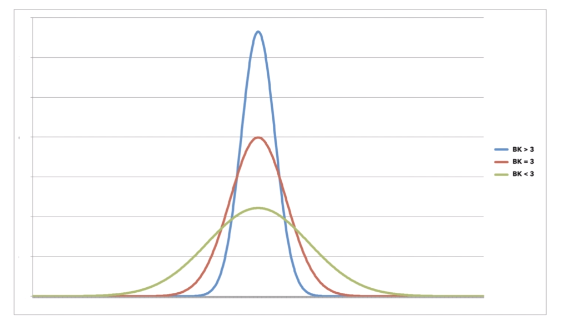
6.6 峰度?

????????平坦度是平坦度或尖度的度量。

数据科学统计：Python 统计

????????在本文中，我们从基本概念的层面介绍了构成数据科学基础的统计学。请参阅其他文章，我将讨论在数据科学中更为重要的统计问题。