【二叉树5】二叉树深度+节点个数+平衡总结

求高度：后序遍历；求深度，前序遍历。

高度就像楼房，节点在几层楼，深度就像地下室，在地下几层。

求高度用后序遍历就像往上走必须经过较低的楼层，先走了一层楼才能去到二楼。

求深度相反，必须经过b1，才能到b2。

递归法是一种通过将问题分解为更小、相似的子问题并逐步解决的编程和数学技术。在递归法中，一个函数在执行过程中调用自身。递归是一种解决问题的有效而简洁的方法，但需要注意正确设置递归的终止条件，以避免无限递归。

递归法和迭代法是两种不同的问题解决方法，它们之间的主要区别在于解决问题的方式和控制流结构。

1. 解决问题的方式：

   • 递归法： 通过将一个问题分解为更小、相似的子问题，并通过调用自身来解决这些子问题。递归通常使用递归函数来描述问题的解决方法。
   • 迭代法： 通过迭代（循环）的方式，从问题的初始状态逐步向解决目标推进。迭代通常使用循环结构，而不是函数的嵌套调用。

2. 控制流结构：

   • 递归法： 递归使用函数调用的方式，每次函数调用都会生成一个新的函数栈帧，存储局部变量和执行状态。递归的控制流通常是通过函数调用栈来管理的。
   • 迭代法： 迭代使用循环结构，通过重复执行一段代码块来解决问题。控制流在每次循环迭代中前进，直到达到循环终止条件。

3. 终止条件：

   • 递归法： 递归函数必须有一个或多个终止条件，确保问题规模足够小，可以直接解决。终止条件是避免无限递归的关键。
   • 迭代法： 迭代使用循环终止条件来决定何时退出循环。终止条件通常与问题的规模或目标状态有关。

1.二叉树深度

求二叉树深度思路：我们知道求深度是从上往下的计算深度，或者从下往上计算高度，这里使用后续计算高度，也就是说根节点高度就是最大深度。而高度就是一层一层节点的高度的叠加。

递归

解读：左右子树高度可能不相同，分别求左右子树高度求最大值。

迭代

代码分析：这是利用双端队列存放节点，根据先进先出原则，按照左右中的顺序放入节点。

每次放入根节点的左右子节点就将depth+1，记录高度也就是深度。

2.节点个数

递归法

迭代法

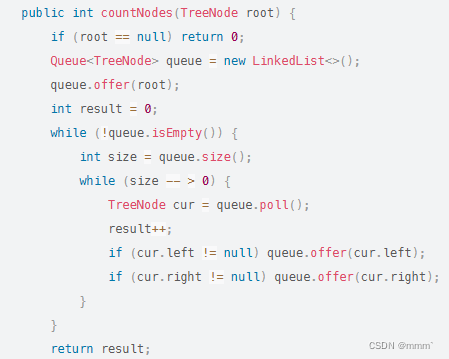
3.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点?的左右两个子树的高度差的绝对值不超过 1 。

也就是判断每一个节点的左右子树高度差不超过1。

代码分析：这里对于左子树和右子树求高度容易理解，return是返回当前中节点高度，这就是为什么要用后序遍历求高度的原因。这样就可以层层往上求所有节点左右子树的高度。