双指针算法

常?的双指针有两种形式，?种是对撞指针，?种是左右指针。
对撞指针：?般?于顺序结构中，也称左右指针。

• 对撞指针从两端向中间移动。?个指针从最左端开始，另?个从最右端开始，然后逐渐往中间逼近。

• 对撞指针的终?条件?般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循环），也就是：

  • left == right （两个指针指向同?个位置）
  • left > right （两个指针错开）

快慢指针：?称为?兔赛跑算法，其基本思想就是使?两个移动速度不同的指针在数组或链表等序列 结构上移动。这种?法对于处理环形链表或数组?常有?。 其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使?快慢指针的思想。快慢指针的实现?式有很多种，最常?的?种就是：

• 在?次循环中，每次让慢的指针向后移动?位，?快的指针往后移动两位，实现?快?慢。
  

移动零（easy)

链接地址：移动零

算法思路

在本题中，我们可以??个 cur 指针来扫描整个数组，另?个 dest 指针?来记录?零数序列的最后?个位置。根据 cur 在扫描的过程中，遇到的不同情况，分类处理，实现数组的划分。 在 cur 遍历期间，使 [0, dest] 的元素全部都是?零元素， [dest + 1, cur - 1] 的元素全是零。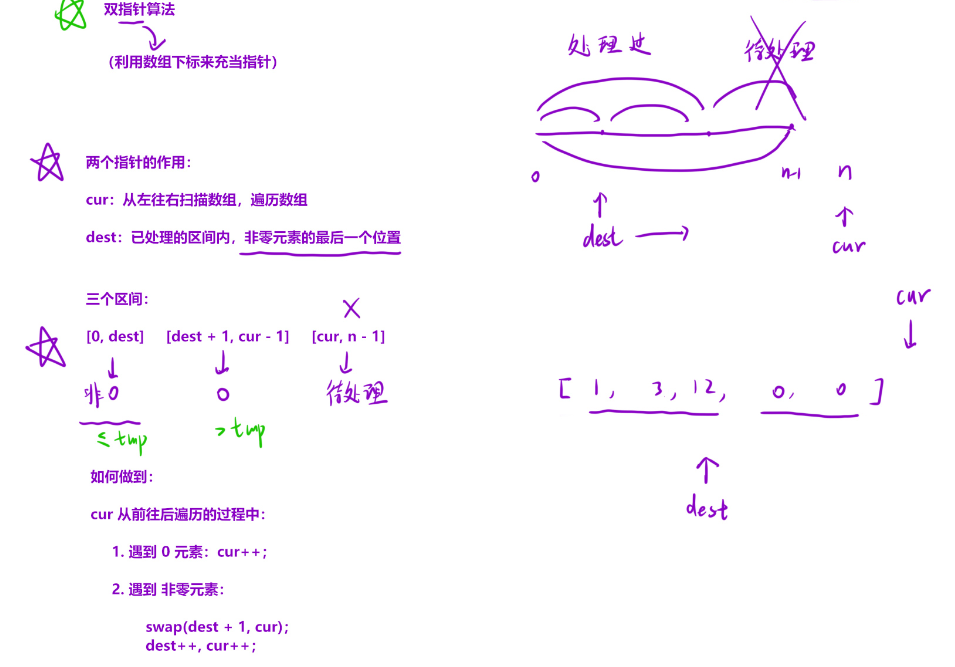

算法流程

1. 初始化 cur = 0 （?来遍历数组）， dest = -1 （指向?零元素序列的最后?个位置，因为刚开始我们不知道最后?个?零元素在什么位置，因此初始化为 -1 ）
2. cur 依次往后遍历每个元素，遍历到的元素会有下?两种情况：
   1. 遇到的元素是 0 ， cur 直接 ++ 。因为我们的?标是让 [dest + 1, cur - 1] 内的元素全都是零，因此当 cur 遇到 0 的时候，直接 ++ ，就可以让 0 在 cur - 1的位置上，从?在 [dest + 1, cur - 1] 内；
   2. 遇到的元素不是 0 ， dest++ ，并且交换 cur 位置和 dest 位置的元素，之后让cur++ ，扫描下?个元素。
3. 因为 dest 指向的位置是?零元素区间的最后?个位置，如果扫描到?个新的?零元素，那么它的位置应该在 dest + 1 的位置上，因此 dest 先?增 1 ；
4. dest++ 之后，指向的元素就是 0 元素（因为?零元素区间末尾的后?个元素就是0 ），因此可以交换到 cur 所处的位置上，实现 [0, dest] 的元素全部都是?零元素， [dest + 1, cur - 1] 的元素全是零。
   

代码

class Solution {
    public void moveZeroes(int[] nums) {
        int cur = 0;
        int dest = -1; // 指向非0的最后一位数
        while(cur < nums.length) {
            if(nums[cur] != 0) {
                swap(nums, ++dest, cur);
            }
            cur++;
        }
    }
    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

复写零（easy)

链接地址：复写零

算法思路

如果「从前向后」进?原地复写操作的话，由于 0 的出现会复写两次，导致没有复写的数「被覆盖掉」。因此我们选择「从后往前」的复写策略。
但是「从后向前」复写的时候，我们需要找到「最后?个复写的数」，因此我们的?体流程分两步：
i. 先找到最后?个复写的数；
ii. 然后从后向前进?复写操作。

算法流程

代码

class Solution {
    public void duplicateZeros(int[] arr) {
        // 1. 找到最后一个数
        int cur = 0, dest = -1, n = arr.length;
        while(cur < n) {
            if(arr[cur] == 0) {
                dest += 2;
            }else {
                dest++;
            }
            if(dest >= n - 1) {
                break;
            }
            cur++;
        }
        // 处理边界情况
        if(dest == n) {
            arr[n - 1] = 0;
            cur--;
            dest -= 2;
        }
        // 从后往前开始覆盖
        while(cur >= 0) {
            if(arr[cur] == 0) {
                arr[dest--] = 0;
                arr[dest --] = 0;
            }else {
                arr[dest--] = arr[cur];
            }
            cur--;
        }
    }
}

快乐数（mid)

题目链接：快乐数

算法思路

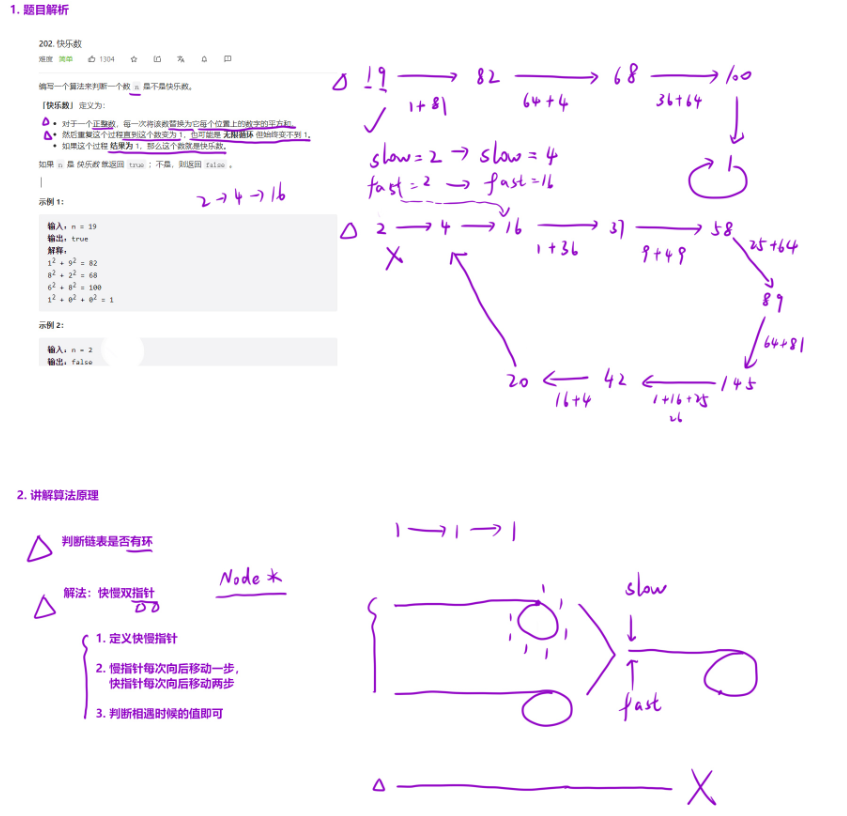
根据上述的题?分析，我们可以知道，当重复执? x 的时候，数据会陷?到?个「循环」之中。?「快慢指针」有?个特性，就是在?个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在?个位置上。如果相遇位置的值是 1 ，那么这个数?定是快乐数；如果相遇位置不是 1的话，那么就不是快乐数。

代码

class Solution {
    public boolean isHappy(int n) {
        // 快慢指针
        int slow = n;
        int fast = num(n);
        while(slow != fast) {
            slow = num(slow);
            fast = num(fast);
            fast = num(fast);
        }
        return slow == 1;
    }
    // 返回x这个数每一位上的平方
    private int num(int x) {
        int result = 0;
        while(x > 0) {
            result += (x % 10) * (x % 10);
            x /= 10;
        }
        return result;
    }
}

盛最多水的容器(mid)

题目链接：盛最多水的容器

算法思路

解法1：枚举遍历O(n^2),超时
解法2：对撞指针
设两个指针 left ，right 分别指向容器的左右两个端点，此时容器的容积 :
v = (right - left) * min( height[right], height[left])
容器的左边界为 height[left] ，右边界为 height[right] 。
为了?便叙述，我们假设「左边边界」?于「右边边界」。
如果此时我们固定?个边界，改变另?个边界，?的容积会有如下变化形式：

• 容器的宽度?定变?。
• 由于左边界较?，决定了?的?度。如果改变左边界，新的???度不确定，但是?定不会超过右边的柱??度，因此容器的容积可能会增?。
• 如果改变右边界，?论右边界移动到哪?，新的??的?度?定不会超过左边界，也就是不会超过现在的???度，但是由于容器的宽度减?，因此容器的容积?定会变?的。

由此可?，左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界，继续去判断下?个左右边界。
当我们不断重复上述过程，每次都可以舍去?量不必要的枚举过程，直到 left 与 right 相遇。期间产?的所有的容积??的最?值，就是最终答案。

代码

class Solution {
    public int maxArea(int[] height) {
        // 利用单调性，使用对撞指针来解决问题
        int left = 0;
        int right = height.length - 1;
        int max = 0;
        while(left < right) {
            if(height[left] < height[right]) {
                max = Math.max(max, (right - left) * height[left]);
                left++;
            }else {
                max = Math.max(max, (right - left) * height[right]);
                right--;
            }
        }
        return max;
    }
}

有效三角形的个数（mid)

题目链接：有效三角形个数

算法思路

代码

class Solution {
    public int triangleNumber(int[] nums) {
        // 1. 排序
        Arrays.sort(nums);
        // 2. 利用单调性，使用双指针
        // 先固定最大的数，在他的左区间使用双指针
        int count = 0;
        for(int i = nums.length - 1; i > 1; i--) {
            int left = 0;
            int right = i-1;
            while(left < right) {
                if(nums[left] + nums[right] > nums[i]) {
                    // left 到 right区间都是符合要求的可以直接跳过
                    count += right - left;
                    right--;
                }else {
                    left++;
                }
            }
        }
        return count;
    }
}

和为S的两个数（easy)

题目链接：和为S的两个数

算法思路：

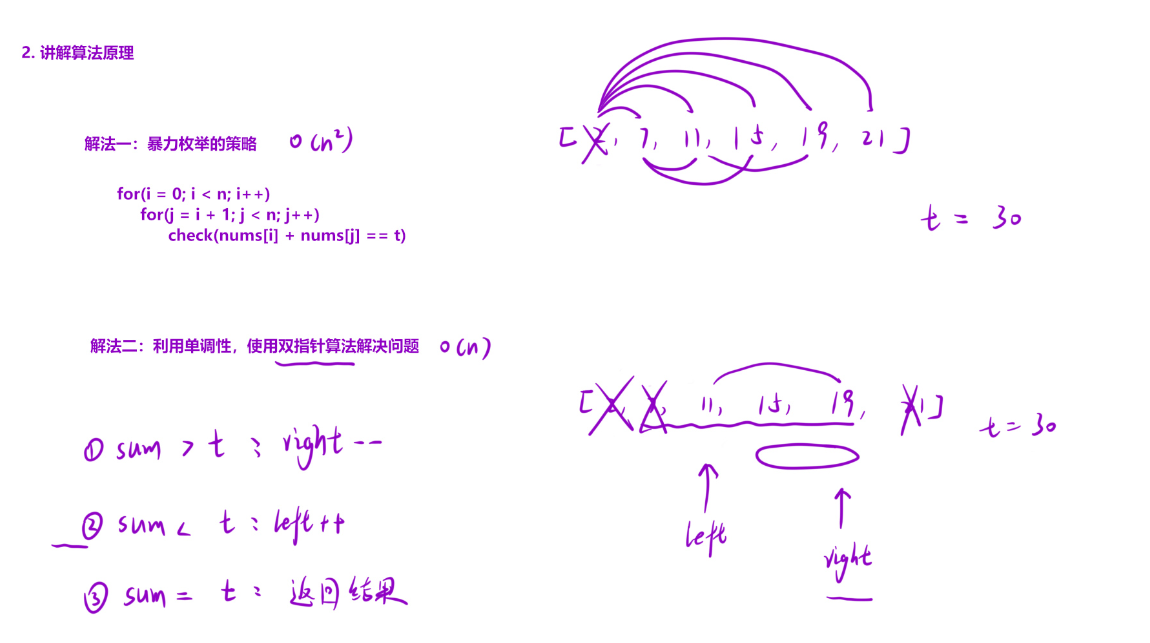
代码

class Solution {
    public int[] twoSum(int[] price, int target) {
        int left = 0;
        int right = price.length - 1;
        int[] result = new int[2];
        while(left < right) {
            if(price[left] + price[right] > target) {
                right--;
            }else if(price[left] + price[right] < target) {
                left++;
            }else {
                result[0] = price[left];
                result[1] = price[right];
                break;
            }
        }
        return result;
    }
}

三数之和（mid)

题目链接：三数之和

算法思路

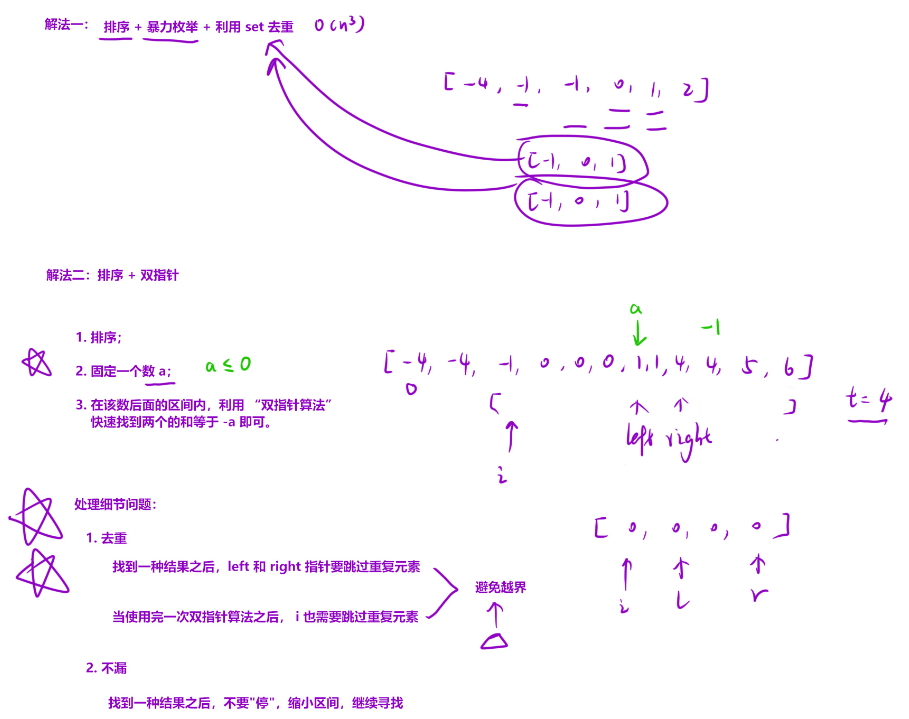
代码

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> result = new ArrayList<>();
        for(int i = nums.length - 1; i >= 2;) {
            int target = -nums[i];
            // 变成求两数之和为target
            int left = 0;
            int right = i - 1;
            while(left < right) {
                int sum = nums[left] + nums[right];
                if(sum < target) {
                    left++;
                }else if(sum > target) {
                    right--;
                }else {
                    result.add(new ArrayList<Integer>(Arrays.asList(nums[i], nums[left], nums[right])));
                    // 缩小空间，继续寻找
                    left++;
                    right--;
                    // 去重，如果有重复的就跳过
                    while(left < right && nums[left] == nums[left - 1]) left++;
                    while(left < right && nums[right] == nums[right + 1]) right--;
                }
            }            
            i--;
            // 去重
            while(i >= 2 &&  nums[i] == nums[i+1]) i--; 
        }
        return result;
    }
}

四数之和

题目链接：四数之和

算法思路

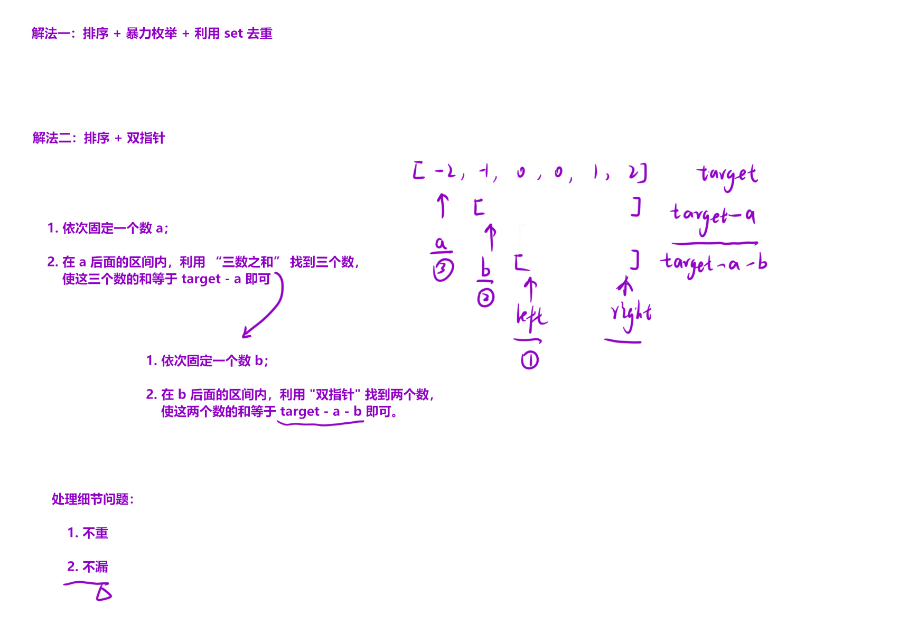
代码

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums);
        int n = nums.length;
        List<List<Integer>> result = new ArrayList<>();
        for(int i = 0; i < n - 3;) {
            // 三数之和
            for(int j = i+1; j < n - 2;) {
                // 大数处理
                long tmp = (long)target - nums[i] - nums[j];
                int left = j+1;
                int right = n - 1;
                while(left < right) {
                    int sum = nums[left] + nums[right];
                    if(sum > tmp) {
                        right--;
                    }else if(sum < tmp) {
                        left++;
                    }else {
                        result.add(new ArrayList<Integer>(Arrays.asList(nums[i], nums[j], nums[left], nums[right])));
                        left++;
                        right--;
                        while(left < right && nums[left] == nums[left - 1]) left++;
                        while(left < right && nums[right] == nums[right + 1]) right--;
                    }
                }
                j++;
                while(j < n - 2 && nums[j] == nums[j - 1]) j++;
            }
            i++;
            while(i < n - 3 && nums[i] == nums[i-1]) i++;
        }
        return result;
    }
}