day18 二叉树 part05

513. 找树左下角的值

中等
给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
层序遍历可以直接秒了，但是这里我们用递归的办法
请注意这里：回溯隐藏在这里！

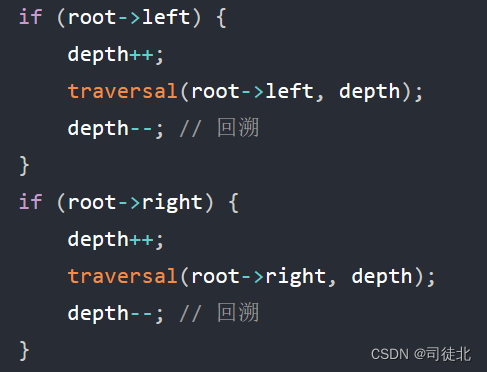
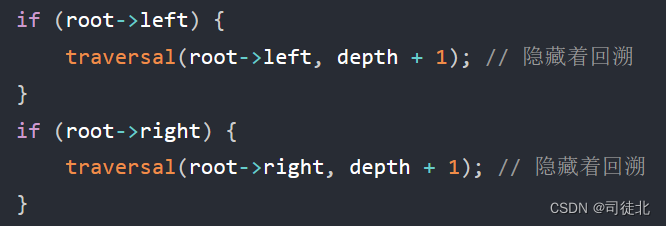
class Solution {
    private int Deep = 0; // 用于记录最大深度
    private int val = 0;  // 题目假设至少有一个节点，不用担心根节点为空，导致val结果就是初始化结果

    public int findBottomLeftValue(TreeNode root) {
        findLeftValue(root, 1);

        return val;
    }
    public void findLeftValue(TreeNode node, int deep) {
        if (node == null) {
            return; // 如果节点为空自然是对val和Deep不做任何处理
        }
        if (Deep < deep) { // 如果此时最大深度小于当前深度，如果最大深度大于等于当前深度了，那就说明以前已经有一样深或更深的左节点（因为我们是先递归左节点，再递归右节点，怎么也不可能先找着右节点，除非深度更深）被访问过了，就不用记录当前节点了
            Deep++; // 更新深度
            val = node.val; //说明val值还不是最底层的值，需要更新一下
        }
        findLeftValue(node.left, deep + 1); // 隐藏着回溯
        findLeftValue(node.right, deep + 1); // 隐藏着回溯
        
    }
}

112. 路径总和

简单
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
叶子节点 是指没有子节点的节点。
这题我一下就做出来了……虽然我有的地方还没有特别想通，但我感觉都是一个套路，一写就秒了

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return traversal(root, targetSum);
    }
    public boolean traversal(TreeNode node, int targetSum){
        if (node == null) {
            return false;
        }
        if (node.left == null && node.right == null){ // 如果当前节点是叶子节点，就判断它满不满足目标和
            if (node.val == targetSum){
                return true;
            }
        }
        boolean leftBool = traversal(node.left, targetSum - node.val);  //隐藏着回溯
        boolean rightBool = traversal(node.right, targetSum - node.val); //隐藏着回溯

        return leftBool || rightBool; //这里不是&&，因为是在左右两条路里找到一条合格的就行
    }
}

113. 路径总和 II

中等
给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<>(); //存放最终结果
        List<Integer> path = new ArrayList<>(); // 存放单独一条路径

        traversal(root, targetSum, res, path);

        return res;
    }
    public void traversal(TreeNode node, int targetSum, List<List<Integer>> res, List<Integer> path) {
        if (node == null) {
            return; // 如果这个节点是空的，那肯定不能把它添加进路径
        }

        if (node.left == null && node.right == null) { // 是否为叶子节点
            if(node.val == targetSum){
                path.add(node.val);
                res.add(new ArrayList<>(path)); // res.add(path);不能这么写！！！
                path.remove(path.size() - 1);
            }
            return; // 叶子节点下面肯定是空，没有必要继续遍历后面了
        }
        path.add(node.val);
        traversal(node.left, targetSum - node.val, res, path);
        path.remove(path.size() - 1);
        
        path.add(node.val);
        traversal(node.right, targetSum - node.val, res, path);
        path.remove(path.size() - 1);
    }
}

106. 从中序与后序遍历序列构造二叉树

中等
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

难点：根节点的左右子树在无论前序，中序，后序都是会以某个元素为界限分开的，而不会说，交叉着来，归根到底是因为，无论中左右，左中右，左右中，都是左在先，右在后，在没有把左子树遍历完之前，是不会访问右子树的

难点：这个题不是让你真的输出这种 [3,9,20,null,null,15,7]，而是你返回一个root节点，root是二叉树的根节点就行。

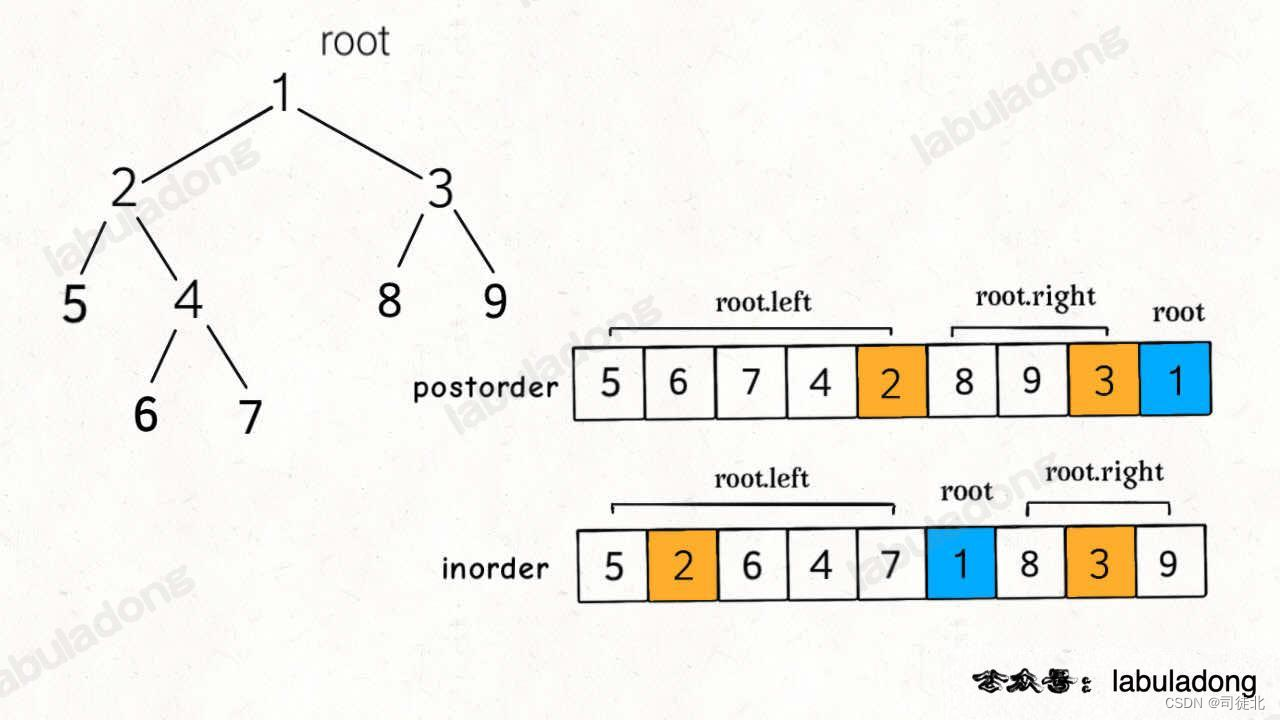
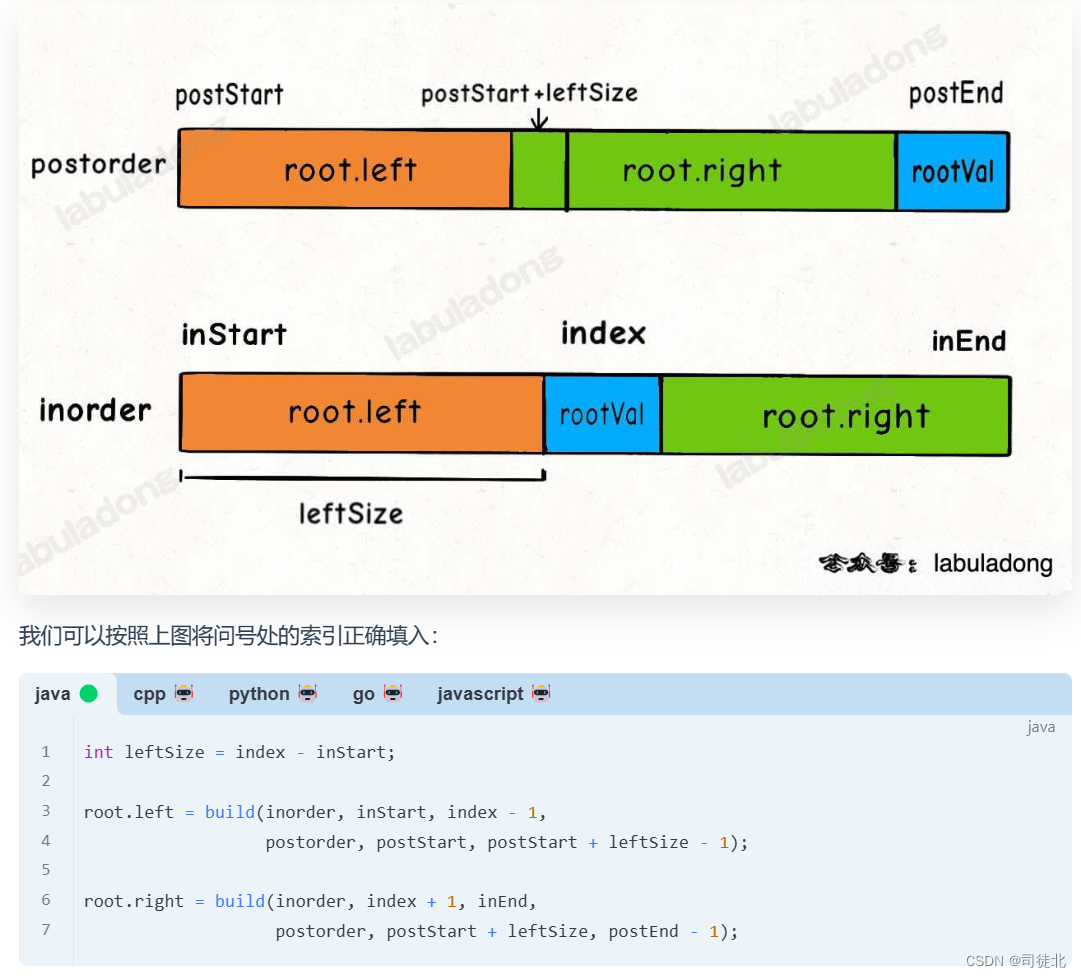
class Solution {
    HashMap<Integer, Integer> valToIndex = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < postorder.length; i++){
            valToIndex.put(inorder[i], i); // 这里是建立中序的索引，不是后序的，因为中序可以将遍历数组分成两半
        }
        // inorder.length - 1 代表的是最后一个元素的索引，所以要 - 1
        return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
    }
    /* 
    build 函数的定义：
    后序遍历数组为 postorder[postStart..postEnd]，
    中序遍历数组为 inorder[inStart..inEnd]，
    构造二叉树，返回该二叉树的根节点 
*/
    public TreeNode build(int[] inorder, int inStart, int inEnd, 
                        int[] postorder, int postStart, int postEnd){
        if (inStart > inEnd) return null; // 最多就是inStart 等于InEnd（当中序遍历数组只有一个元素时）
        int rootVal = postorder[postEnd]; // root节点对应的值就是后序遍历数组的最后一个元素
        int rootIndex = valToIndex.get(rootVal); // rootVal 在中序遍历数组中的索引
        TreeNode root = new TreeNode(rootVal);
        int leftSize = rootIndex - inStart;

        root.left = build(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);
        root.right = build(inorder, rootIndex + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);

        return root;
    }
}

105. 从前序与中序遍历序列构造二叉树

中等
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

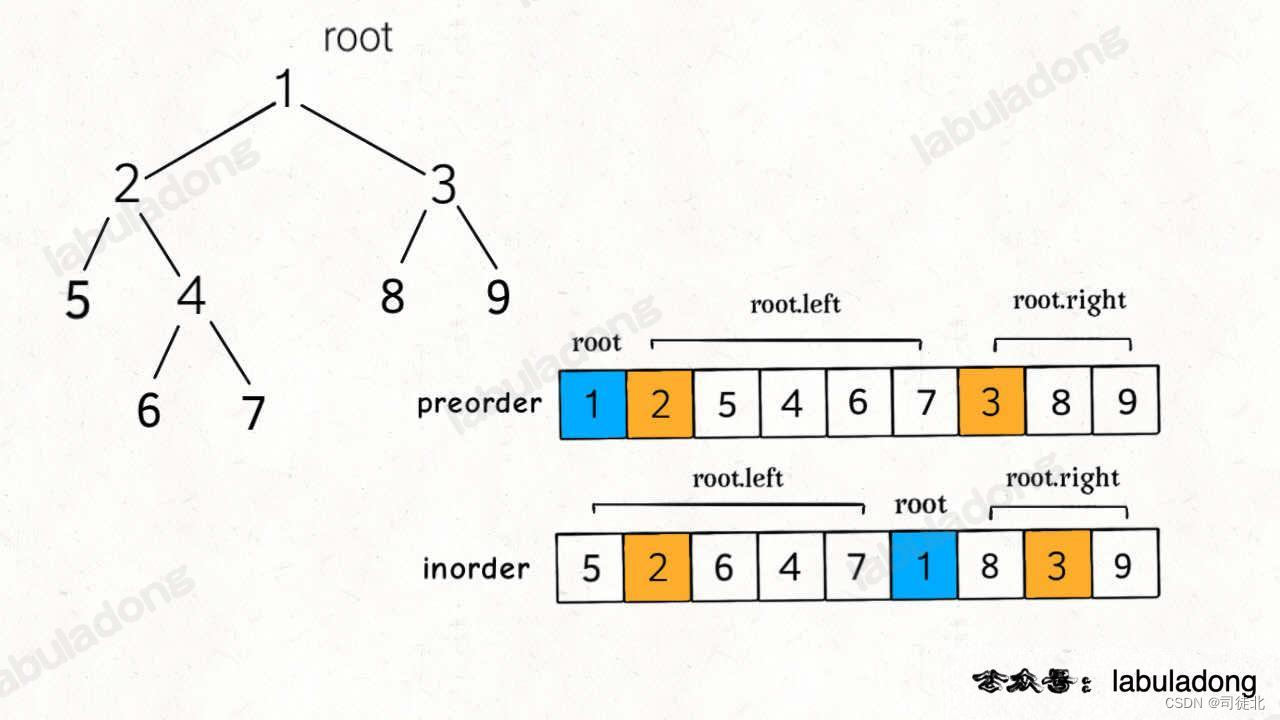
class Solution {
    HashMap<Integer, Integer> valToIndex = new HashMap<>(); // 存放中序（别忘了写new）

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++){
            valToIndex.put(inorder[i], i);
        }

        return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }
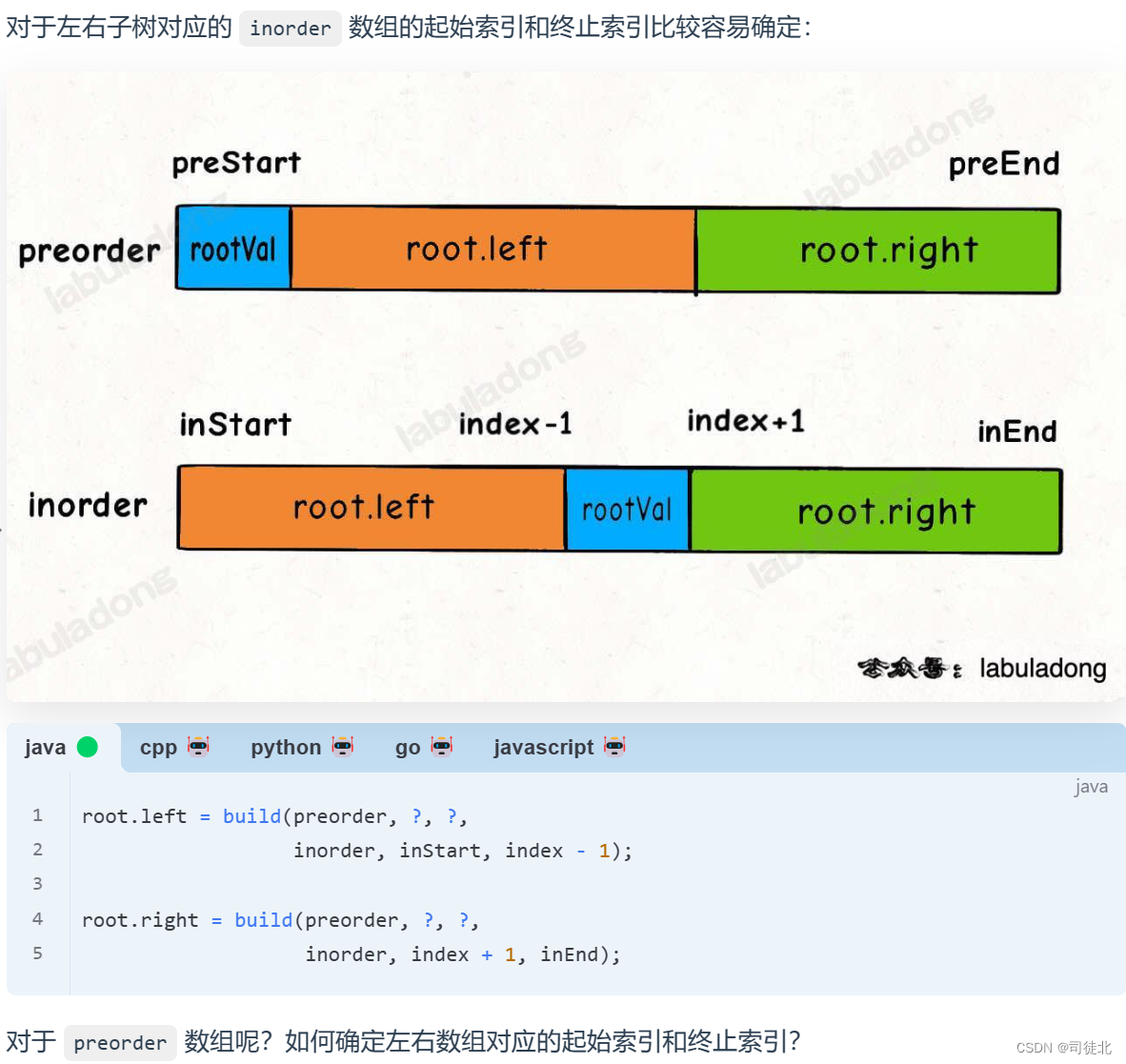
    public TreeNode build(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
        if (inStart > inEnd) return null;

        int rootVal = preorder[preStart];
        int rootIndex = valToIndex.get(rootVal);
        int leftSize = rootIndex - inStart;

        TreeNode root = new TreeNode(rootVal);
        root.left = build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, rootIndex - 1);
        root.right = build(preorder, preStart + leftSize + 1, preEnd, inorder, rootIndex + 1, inEnd);

        return root;
    }
}