基于PID神经网络的系统控制(附带Matlab代码)
基于PID神经网络的系统控制(附带Matlab代码)
1. PID神经元网络结构
PID神经元网络从结构上可以分为输入层、隐含层和输出层三层,n 个控制量的 PID神经元网络包含 n个并列的相同子网络,各子网络间既相互独立,又通过网络连接权值相互联系每个子网络的输入层有两个神经元,分别接收控制量的目标值和当前值。每个子网络的隐含层由比例元积分元和微分元构成,分别对应着 PID 控制器中的比例控制积分控制和微分控制。PID神经元网络按被控系统控制量的个数可以分为控制单变量系统的单控制量神经元网络和控制多变量系统的多控制量神经元网络。其中单控制量神经元网络是 PID神经元网络的基本形式,多控制量神经元网络可以看成是多个单控制量神经元网络的组合形式。
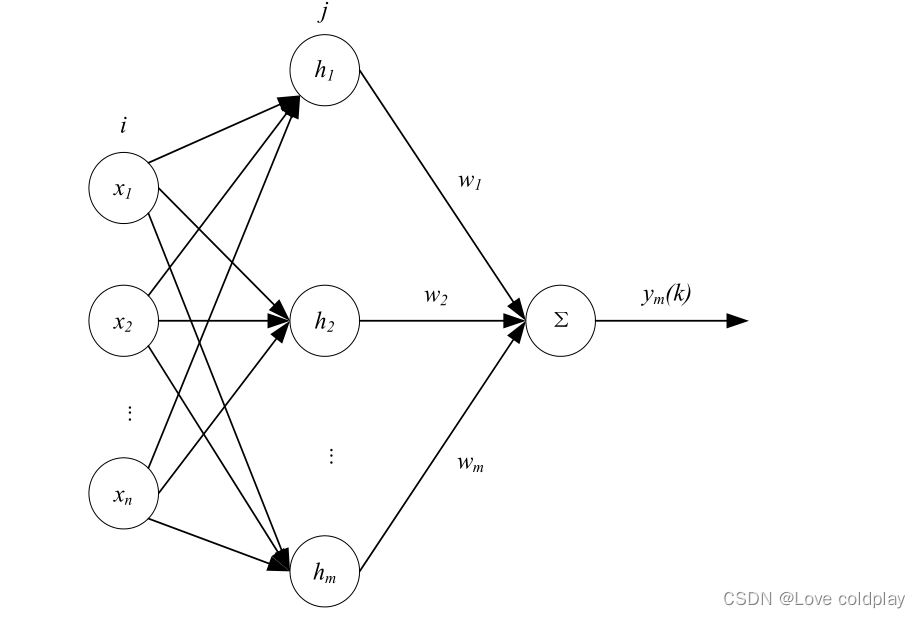
图中,X1是控制量的控制目标,X2是控制量当前值,Y是神经元网络计算得到的控制律,wij和wjk是网络权值,从中可以看到单控制量神经元网络是一个三层前向神经元网络,网络结构为2一3一1,隐含层包含比例元积分元和微分元三个神经元。多控制量神经元网络可以看成多个单控制量网络的并联连接,多控制量神经元网络拓扑结构如下图所示。
图中,X11,X21,…,Xn1是控制量的控制目标;X12,X22,…,Xn2是控制量的当前值;Y1,Y2,···,Yn是多控制量神经元网络计算得到的控制律;wij和wjk是网络权值。
2. 控制律计算
PID 神经元网络分为输入层、隐含层和输出层,网络输入量为控制量当前值和控制目标,输出量为控制律,各层输人输出计算公式如下。
(1)输入层
输人层中包含2n个神经元,输出数据xsi等于输人数据Xsi计算公式为
(2)隐含层
隐含层有 3n个神经元,包括n个比例神经元个积分神经元和个微分神经元这些神经元的输人值相同,计算公式为
(3)输出层
输出层有n个神经元构成n 维输出量输出层的输出为隐含层全部神经元的输出值加权和,计算公式如下:
图片
3. 权值修正
PID神经元网络在控制的过程中根据控制量误差按照梯度修正法修正权值,使得控制量不断接近控制目标值,权值修正的过程如下。
4.结果展示
clc
clear
close all
%% 网络结构初始化
rate1=0.006;rate2=0.001; %学习率
k=0.3;K=3;
y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值
u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率
h1i=zeros(3,1);h1i_1=h1i; %第一个控制量
h2i=zeros(3,1);h2i_1=h2i; %第二个控制量
h3i=zeros(3,1);h3i_1=h3i; %第三个空置量
x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出
%权值初始化
k0=0.03;
%第一层权值
w11=k0*rand(3,2);
w12=k0*rand(3,2);
w13=k0*rand(3,2);
%第二层权值
w21=k0*rand(1,9);
w22=k0*rand(1,9);
w23=k0*rand(1,9);
%值限定
ynmax=1;ynmin=-1; %系统输出值限定
xpmax=1;xpmin=-1; %P节点输出限定
qimax=1;qimin=-1; %I节点输出限定
qdmax=1;qdmin=-1; %D节点输出限定
uhmax=1;uhmin=-1; %输出结果限定
%% 网络迭代优化
for k=1:1:200
%% 控制量输出计算
%--------------------------------网络前向计算--------------------------
%系统输出
y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);
y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);
y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);
r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标
%系统输出限制
yn=[y1(k),y2(k),y3(k)];
yn(find(yn>ynmax))=ynmax;
yn(find(yn<ynmin))=ynmin;
%输入层输出
x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];
%隐含层
x1i=w11*x1o;
x2i=w12*x2o;
x3i=w13*x3o;
%比例神经元P计算
xp=[x1i(1),x2i(1),x3i(1)];
xp(find(xp>xpmax))=xpmax;
xp(find(xp<xpmin))=xpmin;
qp=xp;
h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);
%积分神经元I计算
xi=[x1i(2),x2i(2),x3i(2)];
qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];
qi=qi_1+xi;
qi(find(qi>qimax))=qimax;
qi(find(qi<qimin))=qimin;
h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);
%微分神经元D计算
xd=[x1i(3),x2i(3),x3i(3)];
qd=[0 0 0];
xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];
qd=xd-xd_1;
qd(find(qd>qdmax))=qdmax;
qd(find(qd<qdmin))=qdmin;
h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);
%输出层计算
wo=[w21;w22;w23];
qo=[h1i',h2i',h3i'];qo=qo';
uh=wo*qo;
uh(find(uh>uhmax))=uhmax;
uh(find(uh<uhmin))=uhmin;
u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律



本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!