机器学习数据处理

欢迎关注博主 Mindtechnist 或加入【Linux C/C++/Python社区】一起学习和分享Linux、C、C++、Python、Matlab，机器人运动控制、多机器人协作，智能优化算法，滤波估计、多传感器信息融合，机器学习，人工智能等相关领域的知识和技术。

---

NumPy

• • 什么是NumPy
  • ndarray对象
  • 安装NumPy
  • NumPy基本操作
  • NumPy运算操作
  • NumPy矩阵操作
  • 图书推荐

---

专栏：《机器学习》

---

什么是NumPy

NumPy 是 Numerical Python 的缩写，它是一个由多维数组对象（ndarray）和处理这些数组的函数（function）集合组成的库。使用 NumPy 库，可以对数组执行数学运算和相关逻辑运算。NumPy 不仅作为 Python 的扩展包，它同样也是 Python 科学计算的基础包。NumPy 提供了大量的数学函数，主要用来计算、处理一维或多维数组，支持常见的数组和矩阵操作。NumPy 的底层主要用 C语言编写，因此它能够高速地执行数值计算。NumPy 还提供了多种数据结构，这些数据结构能够非常契合的应用在数组和矩阵的运算上。

NumPy 作为一个开源项目，它由许多协作者共同开发维护，随着数据科学（Data Science，简称 DS，包括大数据分析与处理、大数据存储、数据抓取等分支）的蓬勃发展，像 NumPy、SciPy（Python科学计算库）、Pandas（基于NumPy的数据处理库） 等数据分析库都有了大量的增长，它们都具有较简单的语法格式。NumPy 通常会和Matplotlib等搭配一块使用。

NumPy主要有以下优势
①ndarray支持并行化运算（向量化运算）
numpy内置了并行运算功能，当系统有多个核心时，做某种计算时，numpy会自动做并行计算。
②效率远高于纯Python代码
Numpy底层使用C语言编写，内部解除了GIL（全局解释器锁），其对数组的操作速度不受Python解释器的限制，所以，其效率远高于纯Python代码。
③ndarray在存储数据的时候，数据与数据的地址都是连续的，这样就使得批量操作数组元素时速度更快。

ndarray中的所有元素的类型都是相同的，而Python列表中的元素类型是任意的，所以ndarray在存储元素时内存可以连续，而python原生list就只能通过寻址方式找到下一个元素，这虽然也导致了在通用性能方面Numpy的ndarray不及Python原生list，但在科学计算中，Numpy的ndarray就可以省掉很多循环语句，代码使用方面比Python原生list简单的多。

ndarray对象

NumPy 定义了一个 n 维数组对象，简称 ndarray 对象，它是一个一系列相同类型元素组成的数组集合。数组中的每个元素都占有大小相同的内存块，使用索引或切片的方式可以获取数组中的每个元素。ndarray 对象有一个 dtype 属性，该属性用来描述元素的数据类型。ndarray 对象采用了数组的索引机制，将数组中的每个元素映射到内存块上，并且按照一定的布局对内存块进行排列，常用的布局方式有两种，即按行或者按列。

创建ndarray对象
通过 NumPy 的内置函数 array() 可以创建 ndarray 对象，其语法格式如下：

numpy.array(object, dtype = None, copy = True, order = None,ndmin = 0)

使用NumPy创建数组

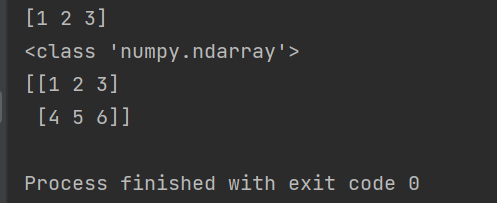
import numpy as np

a = np.array([1,2,3])
b = np.array([[1,2,3], [4,5,6]])

print(a)
print(type(a))

print(b)

运行结果如下

查看数组维数并变维

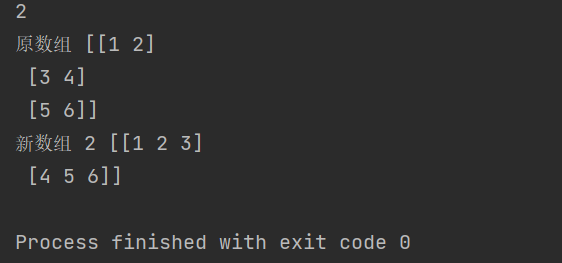
import numpy as np

a = np.array([[1,2], [3,4], [5,6]])

print(a.ndim)
print("原数组", a)

a = a.reshape(2,3)
print("新数组", a.ndim, a)

运行结果如下

ndarray的属性
ndarray的属性如下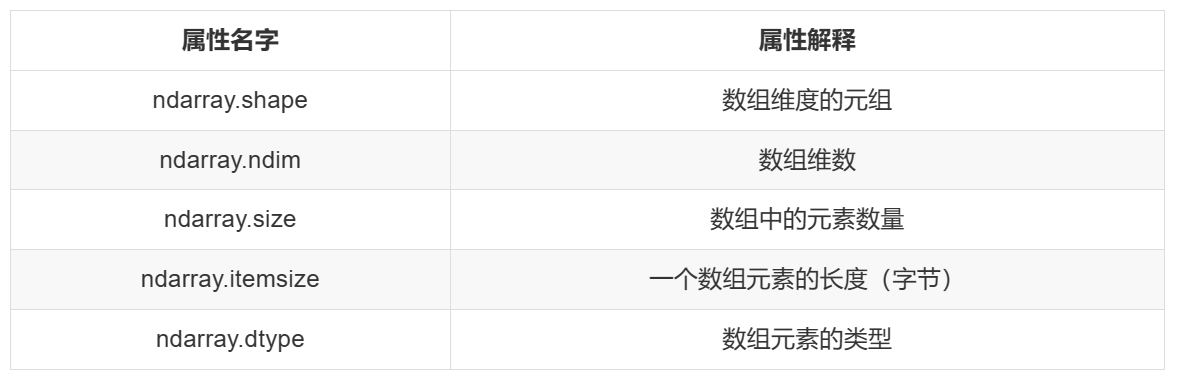
通过ndarray的属性也可以操作数组

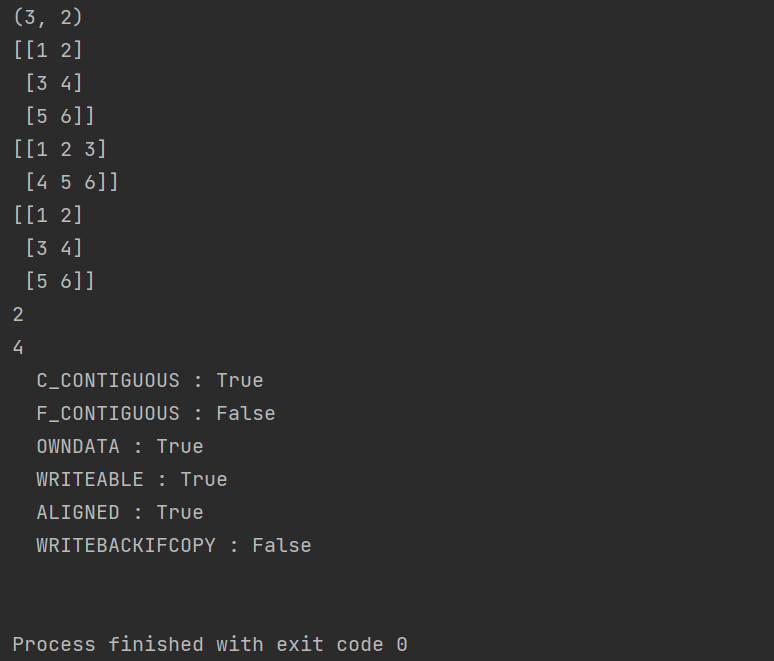
import numpy as np

a = np.array([[1,2], [3,4], [5,6]])

#输出a的维度
print(a.shape)
print(a)

#改变a的维度
a.shape = (2, 3)
print(a)

#通过函数改变a的维度
print(a.reshape(3, 2))

#打印数组维数
print(a.ndim)

#以字节为单位输出数组中每个元素的大小
print(a.itemsize)

#输出数组的内存信息
print(a.flags)

打印结果如下

ndarray的类型
ndarray的类型包括

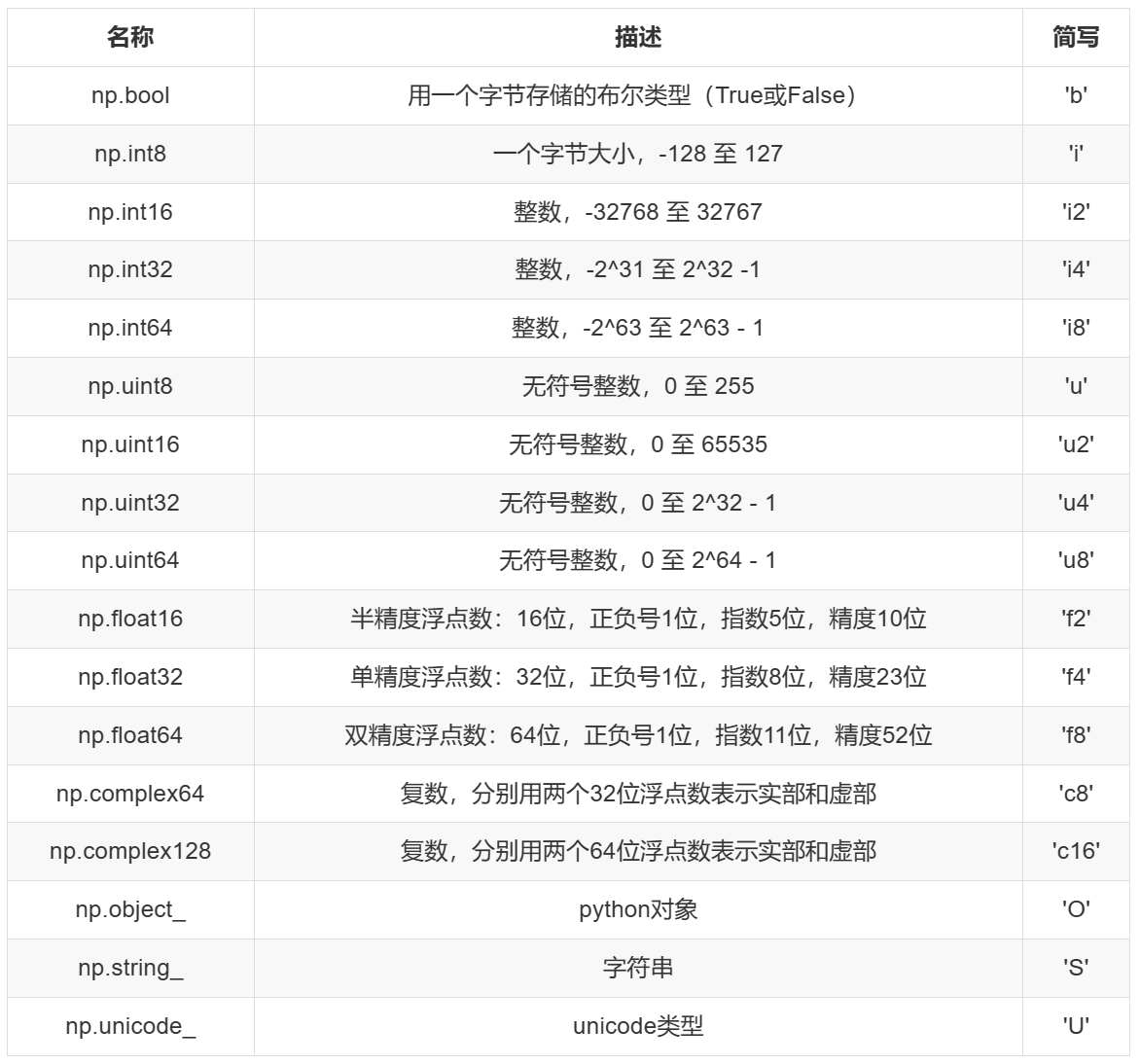
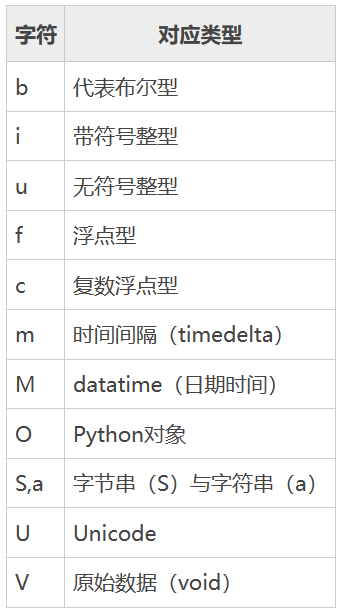
NumPy中的数据类型标识码，NumPy 中每种数据类型都有一个唯一标识的字符码，如下所示：

安装NumPy

Windows安装NumPy
最简单的方式是通过包管理器pip命令安装

pip install numpy  

通常，NumPy 与 SciPy 程序包一起使用，SciPy 可以看做对 NumPy 库的扩展，它在 NumPy 的基础上又增加了许多工程计算函数。（此处暂且只讲解安装NumPy）

Linux安装NumPy
本人使用的Linux版本为CentOS，运行如下命令即可

$ sudo yum install numpy scipy python-matplotlib ipython python-pandas sympy python-nose

NumPy基本操作

numpy.empty()
numpy.empty() 创建未初始化的数组，可以指定创建数组的形状（shape）和数据类型（dtype）。

numpy.empty(shape, dtype = float, order = 'C')

参数：

• shape：指定数组的形状；
• dtype：数组元素的数据类型，默认值是值 float；
• order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

numpy.zeros()
该函数用来创建元素均为 0 的数组，同时还可以指定被数组的形状。

numpy. zeros(shape,dtype=float,order="C")

参数：

• shape：指定数组的形状；
• dtype：数组元素的数据类型，默认值是值 float；
• order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

numpy.ones()
返回指定形状大小与数据类型的新数组，并且新数组中每项元素均用 1 填充。

numpy.ones(shape, dtype = None, order = 'C')

numpy.asarray()
asarray() 能够将一个 Python 序列转化为 ndarray 对象。

numpy.asarray（sequence，dtype = None ，order = None ）

参数：

• sequence：接受一个 Python 序列，可以是列表或者元组；
• dtype：可选参数，数组的数据类型，默认值是值 float；
• order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”（“C”代表以行顺序存储，“F”则表示以列顺序存储）。

numpy.frombuffer()
表示使用指定的缓冲区创建数组。

numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)

参数：

• buffer：将任意对象转换为流的形式读入缓冲区；
• dtype：返回数组的数据类型，默认是 float32；
• count：要读取的数据数量，默认为 -1 表示读取所有数据；
• offset：读取数据的起始位置，默认为 0。

numpy.fromiter()
把迭代对象转换为 ndarray 数组，其返回值是一个一维数组。

numpy.fromiter(iterable, dtype, count = -1)

参数：

• iterable：可迭代对象；
• dtype：数组元素的数据类型，默认值是值 float；
• count：读取的数据数量，默认为 -1，读取所有数据。

numpy.arange()
创建给定数值范围的数组。

numpy.arange(start, stop, step, dtype)

参数：

• start： 起始值，默认是 0。
• stop： 终止值，注意生成的数组元素值不包含终止值。
• step： 步长，默认为 1。
• dtype： 可选参数，指定 ndarray 数组的数据类型。

numpy.linspace()
表示在指定的数值区间内，返回均匀间隔的一维等差数组，默认均分 50 份。

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数：

• start：代表数值区间的起始值；
• stop：代表数值区间的终止值；
• num：表示数值区间内要生成多少个均匀的样本。默认值为 50；
• endpoint：默认为 True，表示数列包含 stop 终止值，反之不包含；
• retstep：默认为 True，表示生成的数组中会显示公差项，反之不显示；
• dtype：代表数组元素值的数据类型。

numpy.logspace()
创建等比数组，返回一个 ndarray 数组。

numpy.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

参数：

• start： 序列的起始值：base**start。
• stop： 序列的终止值：base**stop。
• num： 数值范围区间内样本数量，默认为 50。
• endpoint： 默认为 True 包含终止值，反之不包含。
• base： 对数函数的 log 底数，默认为10。
• dtype： 可选参数，指定 ndarray 数组的数据类型。

NumPy运算操作

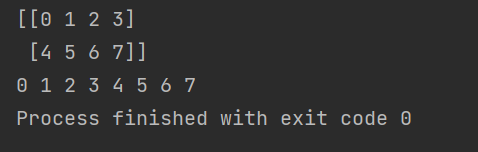
numpy.ndarray.flat()
numpy.ndarray.flat() 返回一个数组迭代器，可以用 for 循环遍历其中的每一个元素。

import numpy as np

a = np.arange(8).reshape(2, 4)

print (a)

for e in a.flat:
    print (e, end=" ")

numpy.ndarray.flatten()
以一维数组的形式返回一份数组副本，对副本修改不会影响原始数组。

import numpy as np

a = np.arange(8).reshape(2, 4)

print (a)
print(a.flatten())

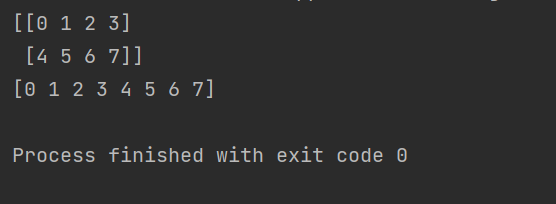
numpy.ravel()
返回一个连续的扁平数组（即展开的一维数组），与 flatten不同，它返回的是数组视图（修改视图会影响原数组）。

NumPy 的位运算

算术运算
NumPy 数组的“加减乘除”算术运算，分别对应 add()、subtract()、multiple() 以及 divide() 函数。
numpy.reciprocal()函数对数组中的每个元素取倒数，并以数组的形式将它们返回。
numpy.power()将 a 数组中的元素作为底数，把 b 数组中与 a 相对应的元素作幂 ，最后以数组形式返回两者的计算结果。
numpy.mod()返回两个数组相对应位置上元素相除后的余数

NumPy矩阵操作

Matrix矩阵库
NumPy 提供了一个 矩阵库模块numpy.matlib，该模块中的函数返回的是一个 matrix 对象，而非 ndarray 对象。矩阵由 m 行 n 列（m*n）元素排列而成，矩阵中的元素可以是数字、符号或数学公式等。
matlib.empty() 返回一个空矩阵，它的创建速度非常快。
numpy.matlib.zeros() 创建一个以 0 填充的矩阵。
numpy.matlib.ones() 创建一个以 1 填充的矩阵。
numpy.matlib.eye() 返回一个对角线元素为 1，而其他元素为 0 的矩阵 。
numpy.matlib.identity()该函数返回一个给定大小的单位矩阵，矩阵的对角线元素为 1，而其他元素均为 0。
numpy.matlib.rand() 创建一个以随机数填充，并给定维度的矩阵。

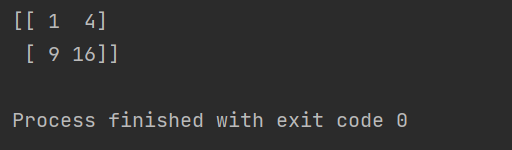
multiple()
函数用于两个矩阵的逐元素乘法。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)

a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.multiply(a1, a2))

matmul()
用于计算两个数组的矩阵乘积。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)

a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.matmul(a1, a2))

dot()
函数用于计算两个矩阵的点积。

import numpy as np

a1=np.array([[1,2], [3,4]], ndmin=2)

a2=np.array([[1,2], [3,4]], ndmin=2)

print(np.dot(a1, a2))

numpy.inner()
用于计算数组之间的内积。
numpy.linalg.solve()
该函数用于求解线性矩阵方程组，并以矩阵的形式表示线性方程的解。
numpy.linalg.inv()
该函数用于计算矩阵的逆矩阵，逆矩阵与原矩阵相乘得到单位矩阵。

图书推荐

🔥通用人工智能：初心与未来

自20世纪50年代图灵在其划时代论文《计算机器与智能》中提出“图灵测试”以及之后的达特茅斯研讨会开始，用机器来模仿人类学习及其他方面的智能，即实现“人工智能”（Artificial Intelligence，AI）便成为计算机领域持续的研究热点。达特茅斯会议指出，“人工智能”的研究目标是实现能模拟人类的机器，该机器能使用语言，具有概念抽象和理解能力，能够完成人类才能完成的任务并能不断提高自身能力。当时的主要“智能”议题包括自动计算机、自然语言处理、神经网络、计算理论、自我改造、抽象、随机性和创造性等方面。这可以说是人工智能发展的“初心”，也是一项雄心勃勃的科学目标。
“人工智能”概念被提出后，在过去60多年里得到了广泛关注并迅速成长为学科前沿，进而沿着“从符号主义走向连接主义”和“从逻辑走向知识”两个方向蓬勃发展。时至今日，以深度学习为代表的新一波人工智能正在兴起。自然语言处理、人脸识别、自动驾驶、无人系统等复杂人工智能任务相继取得大的突破，人工智能在很多特定问题（如围棋、《星际争霸》游戏、医疗诊断等）的解决上甚至超过了人类的水平。这也引起了新的担忧，有些人认为人工智能将很快取代人类，人类的发展在不远的将来会面临极大挑战（机器人世界末日将会到来）。
下面推荐一本书，该书尝试给人们一个新的视角，即尽管人工智能已经变得越来越复杂而强大，但计算机科学还远未创造出通用人工智能（General AI）。作者结合人类自然智能的认知机理以及人工智能发展的初心与使命，带我们从不同方面细致分析了当前人工智能技术的不足，以及从当前“专用人工智能”到实现真正的“通用人工智能”还需要在哪些方面取得突破。书中对当前人工智能技术的发展路径提出了不少质疑，也给出了新的发展导向，如“通用智能不是算法优化”“自然智能会抄捷径”“通用智能需要富有洞察力的思考”“机器创造力需要创新的表示能力”“从少量例子中学习的能力”“全脑仿真智能”等，这将为通用人工智能的演化路径带来新的思考和借鉴。

书名：《通用人工智能：初心与未来》
作者：赫伯特·L.罗埃布莱特（Herbert L. Roitblat）
译者：郭斌
出版社：机械工业出版社
内容简介：至少从 20 世纪 50 年代起，人们就开始大肆宣传可能很快就会创造出一种能够与人类智能的全部范围和水平相匹配的机器。现在，我们已经成功地创造出了能够解决特定问题的机器，其准确度达到甚至超过了人类，但我们仍然无法获得通用智能。这本书想和大家探讨一下还需要做什么样的努力才能不仅获得专用智能，还能获得通用智能。如果读者对智能感兴趣，想了解更多关于如何建造自主机器的知识，或者担心这些机器突然有一天会以一种被称为“技术奇点”的方式统治世界，请阅读本书。
通过阅读本书，读者将会了解到：

• 尽管人工智能已经变得越来越复杂而强大，但计算机科学还远未创造出通用人工智能 。
  人类自然智能的认知机理以及人工智能发展的初心与使命，从不同方面认知当前人工智能技术的不足。
• 从当前“专用人工智能”到实现真正的“通用人工智能”还需要在哪些方面取得突破。
• 机器智能的进步可能会改变人们从事的工作类型，但它们不会意味着人类存在的终结。
• 为什么机器智能的改进并不会导致由机器所主导的失控性革命，机器智能的进步并不会导致世界末日的到来。

---

---