代码随想录刷题题Day18

刷题的第十八天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day18 任务
● 235. 二叉搜索树的最近公共祖先
● 701.二叉搜索树中的插入操作
● 450.删除二叉搜索树中的节点

1 二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

思路：
因为是有序树，所以如果中间节点是q,p的公共祖先，那么中间节点一定是在[p,q]区间的。

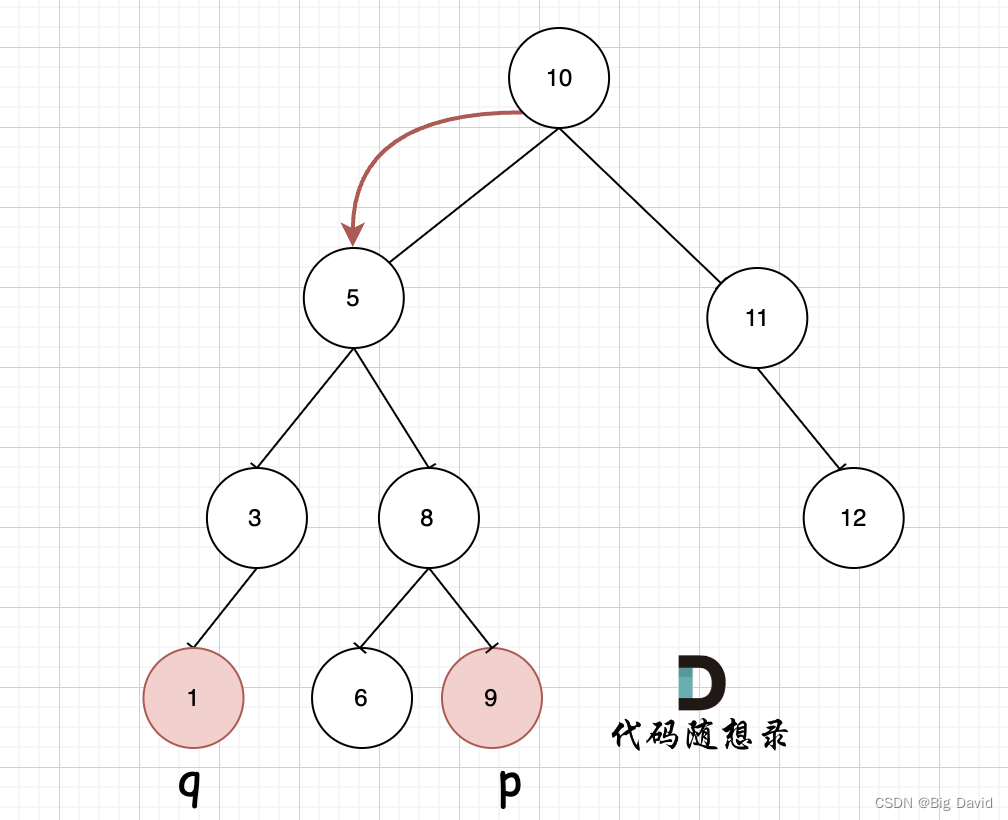
节点5是不是最近公共祖先？
如果从节点5继续向左遍历，那么将错过成为p的祖先， 如果从节点5继续向右遍历则错过成为q的祖先。
所以当从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。

递归法
（1）确定递归函数返回值以及参数

参数：当前节点，和两个节点p,q
返回值：TreeNode *

TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q)

（2）确定终止条件

遇到空返回

if (root == NULL) return root;

其实不需要这个终止条件，p、q 为不同节点且均存在于给定的二叉搜索树中，也就是说一定会找到公共祖先的，所以并不存在遇到空的情况

（3）确定单层递归的逻辑
寻找区间[p->val, q->val]

1. 那么如果 root->val 大于 p->val，同时 root->val 大于q->val，那么就应该向左遍历（说明目标区间在左子树上）
2. 如果 root->val 小于 p->val，同时 root->val 小于 q->val，那么就应该向右遍历（目标区间在右子树）
3. 剩下就是cur节点在区间（p->val <= root->val && root->val <= q->val）或者 （root->val <= cur->val &&root->val <= p->val）中，那么root就是最近公共祖先了，直接返回root

if (root->val > p->val && root->val > q->val) {
	TreeNode* left = traversal(root->left, p, q);
	if (left != NULL) return left;
}
else if (root->val < p->val && root->val < q->val) {
	TreeNode* right = traversal(root->right, p, q);
	if (right != NULL) return right;
}
else return root;

C++：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == NULL) return root;
        if (root->val > p->val && root->val > q->val) {// 左
            TreeNode* left = lowestCommonAncestor(root->left, p, q);
            return left;
        }
        else if (root->val < p->val && root->val < q->val) {// 右
            TreeNode* right = lowestCommonAncestor(root->right, p, q);
            return right;
        }
        else return root;
    }
};

精简C++：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        } else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        } else return root;
    }
};

迭代法
利用二叉搜索树的有序性

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while (root) {
            if (root->val > p->val && root->val > q->val) {
                root = root->left;
            }
            else if (root->val < p->val && root->val < q->val) {
                root = root->right;
            }
            else return root;
        }
        return NULL;
    }
};

---

2 二叉搜索树中的插入操作

701.二叉搜索树中的插入操作


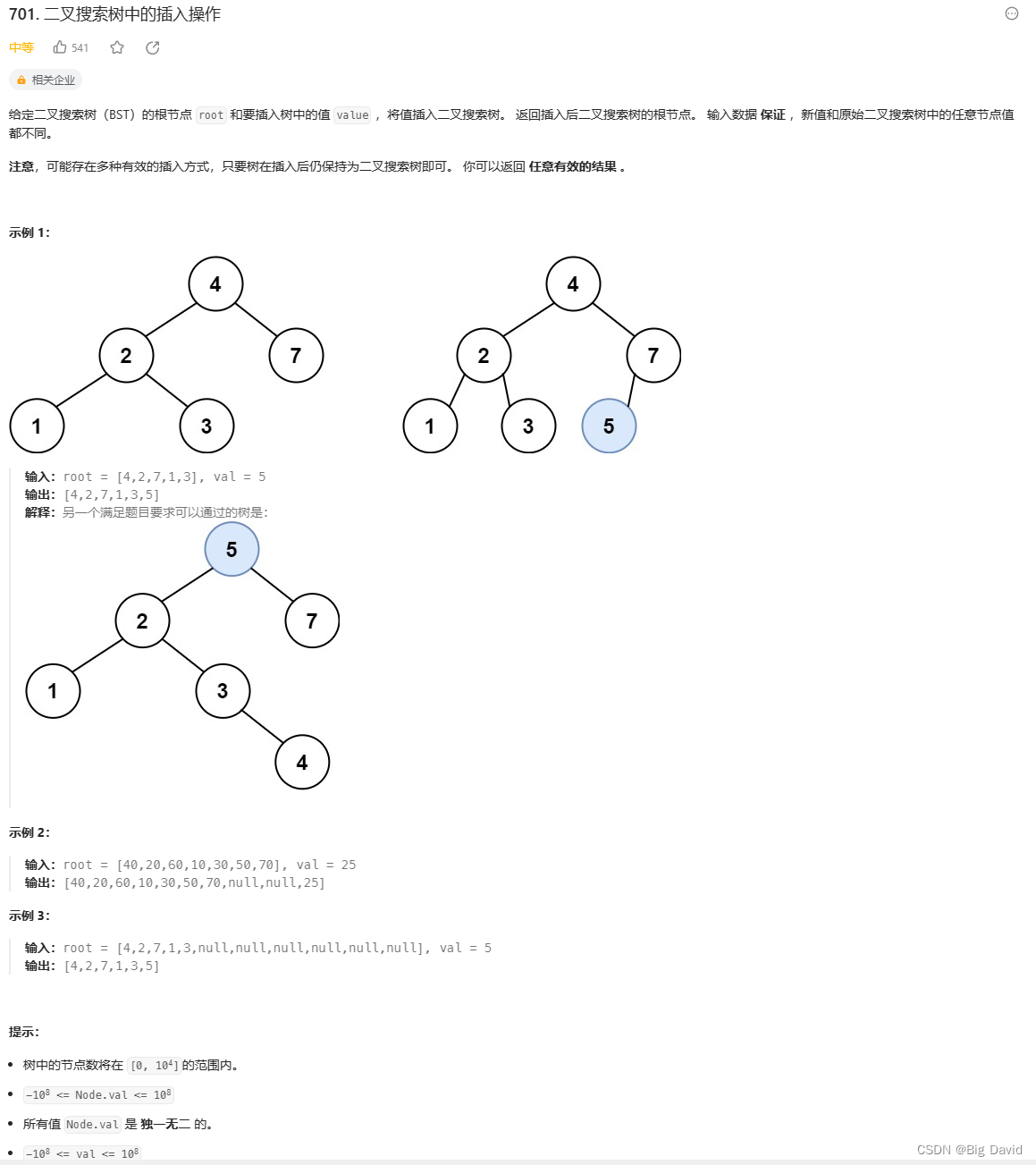
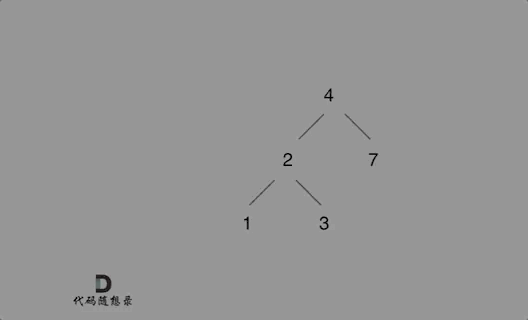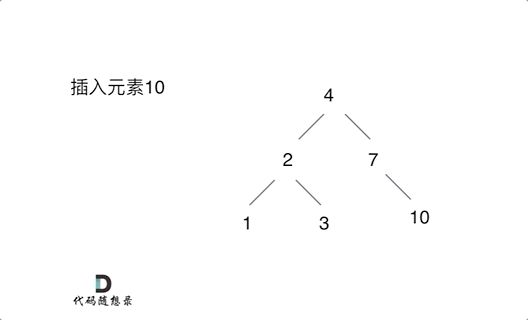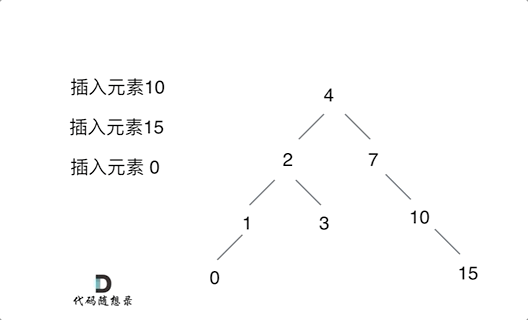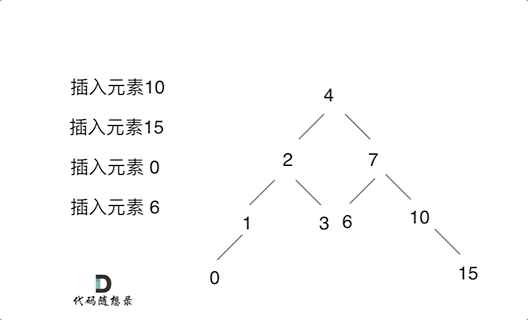
思路：

不需要调整二叉搜索树的结构，只要遍历二叉搜索树，找到空节点插入元素就可以了

递归
（1）确定递归函数参数以及返回值
参数：根节点，要插入的元素
返回值：TreeNode*
可以利用返回值完成新加入的节点与其父节点的赋值操作

TreeNode* insertIntoBST(TreeNode* root, int val)

（2）确定终止条件

当遍历的节点为NULL时，就是要插入节点的位置，并把插入的节点返回

if (root == NULL) {
	TreeNode* node = new TreeNode(val);
	return node;
}

把添加的节点返回给上一层，就完成了父子节点的赋值操作
（3）确定单层递归的逻辑

搜索树是有方向的，根据插入元素的数值，决定递归方向

if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);
return root;

下一层将加入节点返回，本层用root->left或者root->right将其接住

C++：

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if (root->val > val) {
            root->left = insertIntoBST(root->left, val);
        }
        if (root->val < val) {
            root->right = insertIntoBST(root->right, val);
        }
        return root;
    }
};

3 删除二叉搜索树中的节点

450.删除二叉搜索树中的节点

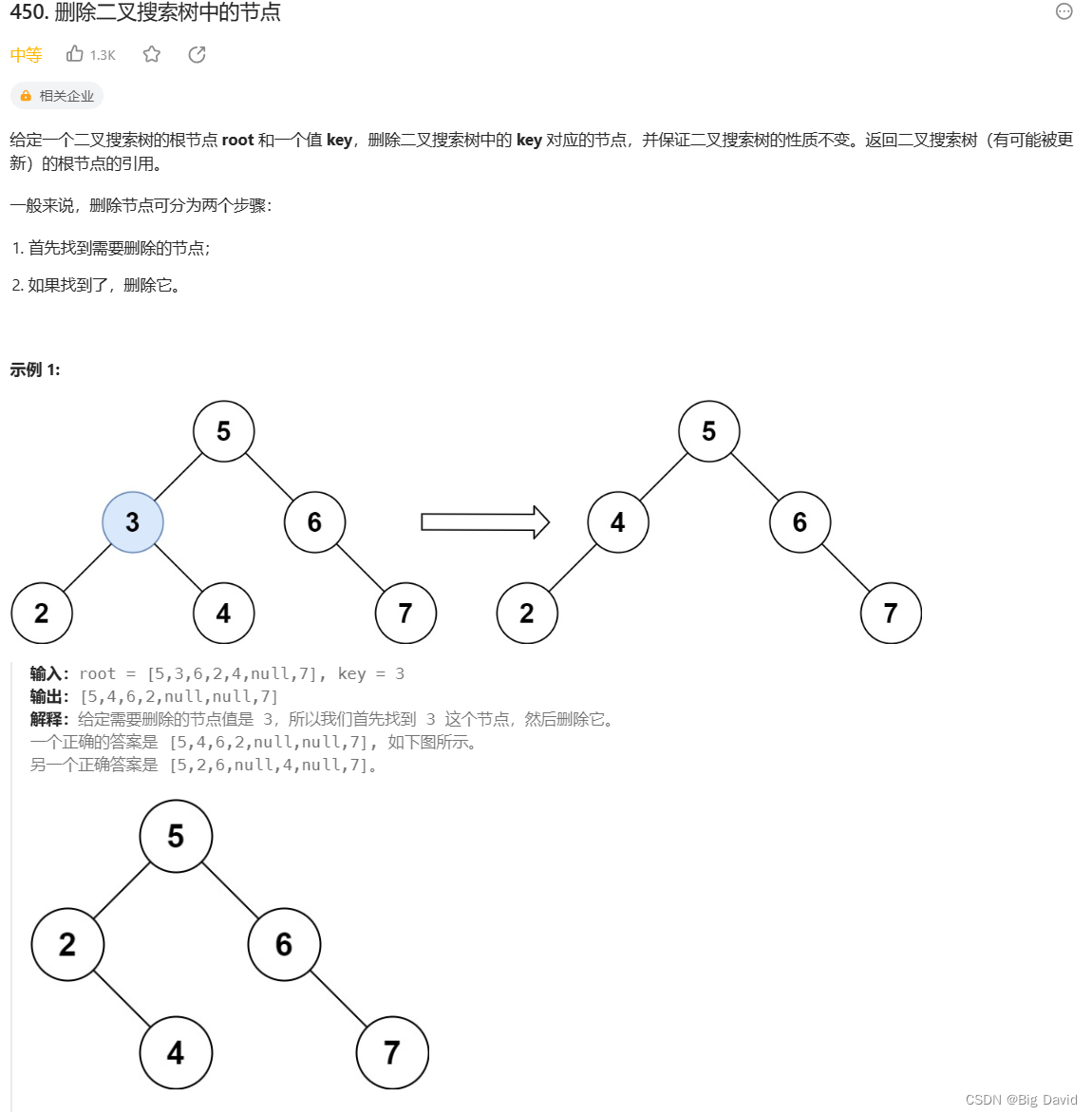
搜索树节点删除比节点增加复杂得多，有更多的情况需要考虑
递归法
（1）确定递归函数参数以及返回值
参数：根节点，要删除的值
返回值：TreeNode*

TreeNode* deleteNode(TreeNode* root, int key)

（2）确定终止条件
五种情况：

（1）没找到删除的节点，遍历到空节点直接返回
（2）左右孩子都为空（叶子节点），直接删除节点，返回NULL
（3）删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
（4）删除节点的左孩子不为空，右孩子为空，删除节点，返回左孩子为根节点
（5）左右孩子节点都不为空，删除节点的左子树头节点放到删除节点的右子树最左面节点的左孩子上，返回删除节点右孩子为新的根节点

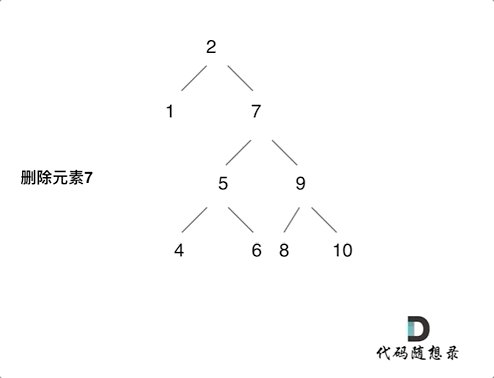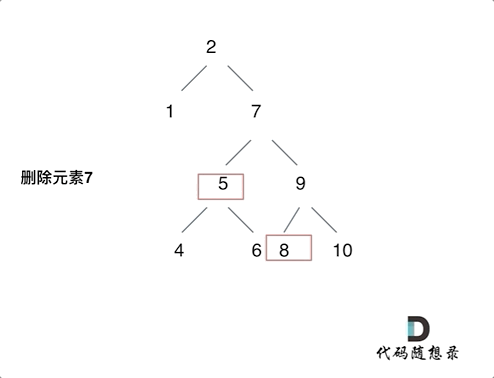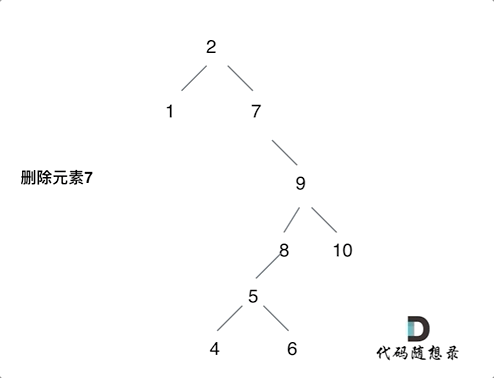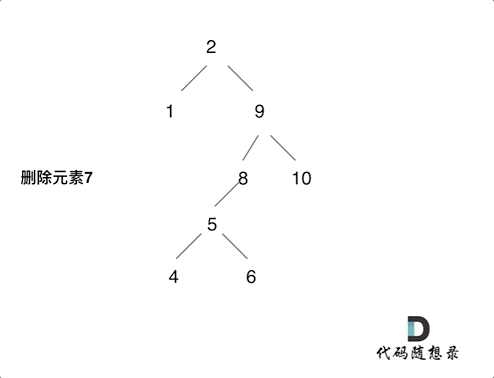
if (root == NULL) return root; // 1 没找到删除的节点
if (root->val == key) {
	// 2 左右孩子都为空（叶子节点）
	if (root->left == NULL && root->right == NULL) {
		delete root;
		return NULL;
	}
	// 3 删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
	else if (root->left == NULL && root->right != NULL) {
		TreeNode* node = root->right;
		delete root;
		return node;
	}
	// 4 删除节点的左孩子不为空，右孩子为空，删除节点，返回左孩子为根节点
	else if (root->left != NULL && root->right == NULL) {
		TreeNode* node = root->left;
		delete root;
		return node;
	}
	// 5 左右孩子节点都不为空，删除节点的左子树头节点放到删除节点的右子树最左面节点的左孩子上，返回删除节点右孩子为新的根节点
	else {
		TreeNode* cur = root->right;// 找右子树最左面的节点
		while (cur->left != NULL) {
			cur = cur->left;
		}
		cur->left = root->left;// 把要删除的节点（root）左子树放在cur的左孩子的位置
		TreeNode* tmp = root;// 把root节点保存一下，下面来删除
		root = root->right;// 返回旧root的右孩子作为新root
		delete tmp;// 释放节点内存
		return root;
	}
}

（3）确定单层递归的逻辑

if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;

C++：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == NULL) return NULL;// 第一种情况：没找到删除的节点，遍历到空节点直接返回
        if (root->val == key) {
            if (root->left == NULL && root->right == NULL) {// 第二种情况：左右孩子都为空（叶子节点）
                delete root;
                return NULL;
            }
            else if (root->left != NULL && root->right == NULL) { // 第三种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
                TreeNode* node = root->left;
                delete root;
                return node;
            }
            else if (root->left == NULL && root->right != NULL) {// 第四种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
                TreeNode* node = root->right;
                delete root;
                return node;
            }
            else {// 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
                TreeNode* cur = root->right;// 找右子树最左面的节点
                while (cur->left != NULL) {
                    cur = cur->left;
                }
                cur->left = root->left;// 把要删除的节点（root）左子树放在cur的左孩子的位置
                TreeNode* tmp = root; // 把root节点保存一下，下面来删除
                root = root->right;// 返回旧root的右孩子作为新root
                delete tmp;
                return root;
            }
        }
        if (root->left) root->left = deleteNode(root->left, key);
        if (root->right) root->right = deleteNode(root->right, key);
        return root;
    }
};

---

鼓励坚持十九天的自己😀😀😀