【python入门篇】─Python函数（函数的参数，匿名函数，递归函数）

一、函数的参数

1、位置参数

????????这是最常见的参数类型。函数定义时按照顺序列出的参数就是位置参数。调用函数时必须按照相同的顺序传递参数值。

# 位置参数，按照位置将实参依次赋予形参
def f1(a,b):
    print(a,b)


f1(10,20)

运行结果

2、默认参数

????????默认参数在函数定义时给定了一个默认值，如果在调用函数时没有提供该参数的值，函数将使用默认值。默认参数写在最后，且可以有多个

# 默认参数
# 形参有默认值，调用时可以没有实参，
# 如果调用时 传递实参，就是传递的实参
def f1(a,b,c=100,d=200):
    print(a,b,c,d)


f1(10,20,30)
f1(10,20,50,500)

print(10,20,30,sep="+")

运行结果

3、关键字参数

????????关键字参数允许在函数调用时使用参数名来指定参数的值，而不仅仅是位置。

# 关键字参数
# 通过指定将实参赋予那个形参，要求没有默认值的形参必须赋值
def f1(a,b,c=10,d=20):
    print(a, b,c,d)


f1(100, 200, d=400)

r = random.sample(["a", "b", "c"],2)
print(r)

运行结果

4、可变（元组）参数

????????可变（元组）参数，可以接受任意个数的参数，类型是元组，用*加形参代表可变元组参数，一般用*args，*args 接受实际参数传递参数的时候会转化为元组的形式

def f1(a, *args, b=20):
    print(a, b, args, type(args))


f1(10, 20, 30, 40, 50, 60, 70, 80,b=2000)

运行结果

5、可变字典参数

????????有时候我们不确定需要传递多少个参数给函数，这时可以使用可变参数。Python提供两种可变参数：*args（用于接收任意数量的位置参数）和**kwargs（用于接收任意数量的关键字参数）可变字典参数就是**kwargs，可以使用关键字赋值,关键字不能是真实形参

def f1(a, b, *args, **kwargs):
    print(a, b, args, kwargs, type(kwargs))


f1(10, 20, 30, 40, 50, c=70,d=80)

运行结果?

二、匿名函数

1、定义

????????在Python中，可以使用lambda关键字创建匿名函数（也称为“lambda函数”）。匿名函数可以作为参数传递给其他函数或直接调用。

注意事项：

①lambda只支持最简单最基本的函数写法，
②冒号左边是形参列表，多个参数用逗号隔开，
③冒号右边是返回值

1.1 定义一个简单的匿名函数案例

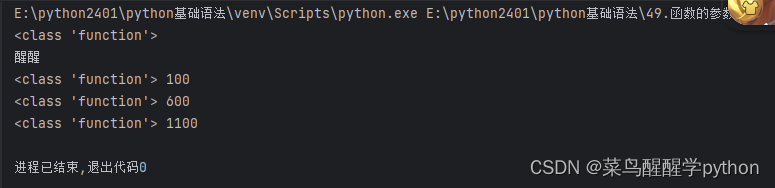
f2 = lambda:print("醒醒")
print(type(f2))
f2()

f3 = lambda :100
print(type(f3),f3())

f4 = lambda x:x+100
print(type(f4),f4(500))

f5 = lambda x,y:x + y
print(type(f5),f5(500,600))

运行结果

2、只能包含单个表达式，该表达式的结果将成为函数的返回值。

# 创建一个将两个数相加的匿名函数
add = lambda x, y: x + y
result = add(3, 4)
print(result)  # 输出：7

3、lambda函数没有名称，只能通过变量来引用它。

# 将匿名函数赋值给变量
multiply = lambda x, y: x * y
result = multiply(3, 4)
print(result)  # 输出：12

4、lambda函数可以作为其他函数的参数传递。

def calculate(func, x, y):
    result = func(x, y)
    print(f"The result is: {result}")

calculate(lambda x, y: x + y, 3, 4)  # 输出：The result is: 7
calculate(lambda x, y: x * y, 3, 4)  # 输出：The result is: 12

三、递归函数

1、定义

递归函数的定义 : 自己调用自己的函数就是递归，还有就是必须有递归出口

2、递归求和

# 计算1+2+3的和
def f(n):
    # 递归出口
    if n == 1:
        return 1
    else:
        # 自己调用自己
        return n + f(n-1)


r = f(3)
print(r)

3、递归求阶乘

# 5！= 5 * 4 * 3 * 2 * 1
def f(n):
    if n == 1:
        return 1
    else:
        return n * f(n-1)


r = f(5)
print(r)

4、递归求斐波那契

# 斐波那契数列
# 1 1 2 3 5 8 13 21... n

# def f(n):
#     if n == 1:
#         return 1
#     elif n == 2:
#         return 1
#     else:
#         return f(n-1) + f(n-2)
#
# r = f(9)
# print(r)

5、递归不是高性能的

6、递归有深度限制

import sys
# 获取递归深度
print(sys.getrecursionlimit())
sys.setrecursionlimit(2000) # 输出结果1000

超过这个深度就报错

print(sys.getrecursionlimit())
def f(n):
    # 递归出口
    if n == 1:
        return 1
    else:
        # 自己调自己
        return n * f(n-1)

r = f(1500)
print(r)