算法训练营Day29(回溯5)

发布时间：2024年01月02日

*?491.递增子序列力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

提醒

本题和大家刚做过的?90.子集II?非常像，但又很不一样，很容易掉坑里。?

①需要树层去重②必须递增

class Solution:
    def findSubsequences(self, nums):
        result = []
        path = []
        self.backtracking(nums, 0, path, result)
        return result
    
    def backtracking(self, nums, startIndex, path, result):
        if len(path) > 1:
            result.append(path[:])  # 注意要使用切片将当前路径的副本加入结果集
            # 注意这里不要加return，要取树上的节点
        
        uset = set()  # 使用集合对本层元素进行去重
        for i in range(startIndex, len(nums)):
            if (path and nums[i] < path[-1]) or nums[i] in uset:
                continue
            
            uset.add(nums[i])  # 记录这个元素在本层用过了，本层后面不能再用了
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()

提醒

本题重点感受一下，排列问题?与?组合问题，组合总和，子集问题的区别。?

? ?思考：为什么排列问题不用?startIndex?

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False

提醒

本题?就是 40.组合总和II?去重逻辑?和?46.全排列?的结合（多了去重的操作），可以先做一下，然后重点看一下此题拓展内容。

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        nums.sort()  # 排序
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False

拓展

used[i?-?1]?==?true?也行，used[i?-?1]?==?false?也行。

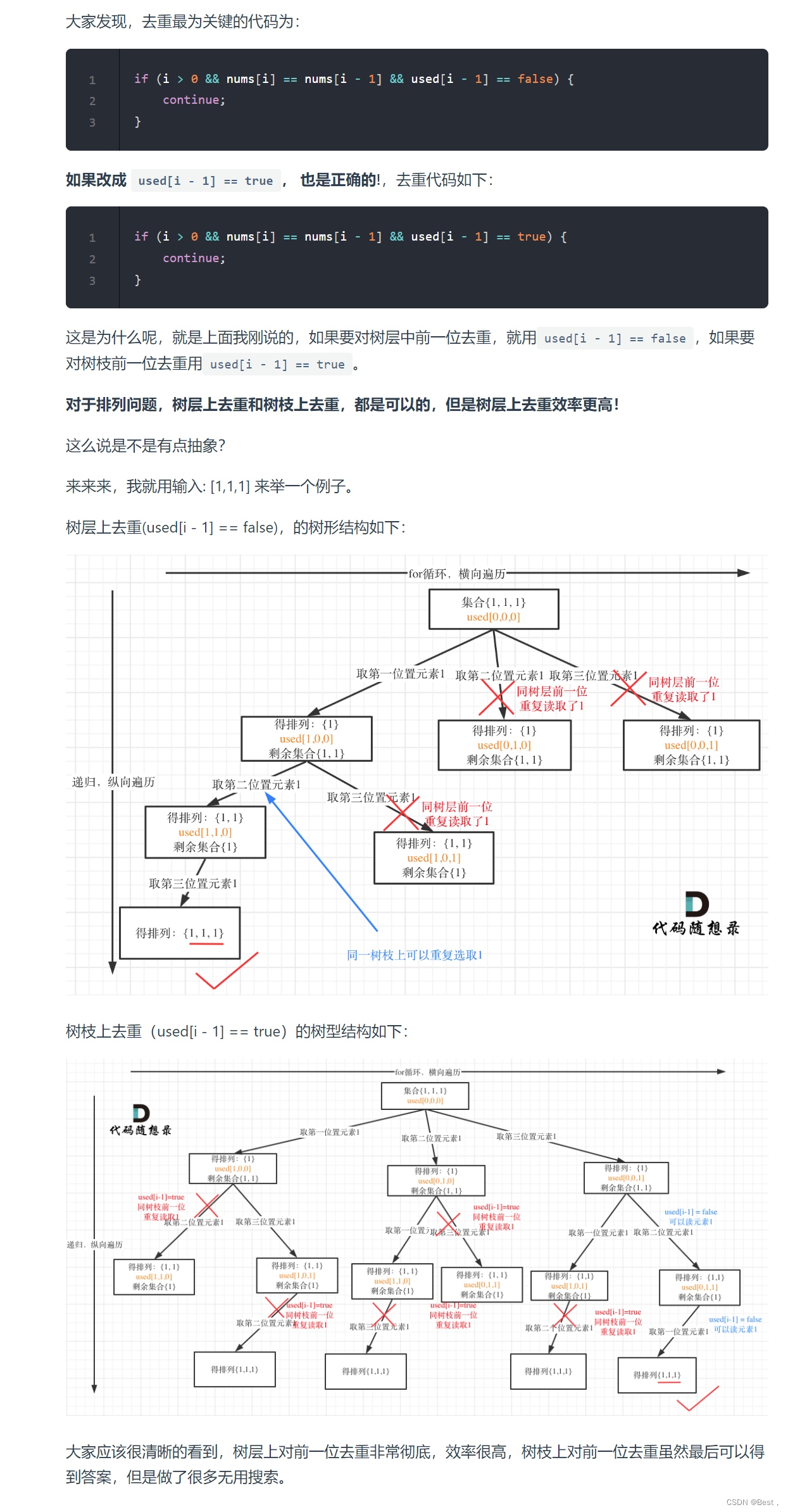
文章来源:https://blog.csdn.net/2301_79788081/article/details/135304659
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章