Python - 深夜数据结构与算法之 BFS & DFS
目录
一.引言
BFS 广度优先搜索与 DFS 深度优先搜索是树以及网格等相关题目最常见的方法之一,其通过不同的遍历方式对分叉结构进行遍历,对于树、图而言,其可以是二叉、多叉,其可以是上下左右,下面让我们深入了解下 BFS 与 DFS。
二.BFS 与 DFS 简介
1.Search 搜索

不论是 BFS 还是 DFS,它们都是数据结构节点的访问方式,为了效率足够高,我们希望每个节点访问且仅访问一次,因而衍生出了 DFS - Depth First Search 深度优先搜索与 BFS - Breadth First Search 广度优先搜索两种遍历方式。除此之外还有按照节点优先级访问的算法,不过需要特定的场景才会使用。?

2.DFS 深度优先
深度优先搜索,我们前面提到的二叉树的前中后序遍历都是深度优先搜索的一种,对于二叉树而言,其深度搜索的路径是向 Left 左子树和 Right 右子树递进,多叉树的话则是其 Children 节点集合,对于图而言,则是其他相邻的点 V,其通式可以参照下面的写法。
◆ 递归写法
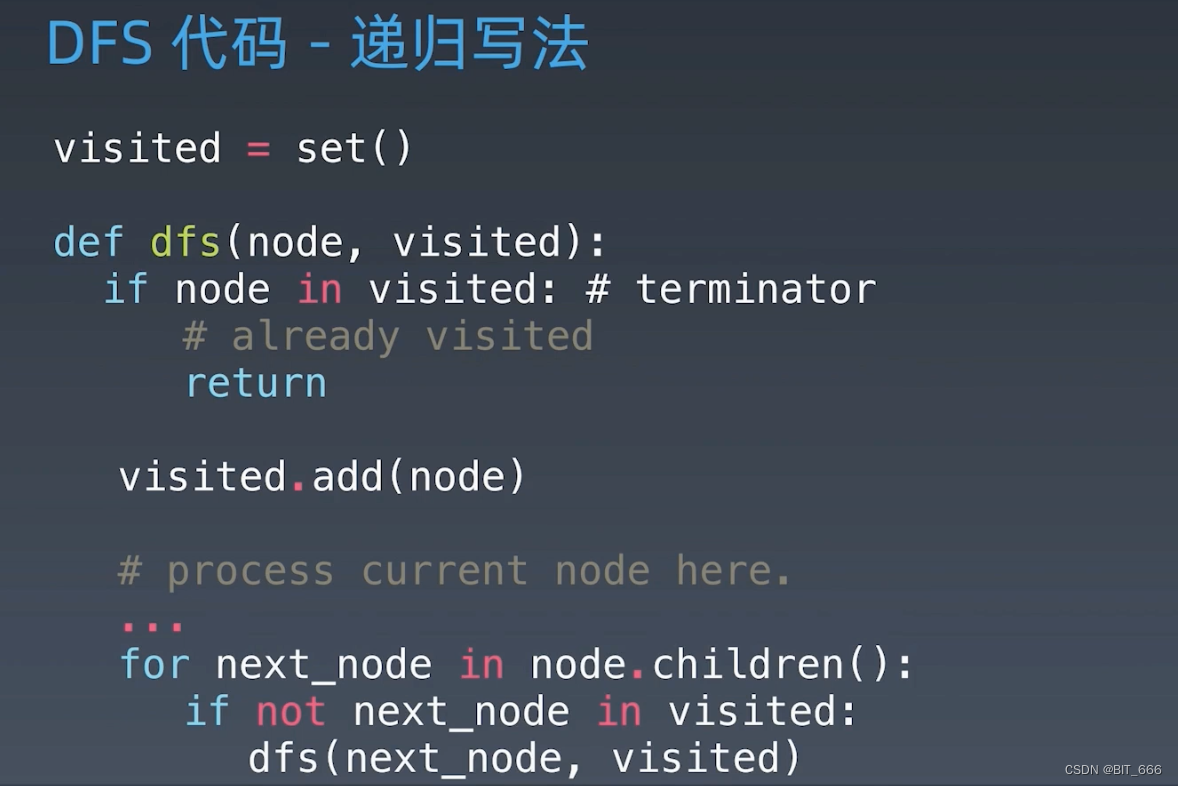
◆ 非递归写法
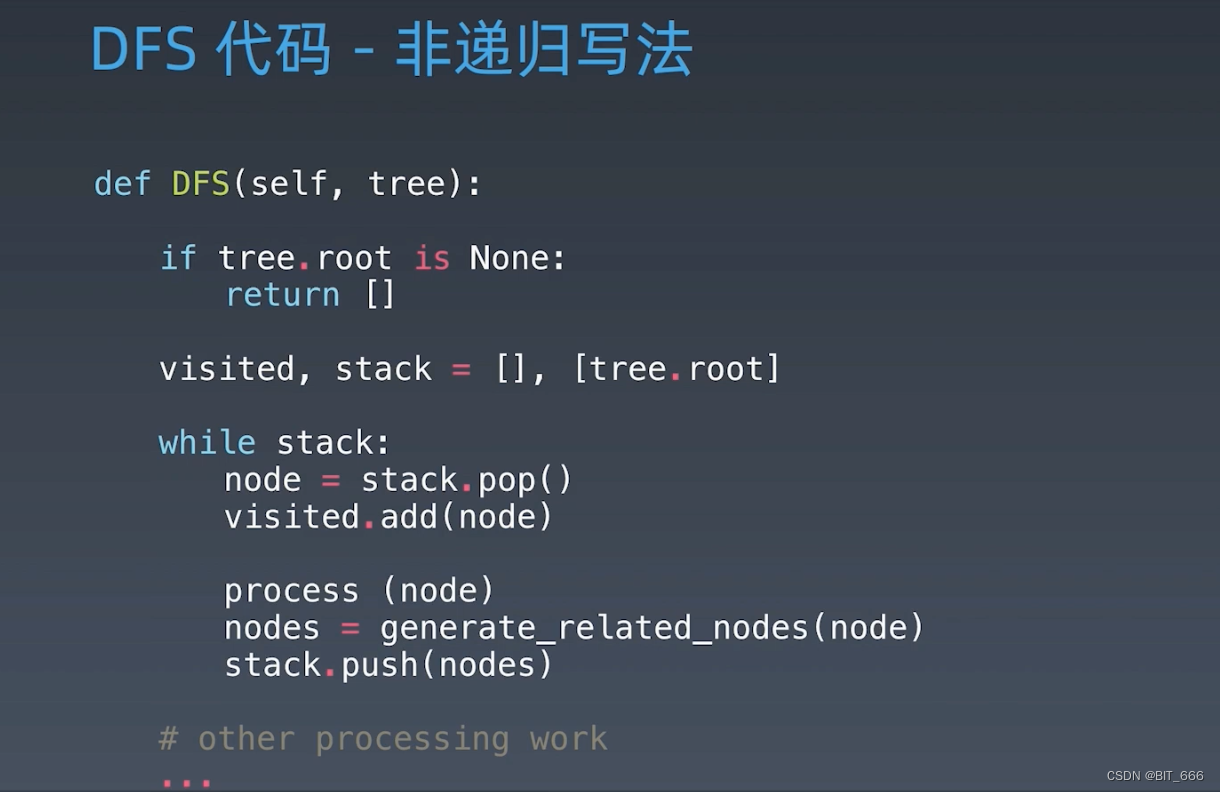
?◆ 树的遍历
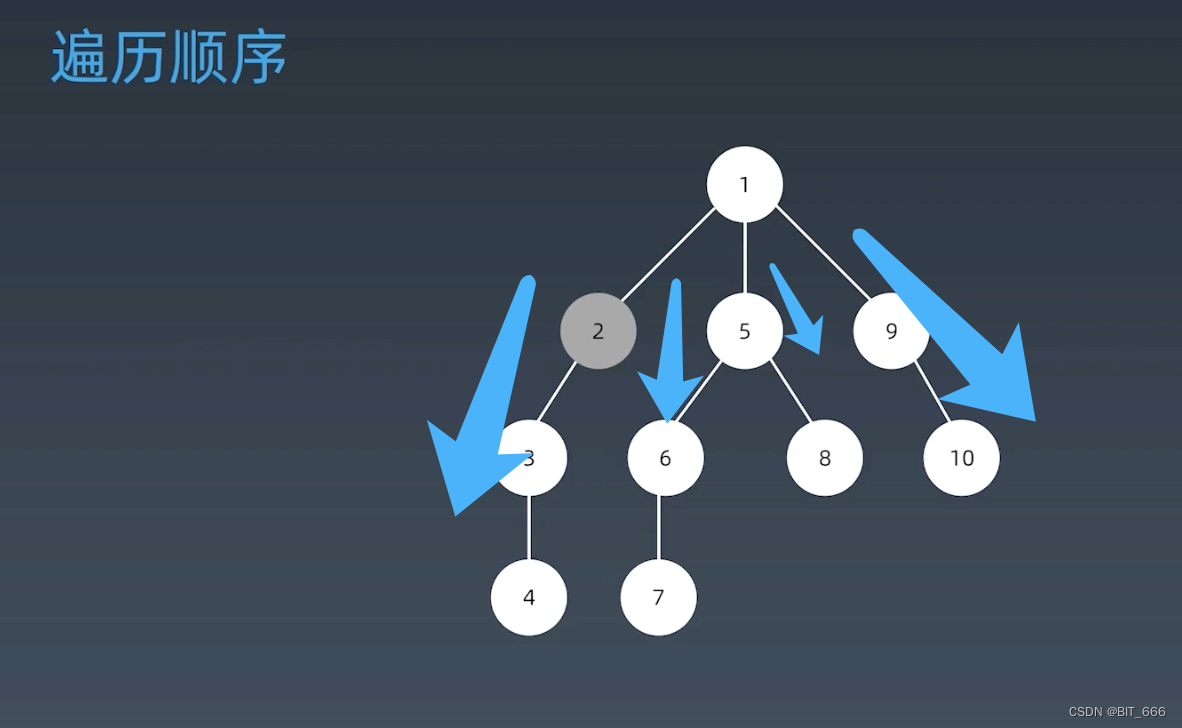
◆ 图的遍历?
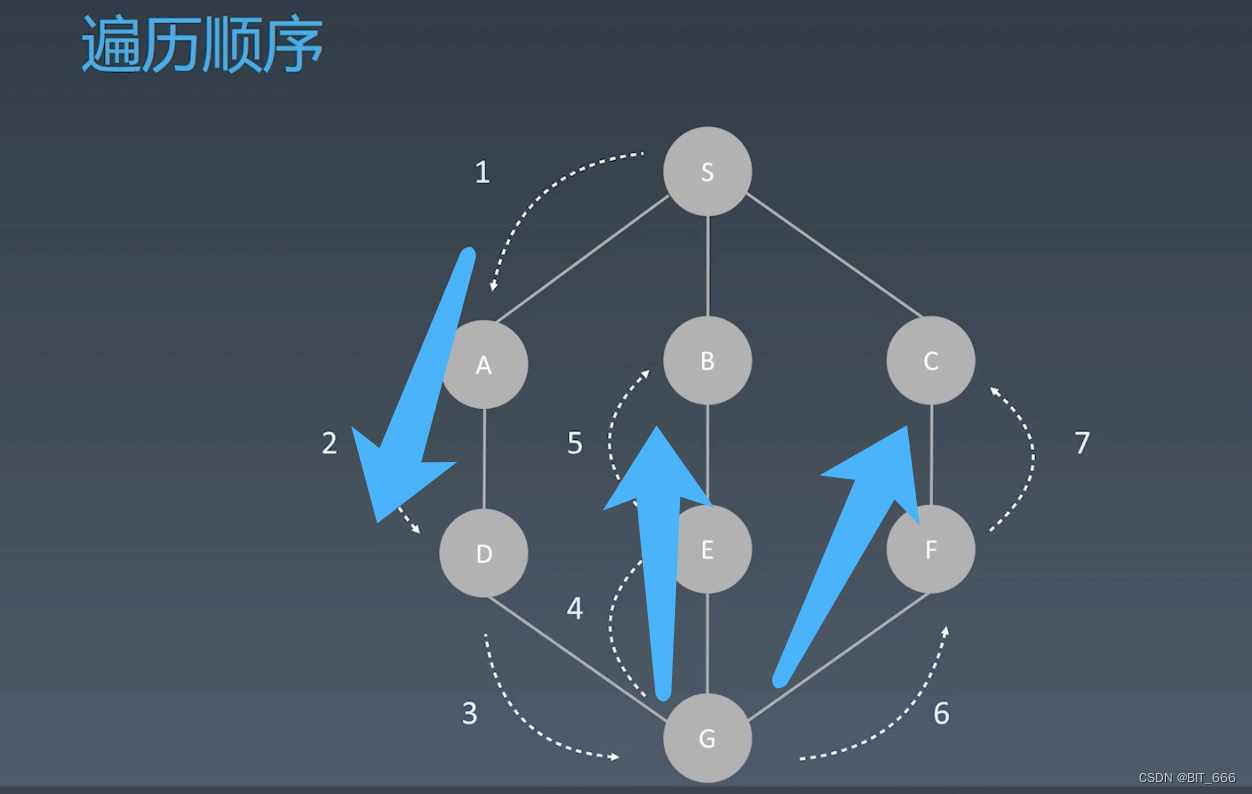
3.BFS 广度优先
广度优先与深度优先不同,其从每一层下探访问节点,就好比是一滴水波纹逐渐向下扩散,然后扩散到每一层的节点上。
◆ 树的遍历?
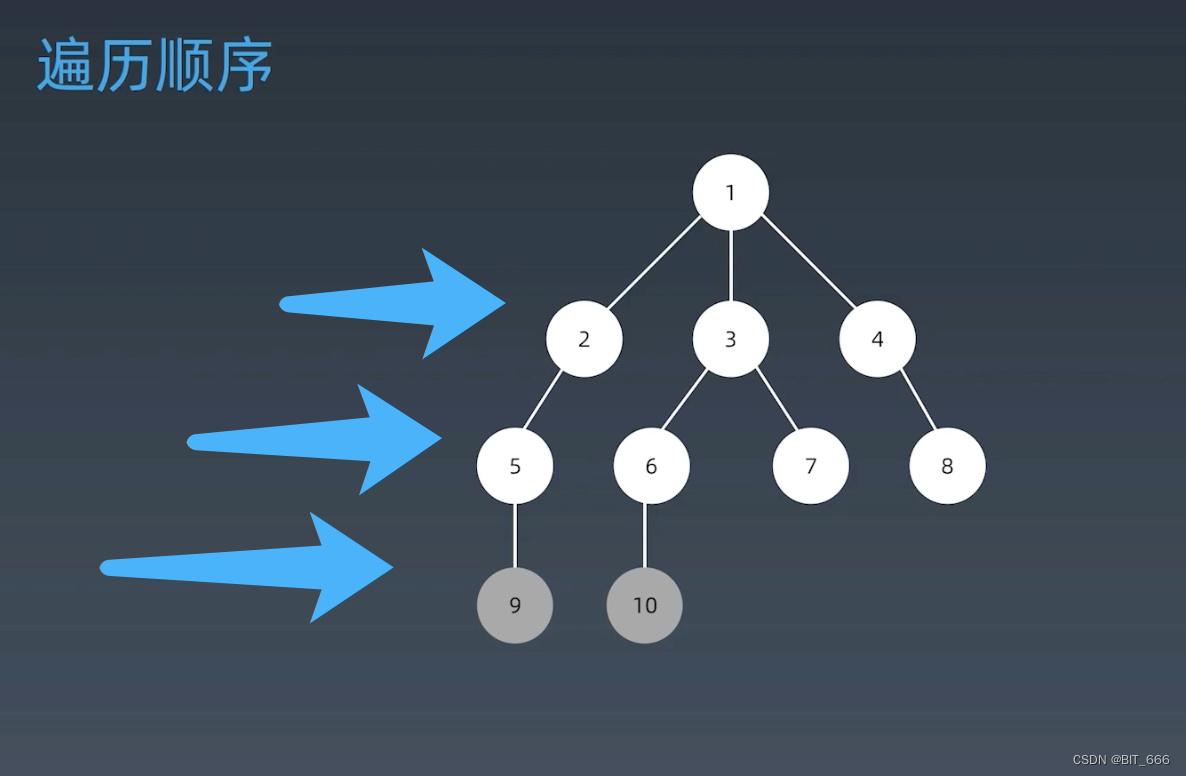
◆ 代码写法
这里的队列其实就是我们常用到的列表。注意这里的 queue pop 是先进先出的,大家要和上面的 stack.pop 区分开。
![]()
4.DFS & BFS
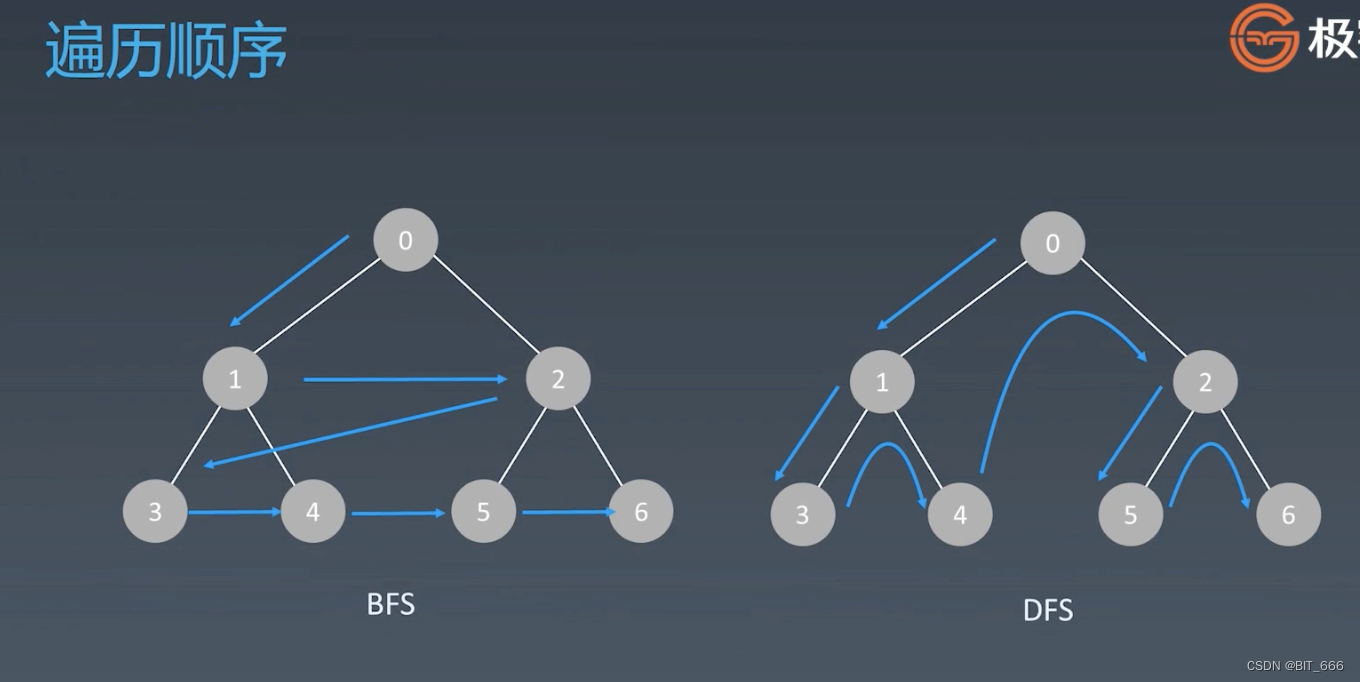
我们可以根据上面的图再理解下 DFS 与 BFS 的遍历方式,如果都是用 List 实现的话,BFS 是 Deque 先进先出,DFS 则是 Stack 后进先出。
三.经典算法实战
1.Generate-Parentheses [22]
括号生成:?https://leetcode.cn/problems/generate-parentheses/description/

◆?题目分析
这里可以看做是一颗二叉树,其每个节点可以分叉为 '(' 和 ')',我们需要遍历生成情况,并判断当前生成是否有效,再向下遍历。有效的条件有两个,一个是左括号一定是开头的第一个字符,另一个是左括号要和右括号数量一致。
◆?广度优先
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
res = []
def dfs(cur, left, right):
# 终止条件
if left == n and right == n:
res.append(cur)
# 左括号要在前面
if left < n:
bfs(cur + "(", left + 1, right)
# 右括号要比左括号小
if right < left:
bfs(cur + ")", left, right + 1)
dfs("", 0, 0)
return res
?DFS 遍历的模版,直接一层一层下去找,直到满足 2n 的条件。

◆?栈实现
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
res = []
queue = [("", 0, 0)]
while queue:
cur, left, right = queue.pop(0)
if left == right == n:
res.append(cur)
if left < n:
queue.append((cur + "(", left + 1, right))
if right < left:
queue.append((cur + ")", left, right + 1))
return resDFS、BFS 的几种模版一定要多多练习,手到擒来。
2.Level-Order-Travesal [102]
二叉树层序遍历:?https://leetcode.cn/problems/binary-tree-level-order-traversal
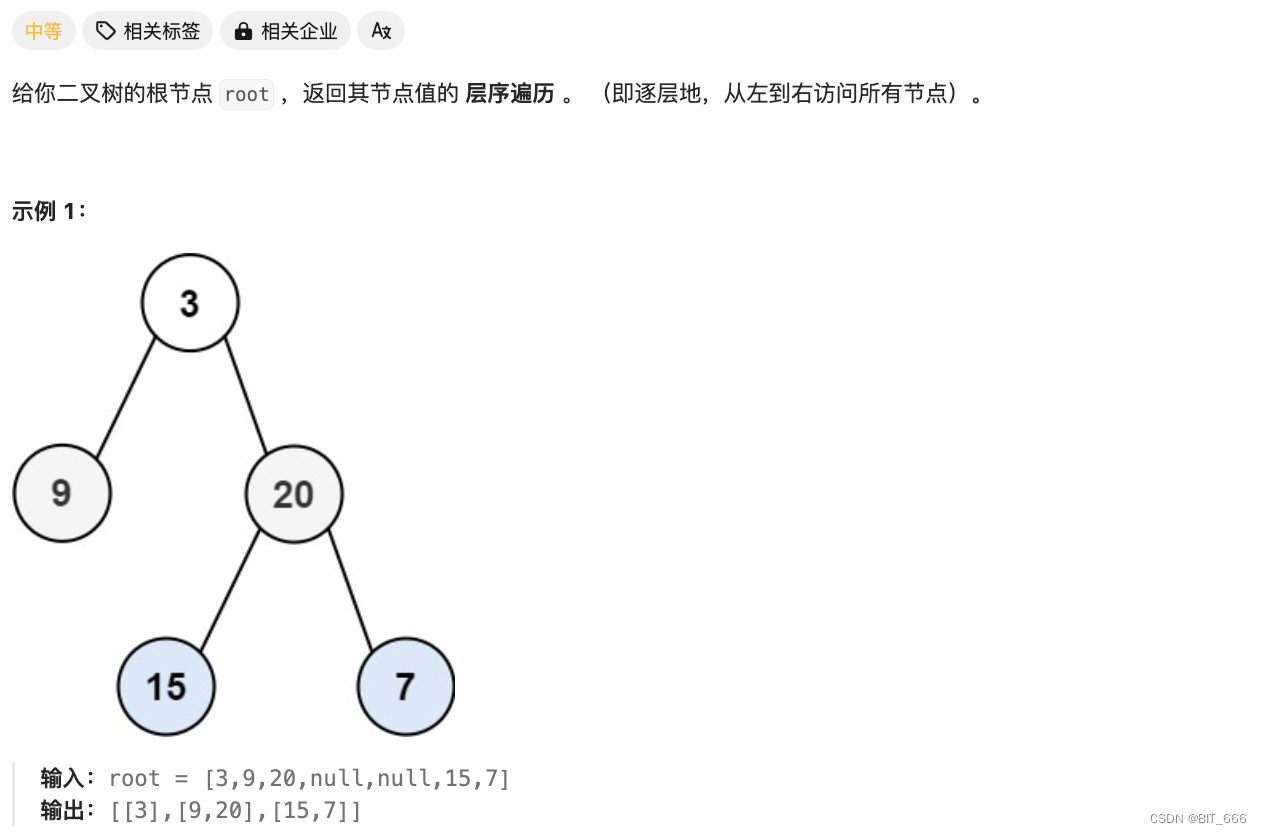
◆?题目分析
二叉树 BFS 遍历,这里要求我们逐层按列表返回而不是一个列表全部返回,所以我们在 BFS 套模版的基础上,还需要记录其 level 层的位置。
◆?广度优先
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
# 先进先出
queue = [(0, root)]
res = []
while queue:
# 记录对应的层次
index, cur = queue.pop(0)
if len(res) < index + 1:
res.append([])
res[index].append(cur.val)
# 添加层消息与节点
if cur.left:
queue.append((index + 1, cur.left))
if cur.right:
queue.append((index + 1, cur.right))
return res按层遍历,每层下探时增加 index 找到其在 res 中对应的 list 保存即可。?
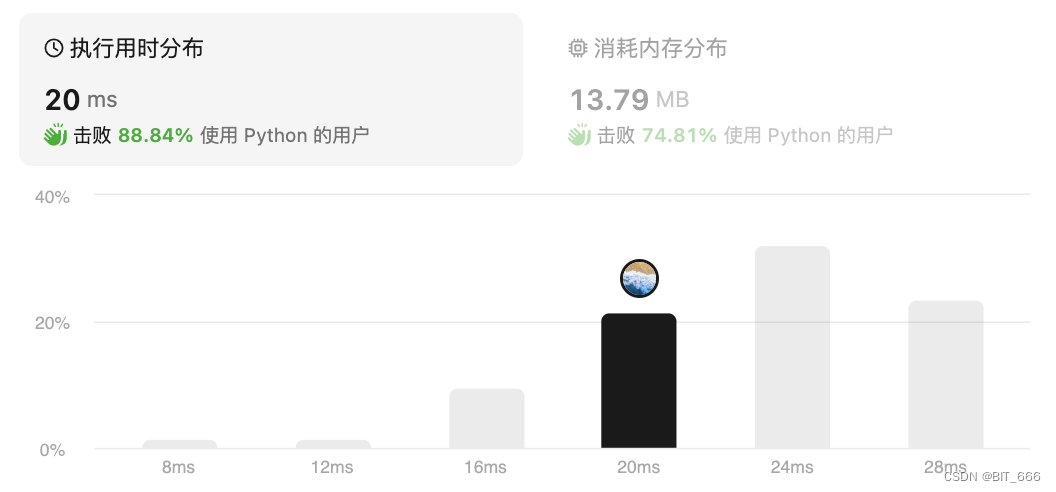
◆?深度优先
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
res = []
def dfs(root, level):
if not root:
return
if len(res) == level:
res.append([])
res[level].append(root.val)
# 通过 level 存储层的信息
if root.left:
dfs(root.left, level + 1)
if root.right:
dfs(root.right, level + 1)
dfs(root, 0)
return res层序遍历适合本题,但是深度遍历也可以实现,我们在向下探索的过程中可以获取当前的 level,只需将遍历到的结果对应的 level 找到即可。?

3.Word-Ladder [127]
单词接龙:?https://leetcode.cn/problems/word-ladder/description/

◆?题目分析
层序遍历的方法,类似前面的基因突变,这里可以理解为连续突变且每次可以突变 26 个字母。
◆?广度优先
class Solution(object):
def ladderLength(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: int
"""
# 去重使用
valid_word = set(wordList)
if endWord not in wordList or len(wordList) == 0:
return 0
queue = [(beginWord, 1)]
while queue:
new_queue = []
for word, step in queue:
# 停止条件
if word == endWord:
return step
# 处理当前元素
for i in range(len(word)):
# 突变每一个位置
for char in 'abcdefghijklmnopqrstuvwxyz':
# 去重优化
if char != word[i]:
new_word = word[:i] + char + word[i + 1:]
if new_word in valid_word:
valid_word.remove(new_word)
new_queue.append((new_word, step + 1))
queue = new_queue
return 0
这里 for char in 'abcd...' 可以使用 orc + chr 转换:
for char in range(ord('a'), ord('z') + 1):
print(chr(char))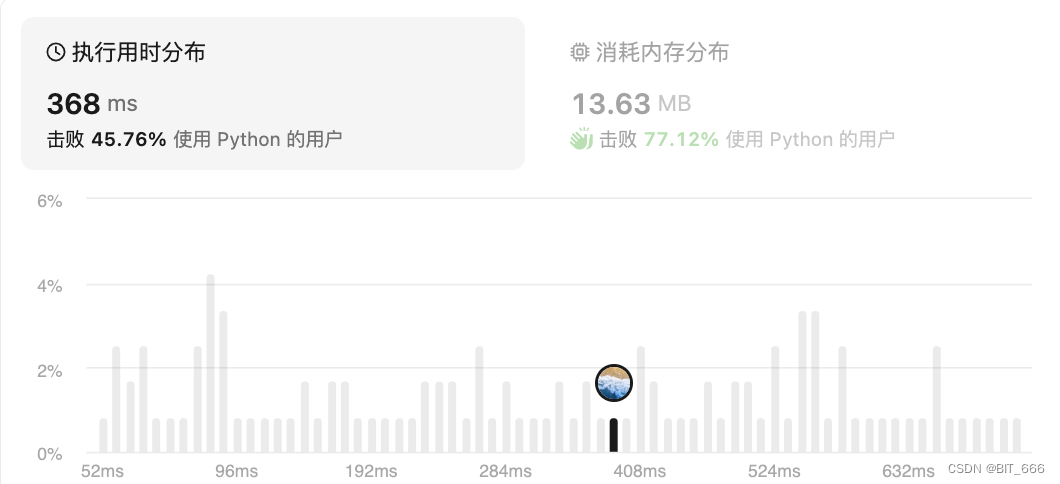
◆?双向 BFS
class Solution(object):
def ladderLength(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: int
"""
# 去重使用
valid_word = set(wordList)
if endWord not in wordList or len(wordList) == 0:
return 0
# 双向 BFS
begin, end, step = {beginWord}, {endWord}, 1
while begin and end:
if len(begin) > len(end):
begin, end = end, begin
# 存储下一层
next_level = set()
for word in begin:
for i in range(len(word)):
# a-z
for x in 'abcdefghijklmnopqrstuvwxyz':
# 节省无必要的替换
if x != word[i]:
new_word = word[:i] + x + word[i + 1:]
if new_word in end:
return step + 1
if new_word in valid_word:
next_level.add(new_word)
valid_word.remove(new_word)
begin = next_level
step += 1
return 0
为了加快搜素速度我们改写为双向 BFS,Begin-A-B-C-D-End 我们拆分为 Begin -> B,End -> B,两边同时检索,最终输出总的 step。这里我们尝试了 ord 的写法,但是时间复杂度没有上面的直接。
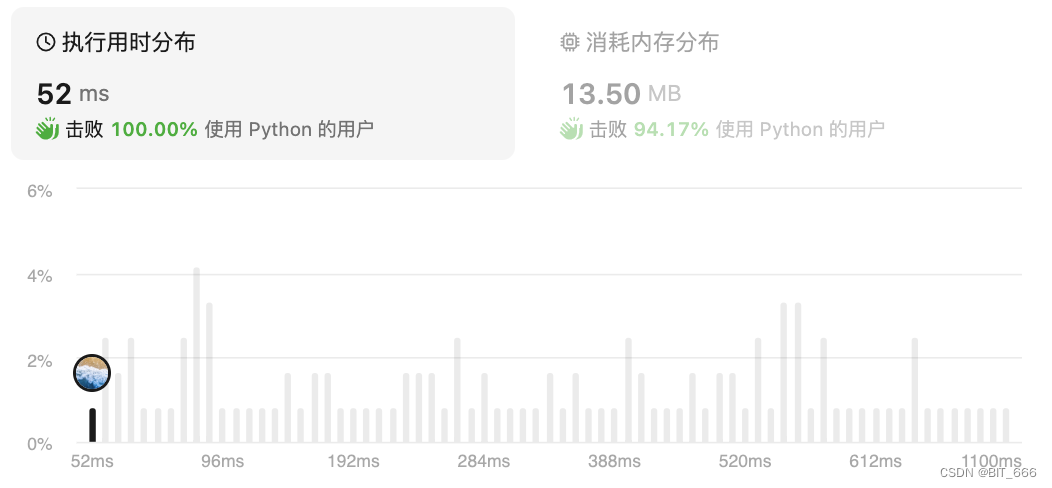
4.Num-Of-Islands [200]
岛屿数量:?https://leetcode.cn/problems/number-of-islands/description/

◆?题目分析
对于每个点 row col,其都有上下左右 4 个分叉点,我们可以作为四叉树遍历,通过 generate_related_nodes 方法生成其不同分叉,并判断是否可以联通 [row,col] == 1,最后遍历所有 gird 的点,看可以走通多少次返回 count 即可。

◆?深度优先
class Solution(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
# 异常情况
if not grid:
return 0
# 记录岛屿数量
numLand = 0
# 遍历并标记
for row in range(len(grid)):
for col in range(len(grid[0])):
if grid[row][col] == "1":
self.dfs(row, col, grid)
numLand += 1
return numLand
# 在网格索引范围内
def inArea(self, row, col, grid):
return 0 <= row < len(grid) and 0 <= col < len(grid[0])
def dfs(self, row, col, grid):
# 判断节点合法性
if not self.inArea(row, col, grid) or grid[row][col] != "1":
return
grid[row][col] = "2"
self.dfs(row + 1, col, grid)
self.dfs(row, col + 1, grid)
self.dfs(row - 1, col, grid)
self.dfs(row, col - 1, grid)继续 dfs 的条件是在 grid 内且值为 "1"。?
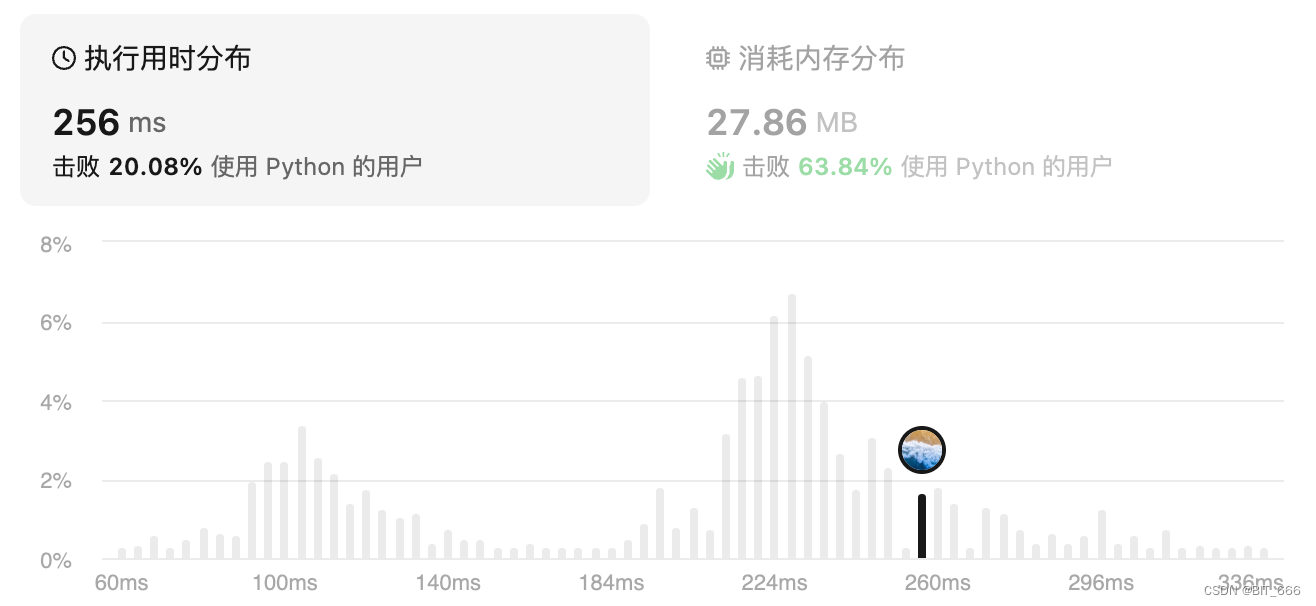
5.Min-Gene-Mutation [433]
最小基因变化:?https://leetcode.cn/problems/minimum-genetic-mutation/
◆?题目分析
题目给定了基因的 4 种类型 'ACGT',就像是 4 叉树一样,我们每次遍历有 4 个方向可以走,当前层遍历完再向下一个索引继续遍历,总共有 4^^8 种情况,由于有 bank 的限制,我们可以过滤掉多种情况。?
◆?广度优先
class Solution(object):
def minMutation(self, startGene, endGene, bank):
"""
:type startGene: str
:type endGene: str
:type bank: List[str]
:rtype: int
"""
# 没有基因库或最终突变不在基因库
if not bank or endGene not in bank:
return -1
queue = []
queue.append((startGene, 0))
# 记录基因是否有效
valid_bank = set(bank)
while queue:
# 获取当前步数
gene, step = queue.pop(0)
# 突变每一个位置
for i in range(len(gene)):
for g in 'ACGT':
# 从第一个位置开始,每个突变一次
if g != gene[i]:
change_gene = gene[:i] + g + gene[i + 1:]
if change_gene == endGene:
return step + 1
elif change_gene in valid_bank:
queue.append((change_gene, step + 1))
valid_bank.remove(change_gene)
return -1
?判断 g != gene[i] 减少相同字符的替换。
6.Largest-Values [515]
每层的最大值:?https://leetcode.cn/problems/find-largest-value-in-each-tree-row/
◆?题目分析
层序遍历,找到每一层的最大值即可,也可以深度遍历,记录即可。
◆?广度优先
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def largestValues(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
if not root:
return []
queue = [root]
res = []
while queue:
cur_max = -99999999999
new_queue = []
# 遍历每一层
for i in range(len(queue)):
if queue[i]:
cur_max = max(cur_max, queue[i].val)
if queue[i].left:
new_queue.append(queue[i].left)
if queue[i].right:
new_queue.append(queue[i].right)
res.append(cur_max)
queue = new_queue
return res
空间复杂度主要使用了 queue,其余操作主要在计算 max。?
◆?深度优先
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def largestValues(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res = []
def dfs(root, level):
# 停止条件
if not root:
return
# 当前层逻辑
if len(res) == level:
res.append(-9999999999)
res[level] = max(res[level], root.val)
# 下一层
if root.left:
dfs(root.left, level + 1)
if root.right:
dfs(root.right, level + 1)
dfs(root, 0)
return res同理,DFS 时可以使用 level 保存层的信息,我们通过 level 与数组建立关系构造 max 即可。
7.Mine-Clearance [529]
扫雷游戏:?https://leetcode.cn/problems/minesweeper/description/?

◆?题目分析
给定初始二维数组和起点,返回修改后的二维数组。若起点处是雷,即 ‘M’,直接将其修改为 'X',游戏结束;若起点处是空,即 ‘E’,则从起点开始向 8 邻域中的空地搜索,直到到达邻接💥的空地停止。和二叉树从根结点开始搜索,直到达到叶子节点停止,是几乎一样的,可以使用 BFS/DFS,但是 BFS 需要记录重复的节点。
◆?深度优先?
class Solution(object):
dx = [1, 1, -1, -1, 1, -1, 0, 0]
dy = [1, -1, 1, -1, 0, 0, 1, -1]
def updateBoard(self, board, click):
"""
:type board: List[List[str]]
:type click: List[int]
:rtype: List[List[str]]
"""
# 空盘
if not board:
return []
# 空点
if not click:
return board
# 点击位置
row = click[0]
col = click[1]
# 💥
if board[row][col] == "M":
board[row][col] = "X"
else:
# DFS
self.dfs(row, col ,board)
return board
def dfs(self, row, col, board):
if not self.inArea(row, col, board):
return
# 周围是否有雷
count = 0
for i in range(8):
x = row + self.dx[i]
y = col + self.dy[i]
if self.inArea(x, y, board) and board[x][y] == "M":
count += 1
if count > 0:
board[row][col] = str(count)
return
# 周围没雷标记为 B
board[row][col] = 'B'
for i in range(8):
x = row + self.dx[i]
y = col + self.dy[i]
if self.inArea(x, y, board) and board[x][y] == "E":
self.dfs(x, y, board)
def inArea(self, row, col, board):
return 0 <= row < len(board) and 0 <= col < len(board[0])再套一下 DFS 的模版:
终止条件 - 当前 row/col 周围存在雷即 'M'
处理逻辑 - 有雷更新 cnt、没雷标记为 'B'
下探逻辑 - 上下左右撇那八个点进行多叉寻找
四.总结
虽然 BFS、DFS 的模版很简单,但是怎么和实际的题目联系在一起还需要多多实践,多多练习,上面一些题目是为了 BFS、DFS 而 BFS、DFS 实际上更有效率更优的算法,大家也可以到官网参考题解,更进一步。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 编写一个简单的服务和客户端(C++)
- 搭建属于自己的内容付费平台:开发知识付费APP教学
- MinGW64&CMake编译3D模型导出工具assimp.exe
- springboot/java/php/node/python婚纱影楼管理系统【计算机毕设】
- 基于SSM的实践项目管理系统设计与实现
- 30、商城系统(十二):性能调优:Jmeter压测,jvisualvm性能监控,nginx动静分离,堆溢出解决方案
- Java 实现汉字转拼音带音调
- 实战Python快速排序:深入学习算法步骤
- 如何在Java中管理内存和垃圾回收?解释ClassLoader的工作原理?
- TypeScript入门实战笔记 -- 01 如何快速搭建 TypeScript 学习开发环境?
