LeetCode 每日一题 Day 17 || 二分
发布时间:2023年12月19日
1901. 寻找峰值 II
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
示例 1:
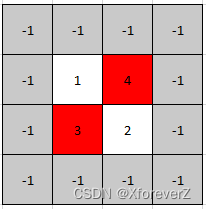
输入: mat = [[1,4],[3,2]]
输出: [0,1]
解释: 3 和 4 都是峰值,所以[1,0]和[0,1]都是可接受的答案。
示例 2:
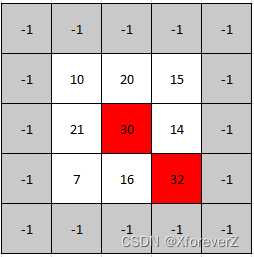
输入: mat = [[10,20,15],[21,30,14],[7,16,32]]
输出: [1,1]
解释: 30 和 32 都是峰值,所以[1,1]和[2,2]都是可接受的答案。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105任意两个相邻元素均不相等.
先给出代码:
class Solution {
public:
std::vector<int> findPeakGrid(std::vector<std::vector<int>>& mat) {
int m = mat.size();
int n = mat[0].size();
int left = 0, right = n - 1;
while (left < right) {
int mid = left + (right - left) / 2;
int maxRow = 0;
for (int i = 0; i < m; ++i) {
if (mat[i][mid] > mat[maxRow][mid]) {
maxRow = i;
}
}
if (mat[maxRow][mid] < mat[maxRow][mid + 1]) {
left = mid + 1;
} else {
right = mid;
}
}
int peakRow = 0;
for (int i = 0; i < m; ++i) {
if (mat[i][left] > mat[peakRow][left]) {
peakRow = i;
}
}
return {peakRow, left};
}
};
二分找峰值,先找到当前列最大所在行,然后比较该行和相邻列的值,确定二分方向之后峰值就好找了。
文章来源:https://blog.csdn.net/m0_73814009/article/details/135091547
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【PHP进阶教程】手把手教你实现用户登录验证(附实战代码)
- 微软Microsoft二面面试题分享&通过总结(不是标准答案分享
- TS学习笔记一:认识TS及环境准备
- 五、程序流程结构(1)选择结构——三目运算符
- C++图论之强连通图
- 数据库事务的特性
- docker-compose部署各个软件
- 10000字讲解TCP协议(确认应答,超时重传,三次握手,四次挥手等等众多机制)以及UDP协议(UDP报文,校验和)
- 从0开始学前端第二天
- 【Emgu.CV教程】第24篇 、色彩处理之LUT()查找表转换颜色