c语言第二次测试错题整理

5.1：

?5.4：

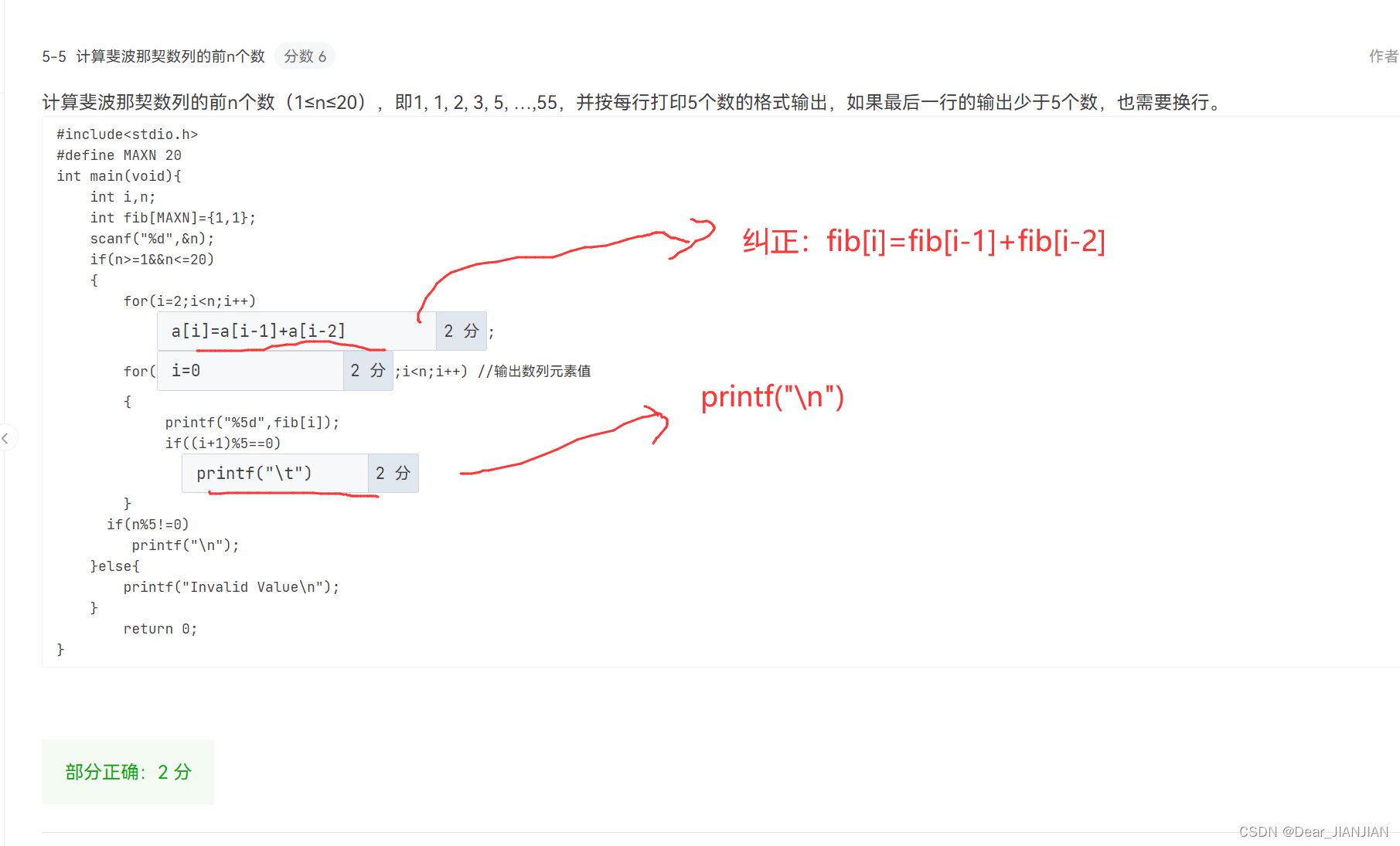
5.5：

7.1：

#include <stdio.h>
int main()
{
    double n;
    scanf("%lf",&n);
    double fenmu=1.0;
   double fenzi=1.0;
    double sum=1.0;
    int k=1;
    while((fenzi/fenmu)>=n)
    {
        fenzi=fenzi*k;
        fenmu=fenmu*(2*k+1);
        sum=sum+(fenzi/fenmu);
        k++;
    }
    printf("%.6f",2*sum);
    return 0;
}

参考：7-15 计算圆周率（PTA题库）_pta计算圆周率-CSDN博客文章浏览阅读2.2k次，点赞5次，收藏12次。根据下面关系式，求圆周率的值，直到最后一项的值小于给定阈值。输入格式：输入在一行中给出小于1的阈值。输出格式：在一行中输出满足阈值条件的近似圆周率，输出到小数点后6位。输入样例：0.01输出样例：3.132157错误代码：#includeint main(){ int n = 1, s = 1, k = 1.0; float x, y = 1.0, sum = 1.0;_pta计算圆周率https://blog.csdn.net/m0_61146840/article/details/124984806

错误示范：

//错误示范：
#include<stdio.h>
int main()
{
        int n = 1, s = 1, k = 1.0;
        float x, y = 1.0, sum = 1.0;
        scanf_s("%f", &x);
        for (n; y > x; n++) {
               s = s * (2 * n + 1);
               y = 1.0 * k / s;
               sum = sum + y;
               k = k * (n + 1);
        }
        printf("%.6f\n", sum * 2);
        return 0;
}

正确代码：

//正确代码
#include<stdio.h>
int main()
{
	int n = 1, s = 1, k = 1.0;
	float x, y = 1.0, sum = 1.0;
	scanf("%f", &x);
 
	for (n; y > x; n++) {
		y = y * n / (2*n + 1);
		sum = sum + y;
	}
	printf("%.6f\n", sum * 2);
	return 0;
}

分析：

一开始采用分子和分母分开运算的算法，编译未通过，显示n的阶乘超长整数，刚开始没搞明白，以为再用一种长整型的方式进行定义即可，后来发现还是不行，是因为n可以无穷大的，根本没有能存放它的变量，所以就不能用现有的算法进行计算，改变思路，对分子分母同时运算，就不会超长整型了。

总之：

我那样写不对！！！！?

?7.2：

#include <stdio.h>
int main()
{
    int i;
    int j;
    int n;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
    {
        
        for(j=1;j<=i;j++)
        {
            printf("%d*%d=%-4d",j,i,j*i);
            if(j==i)
            {
                printf("\n");
            }
        }
        
    }
    return 0;
}

?

?

7.3：

?

#include <stdio.h>
int main()
{
    int n;
    scanf("%d\n",&n);

    int i;
    char xing;
    double high=0;
   double high_2=0;
    for(i=0;i<n;i++)
    {
     
        //scanf("%c %lf\n",&xing,&high);
        scanf("%c %lf\n",&xing,&high);
        if(xing=='F')
        {
             high_2=high*1.09;  
            printf("%.2f\n",high_2);
        }else if(xing=='M'){
            high_2=high/1.09;
            printf("%.2f\n",high_2);
        }
    }
    return 0;
}

?

7-5：

#include <stdio.h>
int main()
{
    char a[100];
    gets(a);
    int i;
    int blank=0;
    int digit=0;
    int other=0;
    for(i=0;i<100;i++)
    {
       if(a[i]>='0'&&a[i]<='9')
       {
            digit++;
       }else if(a[i]==' ')
       {
            blank++;
       }else
       {
           other++;    
       }
       if(a[i]=='\0')
       {
            break;
       }
    }
    printf("blank = %d, digit = %d, other = %d",blank,digit,other-1);
    return 0;
}

?

?