Numpy入门

前言

---

学习本内容，需要对Python的语法有基本的了解，同时要会使用jupyter notebook。本文章中的Python代码，大多数都会在jupyter notebook上运行并展示。

---

1. Numpy介绍

---

1. Numpy是什么？

Numpy（Numerical Python的缩写）：

• 一个开源的Python科学计算库。
• 使用Numpy可以方便的使用数组、矩阵进行计算。
• 包含线性代数、傅里叶变换、随机数生成等大量函数。

2. 为什么使用Numpy？

对于同样的数值计算任务，使用原生Python肯定是可以实现的，但使用Numpy比使用原生Python有两个很大的优点：

• 代码更加简洁：Numpy直接以数组、矩阵为粒度计算，并且支持大量的数学函数，而Python需要用for循环从底层实现；
• 性能更高效：Numpy的数组存储效率和输入输出计算性能，比Python使用List或者嵌套List要好很多；

注：1. Numpy的数据存储和Python原生的List是不一样的；
注：2. Numpy的大部分代码都是C语言实现的，所以Numpy的效率很高。

Numpy是Python各种科学类库的基础库：

• 例如：SciPy、Scikit-learn、Tensorflow、PaddlePaddle等。

3. Numpy与原生Python的性能对比

需求：实现两个数组的加法，数组A是1~N数字的平方，数组B是1~N数字的立方。

导入numpy，并查看版本信息：

In [1]: import numpy as np

In [2]: np.__version__ # 查看numpy的版本
Out[2]: '1.24.3'

原生Python实现：

In [3]: def python_sum(n):
   		"""
        python 实现数组的加法
        n 为数组的长度
        """
        a = [i**2 for i in range(n)]
        b = [i**3 for i in range(n)]
        c = []
        for i in range(n):
            c.append(a[i] + b[i])
        return c
    
In [4]: # 测试
   		python_sum(10)
Out[4]: [0, 2, 12, 36, 80, 150, 252, 392, 576, 810]

Numpy实现：

In [5]: def numpy_sum(n):
    	"""
    	Numpy 实现数组的加法
    	n 为数组的长度
    	"""
    	a = np.arange(n) ** 2
    	b = np.arange(n) ** 3
    	return a + b
    	
In [6]: # 测试
		numpy_sum(10)
Out[6]: array([  0,   2,  12,  36,  80, 150, 252, 392, 576, 810])

性能对比：

In [7]: # 执行1000次
		%timeit python_sum(1000)
Out[7]: 257 μs ± 2.06 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

In [8]: %timeit numpy_sum(1000)
Out[8]: 8.59 μs ± 181 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

In [9]: # 执行10万次
		%timeit python_sum(10*10000)
Out[9]: 32.4 ms ± 232 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [10]: %timeit numpy_sum(100000)
Out[10]: 345 μs ± 2.08 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

In [11]: # 执行1000万次
		 %timeit python_sum(1000*10000)
Out[11]: 3.56 s ± 45.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [12]: %timeit numpy_sum(1000*10000)
Out[12]: 69 ms ± 459 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

注：%timeit 会让后面的代码执行多次并求平均执行时间。

使用可视化工具直观感受一下：（这一块不理解没有关系，跟着敲就行）

In [13]: # 将运行时间存起来，单位是us
		 pytimes = [257, 32.4*1000, 3.56*1000*1000]
		 nptimes = [8.59, 345, 69*1000]

In [14]: import pandas as pd

In [15]: df = pd.DataFrame({"pytimes":pytimes,"nptimes":nptimes,})

In [16]: %matplotlib inline
		 df.plot.bar()   # 使用柱状图显示

---

2. Numpy中的array

---

1. array对象的背景：

• Numpy的核心数据结构，就叫array，就是数组。array对象可以是一位数组，也可以是多维数组；
• Python的List也可以实现相同的功能，但是array优点在于性能好、包含数组元数据信息、有大量的便捷函数；
• Numpy已成为Scipy、pandas、Scikit-learn、Tensorflow、PaddlePaddle等框架的“通用底层语言”；
• Numpy的array继而Python的List的一个区别是，它的元素必须都是同一种数据类型，比如都是数字int类型，这也是Numpy高性能的一个原因。

2. 创建array的方法：

• 从Python的列表List和嵌套列表创建array；

In [1]: import numpy as np

In [2]: # 创建一个一维数组，也就是Python的单元素List
		x = np.array([1, 2, 3, 4, 5, 6, 7, 8])

In [3]: x
Out[3]: array([1, 2, 3, 4, 5, 6, 7, 8])

In [4]: # 创建一个二维数组，也就是Python中的嵌套List
		X = np.array(
    		[
        		[1,2,3,4],
        		[5,6,7,8]
    		]
		)

In [5]: X
Out[5]: array([[1, 2, 3, 4],
        	   [5, 6, 7, 8]])

• 使用预定函数arange、ones/ones_like、zeros/zeros_like、full/full_like、eye等函数创建；

1） 使用arange创建数字序列：arange(start, stop, step, dtype=None)，这个函数不管怎么传参，返回的都是一个一维向量。

In [6]: np.arange(10)
Out[6]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [7]: np.arange(2, 10, 2)
Out[7]: array([2, 4, 6, 8])

2）使用ones创建全是1的数组：np.ones(shape, dtype=None, order='C')。

In [8]: np.ones(10)   # 创建一维数组，大小为10
Out[8]: array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

In [9]: np.ones((2,3)) # 创建二维数组，2 行 3 列
Out[9]: array([[1., 1., 1.],
       		   [1., 1., 1.]])

3）使用ones_likes创建形状相同的数组：ones_likes(shape, dtype=float, order='C')。

In [10]: np.ones_like(x)  # 使用 x 的形状创建数组，里面全是 1
Out[10]: array([1, 1, 1, 1, 1, 1, 1, 1])

In [11]: np.ones_like(X) # 使用 X 的形状创建数组
Out[11]: array([[1, 1, 1, 1],
       			[1, 1, 1, 1]])

4）使用zeros创建全是0的数组：np.zero(shape, dtype=None, order='C')。

In [12]: np.zeros(10)
Out[12]: array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

In [13]: np.zeros((2, 4))
Out[13]: array([[0., 0., 0., 0.],
       			[0., 0., 0., 0.]])

5）使用zeros_like创建形状相同的数组：np.zeros_like(a, dtype=None)。

In [14]: np.zeros_like(x)
Out[14]: array([0, 0, 0, 0, 0, 0, 0, 0])

In [15]: np.zeros_like(X)
Out[15]: array([[0, 0, 0, 0],
       			[0, 0, 0, 0]])

6）使用empty创建全是0的数组：empty(shape, dtype=float, order='C')，数据是未初始化的，里面的值可能是随机值，不要用。

In [16]: np.empty(10)
Out[16]: array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

In [17]: np.empty((2, 4))
Out[17]: array([[0., 0., 0., 0.],
       			[0., 0., 0., 0.]])

7）使用empty_like创建形状相同的数组：empty_like(prototype, dtype=None)。

In [18]: np.empty_like(x)
Out[18]: array([          0,           0, -1391817984,         445, 
				-1391821424,    	 445, -1391821264,         445])
				
In [19]: np.empty_like(X)
Out[19]: array([[          0,           0, -1391820064,         445],
       			[-1391821264,         445, -1391817984,         445]])

8）使用full创建指定值的数组：np.full(shape, fill_value, dtype=None, order='C')。

In [20]: np.full(10, 666)
Out[20]: array([666, 666, 666, 666, 666, 666, 666, 666, 666, 666])

In [21]: np.full((2, 4), 333)
Out[21]: array([[333, 333, 333, 333],
       			[333, 333, 333, 333]])

9）使用full_like创建形状相同的数组：np.full_like(a, fill_value, dtype=None)。

In [22]: np.full_like(x, 666)
Out[22]: array([666, 666, 666, 666, 666, 666, 666, 666])

In [23]: np.full_like(X, 666)
Out[23]: array([[666, 666, 666, 666],
       			[666, 666, 666, 666]])

• 生成随机数的np.random模块构建。

使用random模块生成n维随机数的数组：randn(d0, d1, ..., dn)，传几个参数就是几维向量。

In [24]: np.random.randn()  # 返回一个随机值
Out[24]: 1.9203198746884742

In [25]: np.random.randn(3)  # 一维向量，3 个随机值
Out[25]: array([0.71853108, 0.45361075, 0.41838299])

In [26]: np.random.randn(3, 2) # 二维向量，3 行 2 列
Out[26]: array([[ 1.05735799,  0.82315323],
       			[-0.89745967, -0.72472225],
     			[-0.3110142 , -0.71354229]])

In [27]: np.random.randn(3, 2, 4)   # 三维向量类比成一本书，3 页 2 行 4 列
Out[27]: array([[[-0.34495803,  0.27231417,  1.2860603 ,  1.41123575],
        		 [-0.20243816, -0.59274924, -0.75639519, -0.14023731]],

       			[[-0.96726883,  0.10792837, -1.99454855, -1.55116908],
        		 [-0.51470216,  0.45716025,  0.9045223 , -0.84280536]],

       			[[ 0.38567078, -0.44643378, -0.27161385,  1.41790034],
        		 [ 0.23899078, -0.72325399, -0.66842487,  0.32939194]]])

3. array本身的属性：

• shape：返回一个元组，表示array的维度；
• ndim：一个数字，表示array的维度数目；
• size：一个数字，表示array中所有数据元素的数目；
• dtype：array中元素的数据类型。

这里的x和X是2中演示创建array的方法时，创建的变量。

In [28]: x.shape # 一维数组的shape，是一个元组，里面只有一个数，表示有8个数据
Out[28]: (8,)

In [29]: X.shape # 二维数组的shape，是一个元组，有两个数，会显示 2 行 4 列
Out[29]: (2, 4)

In [30]: x.ndim # 1 维
Out[30]: 1

In [31]: X.ndim # 2 维
Out[31]: 2

In [32]: x.size # 数组元素个数
Out[32]: 8

In [33]: x.dtype # 数组类型
Out[33]: dtype('int32')

In [34]: X.dtype
Out[34]: dtype('int32')

4. array本身支持大量的操作和函数

• 有直接逐元素的加减乘除等算数操作；
• 更好用的面向多维的数组索引；
• 求sum/mean等的聚合函数；
• 线性代数函数，比如求解逆矩阵、求解方程组。

这些操作如果用Python实现需要很多for循环，用numpy数组很容易实现：

In [35]: A = np.arange(10).reshape(2, 5)  # 把一维数组变成二维数组，这个数组是 2 行 5 列
		 A
Out[35]: array([[0, 1, 2, 3, 4],
       			[5, 6, 7, 8, 9]])

In [36]: A.shape # 查看 A 的维度
Out[36]: (2, 5)

In [37]: A+1 # 给每个元素都加一个 1
Out[37]: array([[ 1,  2,  3,  4,  5],
       			[ 6,  7,  8,  9, 10]])

In [38]: A*3 # 给每个元素都乘 3
Out[38]: array([[ 0,  3,  6,  9, 12],
       			[15, 18, 21, 24, 27]])

In [39]: np.sin(A) # 求每个数值对应的 sin 函数
Out[39]: array([[ 0.        ,  0.84147098,  0.90929743,  0.14112001, -0.7568025 ],
       			[-0.95892427, -0.2794155 ,  0.6569866 ,  0.98935825,  0.41211849]])

In [40]: np.exp(A) # e的x次方，x 就是每个数值
Out[40]: array([[1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
        		 5.45981500e+01],
       			[1.48413159e+02, 4.03428793e+02, 1.09663316e+03, 2.98095799e+03,
        		 8.10308393e+03]])

矩阵间的运算：

In [41]: B = np.random.randn(2, 5) # 先创建一个和 A 维度相同的数组
		 B
Out[41]: array([[-1.18121507,  0.14372464,  0.87297923,  0.36016626,  0.26290856],
       			[-1.98466356, -0.3558747 , -0.41947815, -0.06944038, -0.08719276]])

In [42]: A+B
Out[42]: array([[-1.18121507,  1.14372464,  2.87297923,  3.36016626,  4.26290856],
       			[ 3.01533644,  5.6441253 ,  6.58052185,  7.93055962,  8.91280724]])

In [43]: A-B
Out[43]: array([[1.18121507, 0.85627536, 1.12702077, 2.63983374, 3.73709144],
       			[6.98466356, 6.3558747 , 7.41947815, 8.06944038, 9.08719276]])

---

3. Numpy怎么对数组按照索引进行查询

---

初始化数组：

In [1]: import numpy as np

In [2]: # 一维向量
		x = np.arange(10)
		x
Out[2]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [3]: # 二维向量，一般用大写字母
		X = np.arange(20).reshape(4, 5)
		X
Out[3]: array([[ 0,  1,  2,  3,  4],
       		   [ 5,  6,  7,  8,  9],
       	 	   [10, 11, 12, 13, 14],
       		   [15, 16, 17, 18, 19]])

1. 基础索引

• 一维数组：

In [4]: x
Out[4]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [5]: print(x[2], x[5], x[-1]) # 使用下标来访问
Out[5]: 2 5 9

In [6]: # 使用切片访问，下标为 2 的位置开始到 4 位置结束，不包含 4
		x[2:4] 
Out[6]: array([2, 3])

In [7]: # 从 2 位置开始到最后一个，不包括最后一个
		x[2:-1]
Out[7]: array([2, 3, 4, 5, 6, 7, 8])

• 二维数组：

In [8]: X
Out[8]: array([[ 0,  1,  2,  3,  4],
       		   [ 5,  6,  7,  8,  9],
       		   [10, 11, 12, 13, 14],
       		   [15, 16, 17, 18, 19]])

In [9]: # 分别用行坐标、列坐标、实现行列筛选
		X[0, 0]
Out[9]: 0

In [10]: # 先选取最后一行，然后取其中的第二列
		 X[-1, 2]
Out[10]: 17

In [11]: # 可以省略后续索引值，返回的数据是降低一个维度的数组
		 # 下标为 2 的行
		 X[2]
Out[11]: array([10, 11, 12, 13, 14])

In [12]: # 筛选-1对应的行
		 X[-1]
Out[12]: array([15, 16, 17, 18, 19])

In [13]: # 筛选除了 -1 外的多行
		 # 相当于是仅对行进行了切片操作
		 X[:-1]
Out[13]: array([[ 0,  1,  2,  3,  4],
       			[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14]])

In [14]: # 筛选多行，然后筛选多列
	     X[:2, 2:4]
Out[14]: array([[2, 3],
       			[7, 8]])

In [15]: # 筛选所有行，然后取其中一列
		 X[:, 2] # 返回一维数组，相当于只取了其中一列
Out[15]: array([ 2,  7, 12, 17])

• 注意：Numpy中对切片修改会修改原来的数组，因为Numpy经常要处理大数组，避免每次都复制。

In [16]: x
Out[16]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [17]: x[2:4] = 666
		 x
Out[17]: array([  0,   1, 666, 666,   4,   5,   6,   7,   8,   9])

In [18]: X[:1, :2] = 666
		 X
Out[18]: array([[666, 666,   2,   3,   4],
       			[  5,   6,   7,   8,   9],
       			[ 10,  11,  12,  13,  14],
       			[ 15,  16,  17,  18,  19]])

2. 用整数数组进行索引

• 一维数组：

In [19]: # 一维数组
		 x = np.arange(10)
		 x
Out[19]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [20]: # 访问 3,4,7 位置对应的数据
		 x[[3, 4, 7]]
Out[20]: array([3, 4, 7])

In [21]: # 索引是二维的
		 indexs = np.array([[0, 2], [1, 3]])
		 x[indexs] # 返回一个二维数组
Out[21]: array([[0, 2],
       			[1, 3]])

实例：获取数组中最大的前n个数字。

In [22]: # 随机生成 1 到 100 之间的，10 个数字
		 arr = np.random.randint(1, 100, 10)
		 arr
Out[22]: array([80, 94, 75, 49, 83, 27, 52, 85, 71, 81])

In [23]: # arr.argsort() 
		 # 从小到大排序，不改变原数组，返回排序后的下标
		 arr.argsort()
Out[23]: array([5, 3, 6, 8, 2, 0, 9, 4, 7, 1], dtype=int64)

In [24]: # 取最大值对应的 3 个下标
		 arr.argsort()[-3:]
Out[24]: array([4, 7, 1], dtype=int64)

In [25]: arr[arr.argsort()[-3:]]
Out[25]: array([83, 85, 94])

• 二维数组：

In [26]: X = np.arange(20).reshape(4, 5)
		 X
Out[26]: array([[ 0,  1,  2,  3,  4],
       			[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14],
       			[15, 16, 17, 18, 19]])

In [27]: # 筛选多行，列可以省略
		 X[[0, 2]] # 只取第0行，和第2行
Out[27]: array([[ 0,  1,  2,  3,  4],
       			[10, 11, 12, 13, 14]])

In [28]: # 上面的代码相当于 : 省略
		 X[[0, 2], :]
Out[28]: array([[ 0,  1,  2,  3,  4],
       			[10, 11, 12, 13, 14]])

In [29]: # 筛选多行，行不能省略
		 X[:, [0, 2, 3]]
Out[29]: array([[ 0,  2,  3],
       			[ 5,  7,  8],
       			[10, 12, 13],
       			[15, 17, 18]])

In [30]: # 同时指定行列
		 # 这时实际上已经定位到了单个的元素，返回一维数组
		 X[[0, 2, 3], [1, 3, 4]]
Out[30]: array([ 1, 13, 19])

3. 布尔索引

• 一维数组：

In [31]: # 将数据还原
		 x = np.arange(10)
		 x
Out[31]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [32]: x>5 # 返回布尔值
Out[32]: array([False, False, False, False, False, False,  True,  True,  True,
        		True])

In [33]: x[x>5] # 筛选出 x 大于 5 的数
Out[33]: array([6, 7, 8, 9])

In [34]: # 实例：把一维数组进行01化处理
		 # 比如把房价数字，变成“高房价”为1，“低房价”为0
		 x[x<=5] = 0
		 x[x>5] = 1
		 x
Out[34]: array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1])

In [35]: x = np.arange(10)
		 x[x<5] += 20 # 把所有 < 5 的数都加上 20
		 x
Out[35]: array([20, 21, 22, 23, 24,  5,  6,  7,  8,  9])

• 二维数组：

In [36]: X = np.arange(20).reshape(4,5)
		 X
Out[36]: array([[ 0,  1,  2,  3,  4],
       			[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14],
       			[15, 16, 17, 18, 19]])

In [37]: X > 5
Out[37]: array([[False, False, False, False, False],
       			[False,  True,  True,  True,  True],
       			[ True,  True,  True,  True,  True],
       			[ True,  True,  True,  True,  True]])

In [38]: # X>5返回的boolean数组，其实既有行，又有列
		 # 因此返回的是一维结果
		 X[X>5]
Out[38]: array([ 6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19])

In [39]: X[:, 3] # 所有行，第三列对应的数字
Out[39]: array([ 3,  8, 13, 18])

In [40]: # 将第 3 列大于 5 的行筛选出来
		 X[:, 3]>5 # 这个boolean数组只有行
Out[40]: array([False,  True,  True,  True])

In [41]: # 将第 3 列数字大于 5 的所有行筛选出来
		 X[X[:, 3]>5]
Out[41]: array([[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14],
       			[15, 16, 17, 18, 19]])
In [42]: # 将第 3 列数值大于 5 的所有行，变成 666
		 X[X[:, 3]>5] = 666
		 X
Out[42]: array([[  0,   1,   2,   3,   4],
       			[666, 666, 666, 666, 666],
       			[666, 666, 666, 666, 666],
       			[666, 666, 666, 666, 666]])

• 条件的组合：

In [43]: x = np.arange(10)
		 x
Out[43]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [44]: # 注意，每个条件都要加小括号
		 condition = (x%2==0)|(x>7)
		 condition
Out[44]: array([ True, False,  True, False,  True, False,  True, False,  True,
        		 True])

In [45]: x[condition]
Out[45]: array([0, 2, 4, 6, 8, 9])

In [46]: X = np.arange(20).reshape(4, 5)
		 X
Out[46]: array([[ 0,  1,  2,  3,  4],
       			[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14],
       			[15, 16, 17, 18, 19]])

In [47]: condition = (X%2==0)|(X>7)
		 condition
Out[47]: array([[ True, False,  True, False,  True],
       			[False,  True, False,  True,  True],
       			[ True,  True,  True,  True,  True],
       			[ True,  True,  True,  True,  True]])

In [48]: X[condition]
Out[48]: array([ 0,  2,  4,  6,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19])

关于布尔索引大家可能会不太理解，为什么有时候对二维数组使用布尔索引，返回的是一位数组；而有时候，返回的是二维数组？

这里可以简单理解为，如果布尔索引的数组是二维的，则将这个布尔索引传给二维数组，是可以唯一确定行和列的，也就是说能精确的找到每一个元素，此时返回的就是一维数组。如果布尔索引是一维的，则这个布尔索引只能确定行号，传给二维数组就会返回一个二维数组，找到对应的行。

---

5. Numpy常用的random随机函数

---

官方的文档说明：https://docs.scipy.org/doc/numpy-1.14.0/reference/routines.random.html

函数名	说明
seed([seed])	设定随机种子，这样每次生成的随机数会相同
rand(d0, d1, …, dn)	返回数据在 [0, 1) 之间，具有均匀分布
randn(d0, d1, …, dn)	返回数据具有标准正态分布（均值为0，方差为1）
randint(low[ , high, size, dtype])	生成随机整数，包含low，不包含high
random([size])	生成 [0.0, 1.0) 的随机整数
choice(a[, size, replace, p])	a是一维数组，从它里面生成随机结果
shuffle(x)	把一个数组x进行随机排列
permutation(x)	把一个数组x进行随机排列，或者数字的全排列
normal([loc, scale,size])	按照平均值loc和方差scale生成高斯分布的数字
unform([low, high, size])	在[low, high)之间生成均匀分布的数字

导入Numpy，并设置随机数种子：

In [1]: import numpy as np
		np.random.seed(666)

1. rand(d0, d1, …, dn)，返回数据在 [0, 1) 之间，具有均匀分布：

In [2]: np.random.rand(5)
Out[2]: array([0.70043712, 0.84418664, 0.67651434, 0.72785806, 0.95145796])

In [3]: np.random.rand(3, 4) # 二维数组
Out[3]: array([[0.0127032 , 0.4135877 , 0.04881279, 0.09992856],
       		   [0.50806631, 0.20024754, 0.74415417, 0.192892  ],
               [0.70084475, 0.29322811, 0.77447945, 0.00510884]])
               
In [4]: np.random.rand(2, 3, 4) # 三维数组
Out[4]: array([[[0.11285765, 0.11095367, 0.24766823, 0.0232363 ],
        		[0.72732115, 0.34003494, 0.19750316, 0.90917959],
        		[0.97834699, 0.53280254, 0.25913185, 0.58381262]],

       		   [[0.32569065, 0.88889931, 0.62640453, 0.81887369],
        		[0.54734542, 0.41671201, 0.74304719, 0.36959638],
        		[0.07516654, 0.77519298, 0.21940924, 0.07934213]]])

2. randn(d0, d1, …, dn)，返回数据具有标准正态分布（均值为0，方差为1）：

In [5]: np.random.randn(5)
Out[5]: array([-1.20990266, -0.04618272, -0.44118244,  0.46953431,  0.44325817])

In [6]: np.random.randn(3, 4)
Out[6]: array([[-1.66738875, -1.81731749, -1.39753916,  0.78392691],
       		   [-0.29129965,  0.67049043,  0.706931  ,  1.42965241],
       		   [-0.41407013, -1.32672274, -0.14880188,  0.34771289]])
       		   
In [7]: np.random.randn(2, 3, 4)
Out[7]: array([[[ 0.61030791, -1.17532603,  0.82985368, -0.30236752],
        		[-0.04327047,  0.06706965, -1.59102817,  0.01705112],
        		[-1.87296591, -0.96457904, -0.00420389,  0.47495047]],

       		   [[-0.05421452,  0.89181355,  0.96866859,  0.6307865 ],
        		[-0.89051986,  0.08227022, -0.07594056,  0.42969347],
        		[ 0.11579967, -0.54443241,  0.02835341,  1.34408655]]])

3. randint(low[ , high, size, dtype])，生成随机整数，包含low，不包含high；若不指定high，则从[0, low)中生成数字：

In [8]: np.random.randint(3)
Out[8]: 2

In [9]: np.random.randint(1, 10) # 生成 1 到 10 之间的数
Out[9]: 1

In [10]: np.random.randint(10, 30, size=(5,)) # 指定 size 生成 5 个元素
Out[10]: array([27, 16, 25, 18, 18])

In [11]: np.random.randint(10, 30, size=(2, 3, 4)) # 2 页 3 行 4 列
Out[11]: array([[[26, 19, 14, 21],
        		 [29, 25, 19, 21],
        		 [28, 12, 13, 19]],

       			[[27, 27, 18, 27],
        		 [16, 24, 16, 19],
        		 [21, 20, 19, 14]]])

4. random([size])，生成 [0.0, 1.0) 的随机整数：

In [12]: np.random.random(5)
Out[12]: array([0.95858105, 0.66579831, 0.84015904, 0.14691185, 0.14394403])

In [13]: np.random.random(size=(3, 4))
Out[13]: array([[0.30843116, 0.37016398, 0.31852964, 0.56240025],
       			[0.4640979 , 0.80066784, 0.78735522, 0.84323067],
       			[0.68824287, 0.31854825, 0.93794112, 0.40711455]])

In [14]: np.random.random(size=(2, 3, 4))
Out[14]: array([[[0.75336448, 0.5065076 , 0.8242313 , 0.48603164],
        		 [0.17872445, 0.79322194, 0.13924006, 0.71347858],
        		 [0.38300909, 0.70410853, 0.82867258, 0.58154578]],

       			[[0.38693726, 0.39648041, 0.15039198, 0.08835265],
        		 [0.80002064, 0.86760024, 0.88654384, 0.76250128],
       			 [0.2158761 , 0.60311702, 0.17688438, 0.15759693]]])

5. choice(a[, size, replace, p])，如果a是一个数n，则从[0, n)之间生成随机数；如果a是一维数组，从数组里面挑数生成随机结果：

In [15]: # 这时 a 是数字，从rang(a)中生成随机数，size为 3
		 np.random.choice(5, 3)
Out[15]: array([4, 2, 4])

In [16]: np.random.choice(5, (2, 3)) # 生成二维数组
Out[16]: array([[3, 3, 2],
       			[4, 0, 2]])
In [17]: np.random.choice([2, 3, 6, 7, 9], 3)
Out[17]: array([3, 9, 6])

In [18]: np.random.choice([2, 3, 6, 7, 9], (2, 3))
Out[18]: array([[7, 9, 2],
       			[6, 9, 6]])

6. shuffle(x)，把一个数组x进行随机排列（将数据进行打散）：

In [19]: a = np.arange(10)
		 np.random.shuffle(a)
		 a
Out[19]: array([7, 2, 3, 6, 1, 9, 8, 4, 0, 5])

In [20]: a = np.arange(20).reshape(4, 5)
		 a
Out[20]: array([[ 0,  1,  2,  3,  4],
       			[ 5,  6,  7,  8,  9],
       			[10, 11, 12, 13, 14],
       			[15, 16, 17, 18, 19]])

In [21]: # 如果数据是多维的，则只会在第一维度打散数据
		 np.random.shuffle(a) # 打乱行
		 a # 直接修改了数组
Out[21]: array([[10, 11, 12, 13, 14],
       			[ 0,  1,  2,  3,  4],
      		    [15, 16, 17, 18, 19],
       			[ 5,  6,  7,  8,  9]])

7. permutation(x)，把一个数组x进行随机排列，或者数字的全排列：

In [22]: # 这时候，生成range(10)的随机排列
		 np.random.permutation(10)
Out[22]: array([1, 5, 3, 0, 2, 4, 7, 9, 6, 8])

In [23]: arr = np.arange(9).reshape((3, 3))
		 arr
Out[23]: array([[0, 1, 2],
       			[3, 4, 5],
       			[6, 7, 8]])

In [24]: # 在第一维度打散
		 # 注意：这里不会更改原来的 arr ，会返回一个新的拷贝
		 np.random.permutation(arr)
Out[24]: array([[6, 7, 8],
       			[3, 4, 5],
       			[0, 1, 2]])

In [25]: arr # 原数组不变
Out[25]: array([[0, 1, 2],
       			[3, 4, 5],
       			[6, 7, 8]])

8. normal([loc, scale,size])，按照平均值loc和方差scale生成高斯分布的数字：

In [26]: np.random.normal(1, 10, 10) # size 是一维的
Out[26]: array([ 10.80291099,  13.10516541, -23.0910327 ,  14.49409934,
        		 -6.290444  ,  -9.42735397,  -2.28926527, -13.71681338,
       			 -13.04515295,  -5.32726848])
In [27]: np.random.normal(1, 10, (3, 4)) # size 是二维的
Out[27]: array([[  3.00692005,   2.62218924,   2.60682046,  13.11370959],
       			[-12.63957919,   2.30310161,  13.59875359,  10.79500364],
       			[ 18.37674494, -13.17309889,  -3.82004022, -20.47660377]])

9. unform([low, high, size])，在[low, high)之间生成均匀分布的数字：

In [28]: np.random.uniform(1, 10, 10)
Out[28]: array([2.64932089, 4.78167451, 7.11195067, 3.90634783, 8.86690648,
       			8.48692156, 1.73313319, 6.41664569, 8.79063733, 7.4360877 ])

In [29]: np.random.uniform(1, 10, (3, 4))
Out[29]: array([[1.8056582 , 9.60886484, 1.08734758, 8.40955337],
       			[5.67535321, 2.0603951 , 5.7577428 , 7.03324951],
       			[3.101973  , 6.9400552 , 2.04862106, 4.44717637]])

实例：对数组加入随机噪声。

In [30]: import matplotlib.pyplot as plt

In [31]: # 绘制sin曲线
		 # 生成x轴
		 x = np.linspace(-10, 10, 100) # 指定最小数和最大数，在它们之间生成100个点
		 # 生成y轴
		 y = np.sin(x)
		 plt.plot(x, y) # 绘图
		 plt.show()

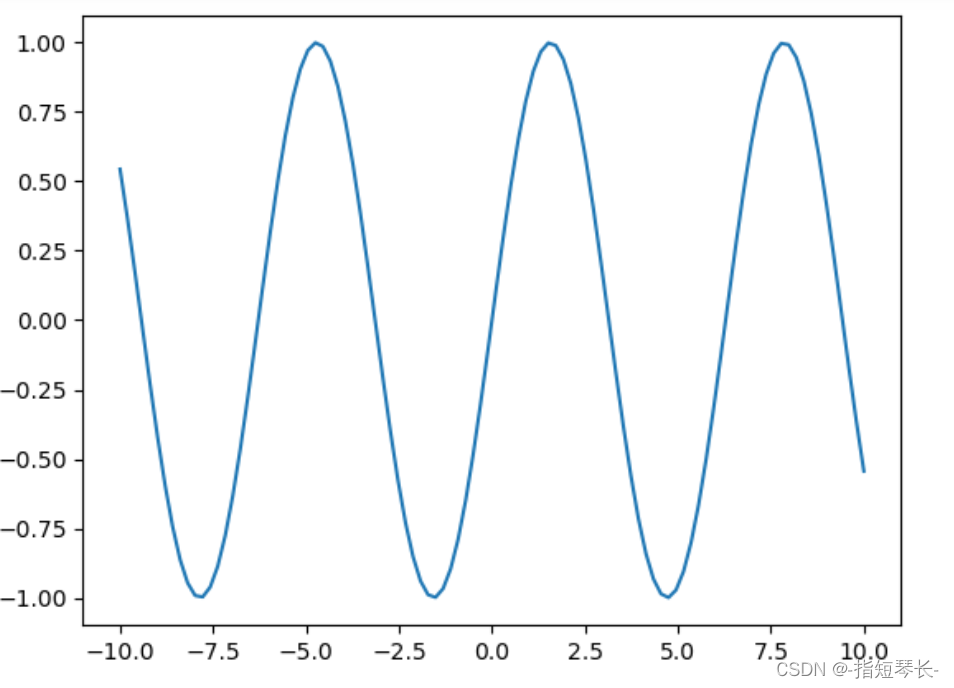
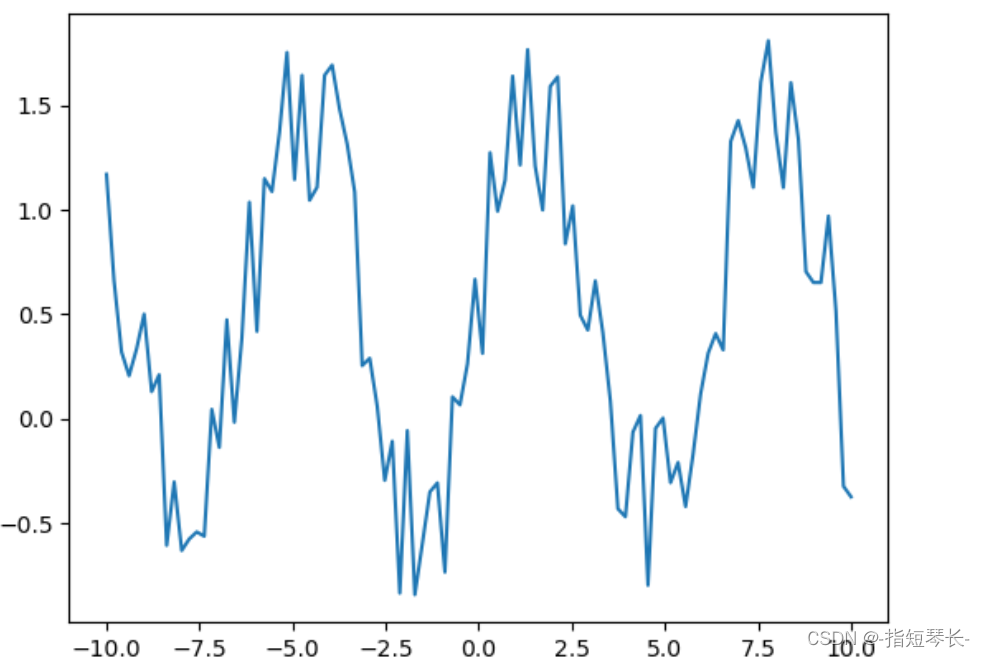
In [32]: # 加入噪声
		 x = np.linspace(-10, 10, 100)
		 y = np.sin(x) + np.random.rand(len(x)) # x参数是维度
		 plt.plot(x, y)
		 plt.show()

---

6. Numpy的数学统计函数

---

1. Numpy常用数学统计函数：

函数名	说明
np.sum	所有元素的和
np.prod	所有元素的乘积
np.cumsum	元素的累积加和
np.cumprod	元素的累积乘积
np.min	最小值
np.max	最大值
np.percentle	0-100百分位数
np.quantile	0-1分位数
np.median	中位数
np.average	加权平均，参数可以指定welghts
np.mean	平均值
np.std	标准差
np.var	方差

In [1]: import numpy as np

In [2]: arr = np.arange(12).reshape(3, 4)
		arr
Out[2]: array([[ 0,  1,  2,  3],
       		   [ 4,  5,  6,  7],
       		   [ 8,  9, 10, 11]])

In [3]: np.sum(arr) # 所有元素的和
Out[3]: 66

In [4]: np.prod(arr) # 所有元素的乘积
Out[4]: 0

In [5]: np.cumsum(arr) # 累积加和
Out[5]: array([ 0,  1,  3,  6, 10, 15, 21, 28, 36, 45, 55, 66])

In [6]: np.cumprod(arr) # 累积乘积
Out[6]: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

In [7]: np.min(arr)
Out[7]: 0

In [8]: np.max(arr)
Out[8]: 11

In [9]: # 先对序列从小到大排序，取 25% 50% 75% 对应位置的数据
		np.percentile(arr,[25, 50, 75])
		# 如果序列是偶数，则中位数，50% 位置对应的数是不存在的，它等于旁边两个数相加 /2
Out[9]: array([2.75, 5.5 , 8.25])

In [10]: # 和上面 percentile 的运行结果是一样的
		 np.quantile(arr, [0.25, 0.5, 0.75])
Out[10]: array([2.75, 5.5 , 8.25])

In [11]: np.median(arr) # 中位数
Out[11]: 5.5

In [12]: np.std(arr) # 标准差
Out[12]: 3.452052529534663

In [13]: np.var(arr) # 方差
Out[13]: 11.916666666666666

In [14]: # weights 的 shape 需要和 arr 一样
		 weights = np.random.rand(*arr.shape)
		 np.average(arr, weights=weights) # 加权平均
Out[14]: 5.615811474229254

2. 按照不同的axis（轴）计算：

以上函数都有一个参数叫axis用于指定计算轴为行还是列，如果不指定，那么会计算所有元素的结果。

axis=0 代表行，axis=1 代表列。对于sum/mean/media等聚合函数：axis=0 代表把所有行压扁，合成一行；axis=1 代表把所有列压扁，合成一列。

In [15]: arr
Out[15]: array([[ 0,  1,  2,  3],
       			[ 4,  5,  6,  7],
       			[ 8,  9, 10, 11]])

In [16]: # 行压扁，对应位置数据相加
		 arr.sum(axis=0)
Out[16]: array([12, 15, 18, 21])

In [17]: # 列压扁，对应位置数据相加
		 arr.sum(axis=1)
Out[17]: array([ 6, 22, 38])

In [18]: # 行压扁，对应位置数据累加求和
		 arr.cumsum(axis=0)
Out[18]: array([[ 0,  1,  2,  3],
       			[ 4,  6,  8, 10],
       			[12, 15, 18, 21]])

In [19]: # 列压扁，对应位置数据累加求和
		 arr.cumsum(axis=1)
Out[19]: array([[ 0,  1,  3,  6],
       			[ 4,  9, 15, 22],
       			[ 8, 17, 27, 38]])

3. 实例：机器学习中将数据进行标准化。

In [20]: arr
Out[20]: array([[ 0,  1,  2,  3],
       			[ 4,  5,  6,  7],
       			[ 8,  9, 10, 11]])

arr对应到现实世界中的一种解释是：

• 行：每行对应一个样本数据。
• 列：每列代表样本的一个特征。

数据标准化：

• 对于机器学习，神经网络来说，不同列的量纲应该相同，训练收敛的更快；
• 比如商品的价格是0到100元，销量是1万个到10万个，这两个数字没有可比性，因此需要做标准化处理；
• 不同列代表不同的特征，因此需要axis=0做计算；
• 标准化一般使用A = (A - mean(A, axis=0)) / std(A, axis=0)公式进行计算。

In [21]: # 计算每列的均值
		 mean = np.mean(arr, axis=0)
		 mean
Out[21]: array([4., 5., 6., 7.])

In [22]: # 计算每列的标准差
		 std = np.std(arr, axis=0)
		 std
Out[22]: array([3.26598632, 3.26598632, 3.26598632, 3.26598632])

In [23]: # 计算分子
		 # 此时 mean 是一维数组，令 arr - mean 会让 arr 的每一行都减去 mean，称为 numpy 广播
		 A = arr - mean
		 A
Out[23]: array([[-4., -4., -4., -4.],
       			[ 0.,  0.,  0.,  0.],
       			[ 4.,  4.,  4.,  4.]])

In [24]: result = A/std
		 result
Out[24]: array([[-1.22474487, -1.22474487, -1.22474487, -1.22474487],
       		 	[ 0.        ,  0.        ,  0.        ,  0.        ],
       			[ 1.22474487,  1.22474487,  1.22474487,  1.22474487]])

上面示例中arr的分布太均匀了，现实中不会有这么均匀的数据，接下来我们用随机数再试一次：

In [25]: arr2 = np.random.randint(1, 100, size=(3, 4))
		 arr2
Out[25]: array([[72, 12, 58, 11],
       			[97,  9, 79, 68],
       			[22, 29, 35, 29]])

In [26]: result = (arr2 - np.mean(arr2, axis=0)) / np.std(arr2, axis=0)
		 result
Out[26]: array([[ 0.26726124, -0.52990781,  0.03710071, -1.05082838],
       			[ 1.06904497, -0.87056284,  1.20577299,  1.34506033],
       			[-1.33630621,  1.40047065, -1.2428737 , -0.29423195]])

---

7. Numpy计算数组中满足条件元素的个数

---

需求：有一个非常大的数组比如1亿个数字，求出里面数字大于5000的数字数目。

1. 使用numpy的random模块生成1亿个数字：

In [1]: import numpy as np

In [2]: arr = np.random.randint(1, 10000, size=int(1e8))

In [3]: arr[:10]
Out[3]: array([6746, 5571, 3192, 7390, 8094, 8740, 6406,  867, 9961, 5842])

In [4]: arr.size
Out[4]: 100000000

2. 使用Python原生语法实现上述需求：

In [5]: pyarr = list(arr) # 转成Python中的list

In [6]: # 计算结果
		len([x for x in pyarr if x>5000])
Out[6]: 49987308

In [7]: # 记下时间
		%timeit len([x for x in pyarr if x>5000])
Out[7]: 7.14 s ± 158 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

3. 使用Numpy实现：

In [8]: arr[arr>5000].size
Out[8]: 49987308

In [9]: (arr>5000)[:10]
Out[9]: array([ True,  True, False,  True,  True,  True,  True, False,  True,
        		True])

In [10]: # 记下时间
		 %timeit arr[arr>5000].size
Out[10]: 545 ms ± 8.09 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

4. 对比时间：

In [11]: # 对比时间
		 (7.14 * 1000)/545
Out[11]: 13.100917431192661

Numpy比Python的原生语法快了13倍左右。

---

8. Numpy怎样给数组增加一个维度（转置）

---

背景：

很多数据计算都是二维或三维的，对于一维的数据输入，为了形状匹配，经常需升维变成二维。

需求：

在不改变数据的情况下，添加数组维度。

• 原始数组：一维数组arr=[1, 2, 3, 4]，其shape是(4, )，取值分别为arr[0], arr[1], arr[2], arr[3]；
• 变形数组：二维数组arr=[[1, 2, 3, 4]]，其shape是(1, 4)，取值分别为a[0, 0], a[0, 1], a[0, 2], a[0, 3]。

3种方法：

• np.newaxis：关键字，使用索引的语法给数组添加维度；
• np.expand_dims(arr, axis)：方法，和np.newaxis实现一样的功能，给arr在axis位置添加维度；
• np.reshape(a, newshape)：方法，给一个维度设置为1完成升维。

实操：

初始化数组

In [1]: import numpy as np

In [2]: arr = np.arange(5)
		arr
Out[2]: array([0, 1, 2, 3, 4])

In [3]: # 当前是一维向量
		arr.shape
Out[3]: (5,)

1） np.newaxis：关键字，使用索引的语法给数组添加维度；

注意：np.newaxis其实就是None的别名。即以下所有的np.newaxis都可以用None来代替。

In [4]: np.newaxis is None
Out[4]: True

In [5]: np.newaxis == None
Out[5]: True

给一维向量添加一个行维度。

In [6]: arr[np.newaxis, :]
Out[6]: array([[0, 1, 2, 3, 4]])

In [7]: # 数据现在是 1 行 5 列
		arr[np.newaxis, :].shape
Out[7]: (1, 5)

给一维向量添加一个列维度（转置）。

In [8]: arr[:, np.newaxis]
Out[8]: array([[0],
       		   [1],
       		   [2],
       		   [3],
       		   [4]])

In [9]: arr[:, np.newaxis].shape
Out[9]: (5, 1)

2）np.expand_dims(arr, axis)：方法，和np.newaxis实现一样的功能，给arr在axis位置添加维度；

np.expand_dims方法实现的效果，和np.newaxis关键字是一模一样的。

In [10]: arr
Out[10]: array([0, 1, 2, 3, 4])

In [11]: np.expand_dims(arr, axis=0) # 相当于 arr[None, arr]
Out[11]: array([[0, 1, 2, 3, 4]])

In [12]: np.expand_dims(arr, axis=1) # 相当于 arr[arr, None]
Out[12]: array([[0],
       			[1],
       			[2],
       			[3],
       			[4]])

3）np.reshape(a, newshape)：方法，给一个维度设置为1完成升维。

In [13]: arr
Out[13]: array([0, 1, 2, 3, 4])

In [14]: np.reshape(arr, (1, 5))
Out[14]: array([[0, 1, 2, 3, 4]])

In [15]: # 很多情况下我们不知道具体要传多少列，可以传 -1，numpy会自己计算应该会有多少列
		 np.reshape(arr, (1, -1))
Out[15]: array([[0, 1, 2, 3, 4]])

In [16]: np.reshape(arr, (-1, 1)) # 自动计算仅 1 列的情况下有多少行
Out[16]: array([[0],
       			[1],
       			[2],
       			[3],
       			[4]])

---

9. Numpy非常重要的数据合并操作

---

背景： 在给机器学习准备数据的过程中，经常需要进行不同来源的数据合并操作。

两类场景：

• 给已有数据添加多行，比如添加一些样本数据进去；
• 给已有数据添加多列，比如添加一些特征进去。

以下操作均可以实现数组合并：

• np.concatenate(array_list, axis=0/1)：沿着指定axis进行数组的合并；
• np.vstack或者np.row_stack(array_list)：沿着vertically、按照row wise进行数据合并（按行进行数据合并）；
• np.hstack或者np.column_stack(array_list)：水平horizontally、按照column wise进行数据合并（按列进行数据合并）。

初始化数据：

In [1]: import numpy as np

In [2]: a = np.arange(6).reshape(2, 3)
		b = np.random.randint(10, 20, size=(4, 3))

In [3]: a
Out[3]: array([[0, 1, 2],
       		   [3, 4, 5]])

In [4]: b
Out[4]: array([[18, 12, 13],
       		   [11, 11, 12],
       		   [17, 13, 11],
       	 	   [14, 15, 10]])

1）给数据添加多行：

In [5]: np.concatenate([a, b]) # 把 b 拼到 a 的后面，axis默认是 0，所以这里不用传
Out[5]: array([[ 0,  1,  2],
       		   [ 3,  4,  5],
       		   [18, 12, 13],
       		   [11, 11, 12],
       		   [17, 13, 11],
               [14, 15, 10]])

In [6]: np.vstack([a, b])
Out[6]: array([[ 0,  1,  2],
       		   [ 3,  4,  5],
       		   [18, 12, 13],
       		   [11, 11, 12],
       		   [17, 13, 11],
       		   [14, 15, 10]])

In [7]: np.row_stack([a, b])
Out[7]: array([[ 0,  1,  2],
       		   [ 3,  4,  5],
       		   [18, 12, 13],
       		   [11, 11, 12],
       		   [17, 13, 11],
       		   [14, 15, 10]])

2）给数据添加多列：

In [8]: a = np.arange(12).reshape(3, 4)
		b = np.random.randint(10, 20, size=(3, 2))

In [9]: a
Out[9]: array([[ 0,  1,  2,  3],
       		   [ 4,  5,  6,  7],
       		   [ 8,  9, 10, 11]])

In [10]: b
Out[10]: array([[13, 17],
       			[15, 11],
       			[17, 13]])

In [11]: np.concatenate([a, b], axis=1)
Out[11]: array([[ 0,  1,  2,  3, 13, 17],
       			[ 4,  5,  6,  7, 15, 11],
       			[ 8,  9, 10, 11, 17, 13]])

In [12]: np.hstack([a, b])
Out[12]: array([[ 0,  1,  2,  3, 13, 17],
       			[ 4,  5,  6,  7, 15, 11],
       			[ 8,  9, 10, 11, 17, 13]])

In [13]: np.column_stack([a, b])
Out[13]: array([[ 0,  1,  2,  3, 13, 17],
       			[ 4,  5,  6,  7, 15, 11],
       			[ 8,  9, 10, 11, 17, 13]])

---

10. Numpy的文件操作

---

10.1 从文件中读取array

---

我们的很多数据都是存储在文件中的，所以Numpy也设计了如何从文件中读取数据的方法。下面我们来实现一个需求，从文件中读取一个二维数组。

1. 初始化文件：

In [1]: import numpy as np

In [2]: %%writefile tang.txt
		0 1 2 3 4
		5 6 7 8 9
Out[2]: Writing tang.txt

2. 打开对应目录，查看文件：

3. 用Python原生语法实现从文件中读取这段数据：

In [3]: data = []
		with open('tang.txt') as f:
    		for line in f:
        		fileds = line.split()
        		cur_data = [float(x) for x in fileds]
        		data.append(cur_data)
		data = np.array(data) # 转成 numpy 中的 array

In [4]: data
Out[4]: array([[0., 1., 2., 3., 4.],
       		   [5., 6., 7., 8., 9.]])

4. 用Numpy实现：

In [5]: data = np.loadtxt('tang.txt')
		data
Out[5]: array([[0., 1., 2., 3., 4.],
       	 	   [5., 6., 7., 8., 9.]])

• 如果分隔符是,呢？

In [6]: %%writefile tang.txt
		0,1,2,3,4
		5,6,7,8,9
Out[6]: Overwriting tang.txt

In [7]: data = np.loadtxt('tang.txt', delimiter = ',') # 指定分隔符
		data
Out[7]: array([[0., 1., 2., 3., 4.],
       		   [5., 6., 7., 8., 9.]])

• 如果第一行是无效数据呢？

In [8]: %%writefile tang.txt
		x,y,z,w,a
		0,1,2,3,4
		5,6,7,8,9
Out[8]: Overwriting tang.txt

In [9]: data = np.loadtxt('tang.txt', delimiter = ',', skiprows = 1) # skiprows 指定跳过几行
		data
Out[9]: array([[0., 1., 2., 3., 4.],
       		   [5., 6., 7., 8., 9.]])
       		   
In [10]: data = np.loadtxt('tang.txt', delimiter = ',', skiprows = 2) # skiprows 指定跳过几行
		 data
Out[10]: array([5., 6., 7., 8., 9.])

• 如果想筛选出对应的列呢？

In [11]:  # 选出第 0 2 4 列
		 data = np.loadtxt('tang.txt', delimiter=',', skiprows = 1, usecols = (0, 2, 4))
		 data
Out[11]: array([[0., 2.],
       			[5., 7.]])

5. 总结：

• 'tang.txt'：文件路径；
• skipprows: 去掉几行；
• delimiter：分隔符；
• usecols：指定使用哪几列；

---

10.2 向文件中写入array

---

在机器学习的过程中，我们有时希望，可以临时保存一下数据，这又该怎么实现呢？

1. 初始化数组：

In [12]: tang_array = np.array([[1, 2, 3],[4, 5, 6]])
		 tang_array
Out[12]: array([[1, 2, 3],
       			[4, 5, 6]])

2. 向文件中写入数组：

In [13]: np.savetxt('tang.txt', tang_array)

默认分割符是空格。

3. 打开文件查看内容：

发现数据很复杂，是用科学计数法来存储的，我们来简化一下。

4. 控制写入格式：

In [14]: np.savetxt('tang.txt', tang_array, fmt='%d') # 以整数形式写入

顺便把控制分隔符也说一下：

In [15]: np.savetxt('tang.txt', tang_array, fmt='%f', delimiter=',')

5. 保存多个数组：

实际上，我们不喜欢用txt文档来存储数组信息，更常用的文件格式是npy格式。

In [16]: tang_array = np.array([[1, 2, 3],[4, 5, 6]])
		 np.save('tang_array.npy', tang_array) # 文件后缀为 npy

这里.npy文件不好查看，我就不再打开看了。

In [17]: tang = np.load('tang_array.npy')
		 tang
Out[17]: array([[1, 2, 3],
       			[4, 5, 6]])

保存多个数组。

In [18]: tang_array2 = np.arange(10).reshape(2,5)
		 tang_array2
Out[18]: array([[0, 1, 2, 3, 4],
       			[5, 6, 7, 8, 9]])

In [19]: # 保存为.npz格式
		 np.savez('tang.npz', a=tang_array, b=tang_array2)

In [20]: data = np.load('tang.npz')

In [21]: data['a']
Out[21]: array([[1, 2, 3],
       			[4, 5, 6]])

In [22]: data['b']
Out[22]: array([[0, 1, 2, 3, 4],
       			[5, 6, 7, 8, 9]])

.npz文件实际上就是一个压缩文件，里面有多个.npy文件，每个.npy文件对应一个数据。

---