探索拉普拉斯算子：计算机视觉中用于边缘检测和图像分析的关键工具

一、介绍

????????拉普拉斯算子是 n 维欧几里得空间中的二阶微分算子，表示为 ?2。它是函数梯度的发散度。在图像处理的上下文中，该运算符应用于图像的强度函数，可以将其视为每个像素具有强度值的二维信号。拉普拉斯算子是计算机视觉领域的关键工具，广泛用于各种用途，如边缘检测、图像锐化和图像空间结构分析。本文深入探讨了拉普拉斯算子的概念、其数学基础、在计算机视觉中的应用及其一些局限性。

通过拉普拉斯的镜头，每个像素都揭示了对比和轮廓的故事，解锁了数字领域中隐藏的图像语言。

二、数学背景

定义

在数学上，函数 f（x， y） 的拉普拉斯量定义为：

这表示函数相对于每个空间维度的二阶偏导数之和。

三、离散近似

????????在数字图像中，我们处理离散值，因此连续拉普拉斯量使用有限差分进行近似。这通常采用应用于图像的卷积核或掩码的形式。

3.1 在计算机视觉中的应用

1. 边缘检测：?拉普拉斯算子在计算机视觉中的主要应用之一是边缘检测。图像中的边缘是具有高强度对比度的区域，对于理解图像中物体的结构至关重要。拉普拉斯算子突出显示了强度快速变化的区域，这些区域通常与边缘相关联。
2. 图像锐化：?拉普拉斯也可用于增强图像中的细节。通过从原始图像中减去拉普拉斯，可以强调边缘，从而产生锐化效果。
3. 斑点检测：?在斑点检测中，拉普拉斯算子有助于识别图像中强度变化显著的区域。这在对象识别和场景分析等任务中特别有用。

3.2 高斯拉普拉斯 （LoG）

????????高斯拉普拉斯算子 （LoG） 是高斯平滑和拉普拉斯算子应用的组合。这种方法有助于在边缘检测之前降低噪声，使过程更加稳健。

3.3 局限性

1. 对噪声敏感：拉普拉斯算子对噪声高度敏感。在实际应用中，在应用拉普拉斯滤波器之前，通常需要使用高斯滤波器对图像进行平滑处理，以最大程度地减少噪声的影响。
2. 规模依赖关系：拉普拉斯算子的有效性与尺度有关。它可能无法有效地检测与正在使用的拉普拉斯核的比例不匹配的边缘或特征。

四、代码

????????创建一个完整的 Python 代码示例来演示在计算机视觉中使用拉普拉斯算子需要几个步骤。我们将创建一个合成数据集（简单图像），应用拉普拉斯算子，然后绘制结果。此示例将使用 NumPy 等库进行数值运算，并使用 Matplotlib 进行绘图。

????????首先，确保您安装了必要的库。您可以使用 pip 安装它们：

pip install numpy matplotlib opencv-python

import numpy as np
import cv2
import matplotlib.pyplot as plt

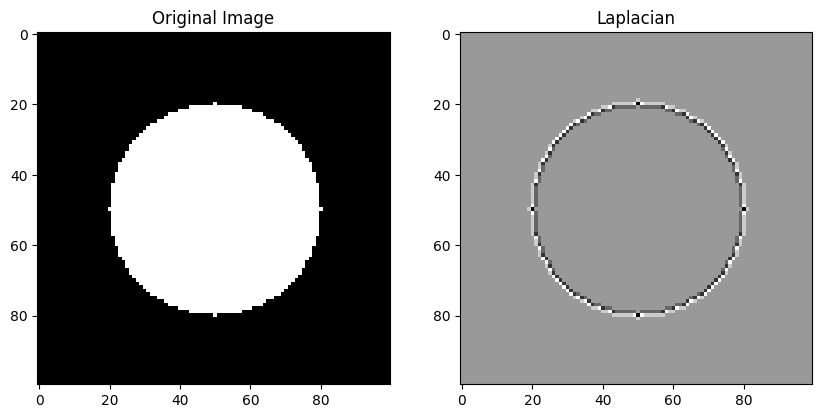
# Step 1: Create synthetic images
def create_synthetic_image(shape, object_type):
    image = np.zeros(shape, dtype=np.uint8)
    if object_type == 'circle':
        cv2.circle(image, (shape[1] // 2, shape[0] // 2), 30, (255, 255, 255), -1)
    elif object_type == 'square':
        cv2.rectangle(image, (shape[1] // 4, shape[0] // 4), (3 * shape[1] // 4, 3 * shape[0] // 4), (255, 255, 255), -1)
    return image

# Step 2: Apply the Laplacian operator
def apply_laplacian(image):
    return cv2.Laplacian(image, cv2.CV_64F)

# Step 3: Plotting the results
def plot_results(original, laplacian):
    plt.figure(figsize=(10, 5))

    plt.subplot(1, 2, 1)
    plt.imshow(original, cmap='gray')
    plt.title('Original Image')

    plt.subplot(1, 2, 2)
    plt.imshow(laplacian, cmap='gray')
    plt.title('Laplacian')

    plt.show()

# Create a synthetic image and apply Laplacian
synthetic_image = create_synthetic_image((100, 100), 'circle')
laplacian_image = apply_laplacian(synthetic_image)

# Plotting
plot_results(synthetic_image, laplacian_image)

运行代码

运行此脚本将创建一个合成图像，应用拉普拉斯运算符，并显示原始图像和处理后的图像。您可以尝试不同的形状或更复杂的合成图像，以了解拉普拉斯算子对不同空间结构的反应。请记住，拉普拉斯算子对噪声很敏感，因此在实际应用中，通常需要高斯平滑等预处理步骤。

五、结论

????????拉普拉斯算子是计算机视觉领域的基础工具，具有从边缘检测到图像增强的广泛应用。虽然它有局限性，特别是在对噪声的敏感性方面，但它在突出图像中重要空间特征方面的实用性使其成为计算机视觉工具包中不可或缺的一部分。图像处理领域先进技术和算法的持续发展继续利用拉普拉斯算子的核心原理，证明了其在该领域的持久相关性。