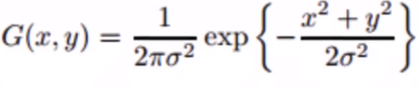基于Matlab的各种图像滤波Filter算法（代码开源）

发布时间：2024年01月01日

前言：本文为手把手教学 Matlab 平台下的各种图像滤波算法的教程，将编程代码与图像滤波知识相联系，以实战为例！博客中图像滤波算法包含：均值滤波、中值滤波、高斯滤波、双边滤波、引导滤波。图像滤波算法是计算机视觉领域CV必修课，被广泛运用于各行各业，尤其是科研领域！希望本篇博客能给读者朋友的工程项目或科研生活给予些许帮助。（篇末代码开源！）

图像滤波算法总图：

一、图像滤波知识

1.1 基本概念

图像滤波是一种常见的图像处理技术，旨在抑制图像中的噪声，并在尽量保留图像细节特征的条件下改善图像质量。该技术是图像预处理中非常重要的步骤，将直接影响后续的图像数据挖掘与分析性能（例如：目标检测，目标分割与去雾去雨算法等）！其实如今大火的卷积神经网络 CNN 其实也是滤波的一种，都是用卷积核去提取图像的特征模式。不过传统的滤波，使用的卷积核是固定的参数，是由经验丰富的人去手动设计的，也称为手工特征。而卷积神经网络的卷积核参数是未知的，是根据不同的任务由数据驱动去学习得到的参数，更能适应于不同的任务。作者补充：卷积是图像算法中很重要的知识点，读者朋友一定需要熟练掌握!

1.2 图像噪声

在数字图像处理中，由于成像系统、传输介质和记录设备等的不完善，数字图像在其形成、传输和记录过程中往往会受到多种噪声的污染。这些噪声在图像上常表现为一些孤立像素点或像素块，它们以无用的信息形式出现，扰乱了图像的可观测信息。因此，图像滤波核心目的是消除这些噪声，以便更好地提取出图像的特征。

★常见的图像噪声分类：（1）椒盐噪声；（2）高斯噪声；（3）泊松噪声

1.2.1 椒盐噪声

椒盐噪声(salt-and-pepper noise)又称脉冲噪声，它随机改变一些像素值，在二值图像上表现为使一些像素点变白，一些像素点变黑。是由图像传感器，传输信道，解码处理等产生的黑白相间的亮暗点噪声，也就是老人们比较熟悉的所谓“雪花”。作者补充：RGB图像上的椒盐噪声也可以为红绿蓝（RGB）的像素点。

matlab代码：

%%椒盐噪声
close all;
clear all;
clc;
I=imread('test.png');
I=im2double(I);
% J = imnoise(I,‘salt & pepper’,d),默认d=0.05
% 在添加类型为Salt & Pepper的噪声时,符号&的前面和后面必须有空格,否则系统会出错
J=imnoise(I,'salt & pepper',0.01);
K=imnoise(I,'salt & pepper',0.05);
% 图像中黑色的像素点为椒盐噪声,白色的像素点为盐噪声
subplot(131),imshow(I);
subplot(132),imshow(J);
subplot(133),imshow(K);

1.2.2 高斯噪声

高斯噪声是一种源于电子电路噪声和由低照明度或高温带来的传感器噪声。高斯噪声又称为正态噪声，是自然界中最常见的噪声。高斯噪声可以通过平滑滤波技术或图像复原技术来消除。

matlab代码：

%%高斯滤波
close all;
clear all;
clc;
I=imread('test1.jpg');
h=0:0.1:1; % h为在[0,1]之间的向量,表示图像的亮度值
v=0.01:-0.001:0; % v为一个长度和h相同,表示与h中亮度对应的高斯噪声的方差
% J=imnoise(I,'localvar',h,v)在图像的不同亮度值上叠加不同方差的高斯噪声,向量h中没有的亮度值将自动插值得到
J=imnoise(I,'localvar',h,v);
subplot(121),imshow(I);
subplot(122),imshow(J);

1.2.3 泊松噪声

泊松噪声则是满足泊松分布的噪音，你会觉得它和正态分布很相似，其实如果我们采集的数据越多，精度越密，其形态上它越发接近高斯分布函数，也就是正态分布，是常见的一种满足指数函数分布的离散模型。

作者补充：噪声的添加效果一定程度上依赖初始图像，泊松噪声和高斯噪声看似一模一样，其实还是有些区别的。椒盐噪声和高斯噪声（指数型噪声）存在明显的区别，特别有随机性的感觉。读者朋友可以使用自己的图像进行测试，好好熟悉一下这些噪声！

matlab代码：

%%泊松噪声
close all;
clear all;
clc;
I=imread('test3.png');
% J = imnoise(I,‘poisson’)添加泊松噪声给图像I
J=imnoise(I,'poisson');
subplot(121),imshow(I);
subplot(122),imshow(J);

1.3 图像滤波分类

常见的线性滤波器：?
（1）低通滤波器：允许低频率通过；
（2）高通滤波器：允许高频率通过；?
（3）带通滤波器：允许一定区域的频率通过；
（4）带阻滤波器：阻止一定范围内的频率并且允许其他频率通过；
（5）全通滤波器：允许所有频率通过，仅仅改变相位；
（6）陷波滤波器 Band stop filter：阻止一个狭窄频率范围通过的特殊带阻滤波器。

★根据数学性质，图像滤波算法通常分为：线性滤波与非线性滤波

均值滤波–>? ? ? ? Blur函数 –> ? ? ? ? ? ? ? ? ? ? ? ?线性滤波?
高斯滤波–> ? ? ? ?GaussianBlur函数 –>? ? ? ? ?线性滤波?
中值滤波–> ? ? ? ?MedianBlur函数 –> ? ? ? ? ? ?非线性滤波?
双边滤波–> ? ? ? ?BilateralFilter函数 –> ? ? ? ? 非线性滤波
引导滤波–>? ? ? ? GuideFilter函数 –>? ? ? ? ? ? 非线性滤波

1.4 线性滤波原理

图像线性滤波原理：每个像素的输出值是输入像素的加权和。即利用给定像素周围的像素值的决定此像素的最终输出值的一种算子，本质上就是卷积核的使用！！！卷积就是图像处理中平滑（smoothing）/模糊（bluring）最大的幕后BOSS！

假设有 7x7 的图像像素点矩阵。卷积滤波过程：7x7 上面是个3x3的窗口，从左向右，从上向下移动，将图像中像素点与滤波窗口中的数据进行卷积计算得到数据作为新的像素点值保留。每次移动一个像素格（滤波窗口与步伐可以自己设定）。

二、均值滤波

2.1 算法概述

均值滤波是最简单的平滑滤波，通常图片中一个方块区域（一般为 3*3）内，中心点的像素为全部点像素值的平均值。均值滤波就是对于整张图片进行以上操作。

取卷积核（Kernel）区域下所有像素的平均值并替换中心元素，如下公式：

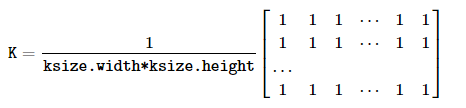
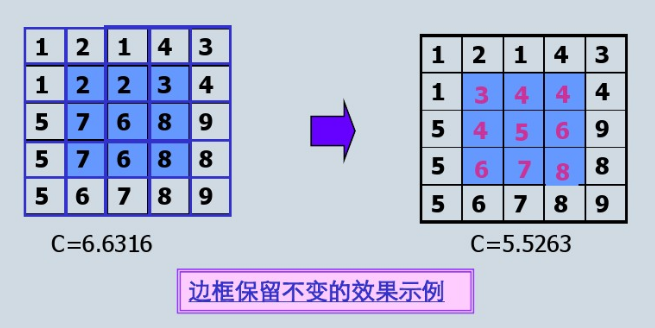
均值滤波算法案例图：

2.2 代码与分析

matlab代码：

%%均值滤波 
close all;
clear all;
clc;
I = imread('Noise Image.jpg');  % 读取图像 
%I = rgb2gray(I);  % 转换为灰度图像（如果需要）  
% 定义均值滤波器  
h = ones(3,3) / 9;  % 3x3的均值滤波器   
J = imfilter(I, h);  % 应用滤波器   
% 显示原始图像和滤波后的图像  
subplot(1,2,1), imshow(I), title('初始图像');  
subplot(1,2,2), imshow(J), title('均值滤波后的图像');

均值滤波图：

优点：均值滤波算法简单，计算速度快，算法容易实现。

缺点：由于均值滤波是通过对邻域像素的平均值来替代中心像素的值，因此容易导致图像细节的丢失；均值滤波会平滑图像中的高频部分，包括边缘和细节，使得图像边缘变得模糊。

三、中值滤波

3.1?算法概述

中值滤波是一种非线性信号处理技术，它将像素邻域内的所有像素值进行排序，并将中值作为输出。中值滤波对去除椒盐噪声特别有效。

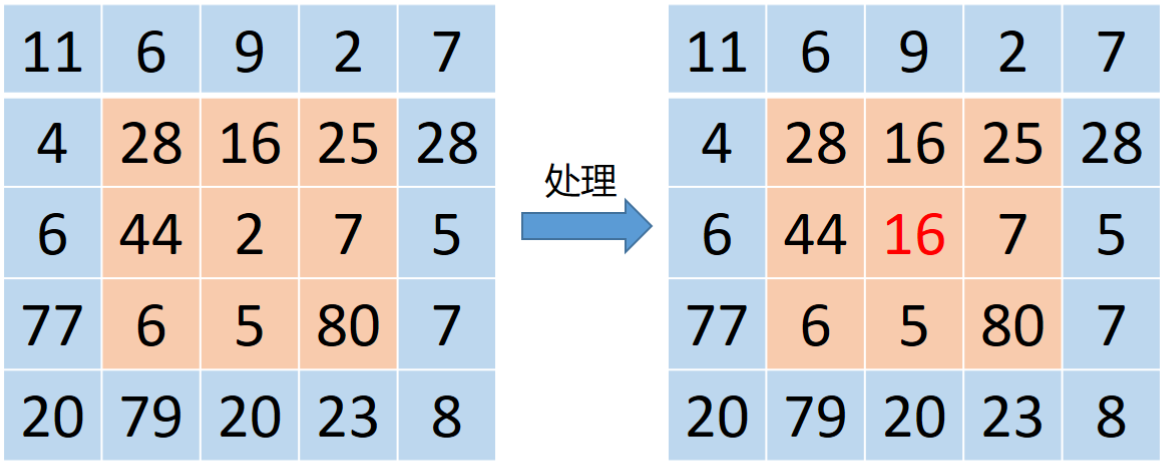
3.2?代码与分析

matlab代码：

%%中值滤波
close all;
clear all;
clc;
I = imread('Noise Image.jpg');  % 读取图像  
I = rgb2gray(I);  %转换为灰度图像（如果需要）  
J = medfilt2(I);  % 使用2D中值滤波器  % 应用中值滤波    
% 显示原始图像和中值滤波后的图像
subplot(1,2,1), imshow(I), title('原始图像');  
subplot(1,2,2), imshow(J), title('中值滤波后的图像');

中值滤波图：

优点：中值滤波可以有效地去除图像中的椒盐噪声、加性高斯噪声等噪声类型，使图像更清晰；相比其他滤波方法，中值滤波能够在去噪的同时较好地保留图像的边缘信息；中值滤波的计算过程也是简单容易的。

缺点：对于图像中含有较多点、线、尖角细节的情况，中值滤波可能不适用，因为它可能会改变这些细节的像素值；中值滤波是一种非线性滤波方法，它通过将像素邻域内的所有像素值排序来选择中值，这可能导致图像的不连续性。

四、高斯滤波

4.1?算法概述

高斯滤波(Gaussian filter) 包含许多种，包括低通、带通和高通等，我们通常图像上说的高斯滤波，指的是高斯模糊(Gaussian Blur) ，是一种高斯低通滤波，其过滤调图像高频成分（图像细节部分），保留图像低频成分（图像平滑区域），所以对图像进行 ‘高斯模糊’ 后，图像会变得模糊。高斯模糊对于抑制高斯噪声 (服从正态分布的噪声) 非常有效。

★高斯滤波和均值滤波一样，都是利用一个滤波窗口和图像进行卷积求解，不同之处在于：

均值滤波器的滤波窗口系数都是相同的，为1。
而高斯滤波器的滤波窗口系数，随着距离模板中心距离的增大，系数减小（服从二维高斯分布）。

高斯函数分布：

公式：

分布：高斯分布（正态分布）

?正态分布（高斯分布）是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。计算平滑结果时，只需要将"中心点"作为原点，其他点按照其在正态曲线上的位置，分配权重，就可以得到一个加权平均值。?

4.2?代码与分析

matlab代码：

%%高斯滤波
close all;
clear all;
clc; 
I = imread('Noise Image.jpg');  % 读取图像   
%I = rgb2gray(I);  % 转换为灰度图像（如果需要）    
J = imgaussfilt(I, 2);  % 使用标准差为2的高斯滤波器  % 应用高斯滤波器    
% 显示原始图像和高斯滤波后的图像  
subplot(1,2,1), imshow(I), title('原始图像');  
subplot(1,2,2), imshow(J), title('高斯滤波后的图像');

高斯滤波图：

优点：高斯滤波能够平滑图像，去除噪声，并保留图像的整体结构；高斯滤波可以通过调整高斯核的标准差来控制，灵活度高；高斯滤波在离散化窗口滑窗卷积实现时计算速度快，适用于实时处理。

缺点：高斯滤波器会平滑图像中的高频部分，包括边缘和细节，可能导致图像边缘模糊；高斯滤波需要进行卷积运算，计算复杂度相对较高，可能会消耗大量的计算资源和时间。

五、双边滤波

5.1?算法概述

双边滤波由 C. Tomasi 在1998 年提出，是一种经典的非线性空间滤波方法。在滤波器稀疏的制定上，双边滤波同时考虑到了输出像素与邻域内其它像素的欧氏距离和取值的差异，即：同时考虑到了空间域和值域间的差别。

（1）空间域核

由像素位置欧式距离决定的模板权值 $\omega _{d}$ ?。

为模板窗口的其他系数的坐标；

为模板窗口的中心坐标点；

$\sigma _{d}$ 是空间域上的高斯核函数的标准差，用于控制像素位置的权值。

使用公式生成的滤波器模板和高斯滤波器使用的模板是没有区别的。权值称为定义域核，也称为空间系数、空间域。显示由的计算公式可知，它是计算临近点q到中心点p临近程度，因此定义域核是用于衡量空间临近的程度。

（2）值域核?

由像素值的差值决定的模板权值 $\omega _{r}$ ?。

其中， $q(i,j)$ 为模板窗口的其他系数的坐标， $f(i,j)$ ?表示图像在点 $q(i,j)$ 处的像素值；

$p(k,l)$ 为模板窗口的中心坐标点，对应的像素值为 $f(k,l)$ ；

$\sigma _{r}$ 是像素值域上的高斯核函数的标准差，用于控制像素值的权值。

一般会将权值 $\omega _{r}$ 称为值域核，或像素值域，但不管是值域核 $\omega _{r}$ 还是空间域核 $\omega _{d}$ ，其大小都在[0 1]之间。

最后，将上述两个模板相乘就得到了双边滤波器的滑窗权值：

因此，双边滤波器的数据公式可以表示如下：

双边滤波器中的一边即为上述的高斯平滑滤波，两个像素物理距离越大则权值越小，反之则权值越大;双边滤波器中另一边由像素值值域决定，两个像素，灰度值相差越小，越不可能是边缘，那么越应该对其进行平滑处理，也就是应该提高其在滤波器中的权值,反之，像素值相差越大则越有可能是边缘，则应该尽力保留。

双边滤波的过程如下图，在突变的边缘上，使用了像素差权重，所以很好的保留了边缘：

5.2?代码与分析

matlab代码：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%彩色图双边滤波%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function g = bfilt_rgb(f,r,a,b)
% f灰度图；r滤波半径；a全局方差；b局部方差
[x,y] = meshgrid(-r:r);
w1 = exp(-(x.^2+y.^2)/(2*a^2));
f = tofloat(f);%f = im2double(f);
 
h = waitbar(0,'Applying bilateral filter...');
set(h,'Name','Bilateral Filter Progress');
 
fr = f(:,:,1);
fg = f(:,:,2);
fb = f(:,:,3);
[m,n] = size(fr);
fr_temp = padarray(fr,[r r],'symmetric');
fg_temp = padarray(fg,[r r],'symmetric');
fb_temp = padarray(fb,[r r],'symmetric');
[gr,gg,gb] = deal(zeros(size(fr)));
 
 
for i = r+1:m+r
    for j = r+1:n+r
        temp1 = fr_temp(i-r:i+r,j-r:j+r);
        temp2 = fg_temp(i-r:i+r,j-r:j+r);
        temp3 = fb_temp(i-r:i+r,j-r:j+r);
        dr = temp1 - fr_temp(i,j);
        dg = temp2 - fg_temp(i,j);
        db = temp3 - fb_temp(i,j);
        w2 = exp(-(dr.^2+dg.^2+db.^2)/(2*b^2));
        w = w1.*w2;
        gr(i-r,j-r) = sum(sum(temp1.*w))/sum(w(:));
        gg(i-r,j-r) = sum(sum(temp2.*w))/sum(w(:));
        gb(i-r,j-r) = sum(sum(temp3.*w))/sum(w(:));
    end
    waitbar((i-r)/n);
end
g = cat(3,gr,gg,gb);
% g = revertclass(g);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%可以用到的函数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [out,revertclass]=tofloat(in)
identity=@(x) x;
tosingle=@im2single;
 
table={'uint8',tosingle,@im2uint8
'uint16',tosingle,@im2uint16
'int16',tosingle,@im2int16
'logical',tosingle,@logical
'double',identity,identity
'single',identity,identity};
 
classIndex=find(strcmp(class(in),table(:,1)));
 
if isempty(classIndex)
    error('unsupported input immage class.');
end
 
out=table{classIndex,2}(in);
revertclass=table{classIndex,3};
end

%%双边滤波
close all;
clear all;
clc; 
I = imread('Noise Image.jpg');  % 读取图像   
%I = rgb2gray(I);  % 转换为灰度图像（如果需要）   
J = bfilt_rgb(I, 3, 9, 15);  % 9x9滤波器，空间标准差为15，灰度标准差为15  % 应用双边滤波器    
% 显示原始图像和双边滤波后的图像  
subplot(1,2,1), imshow(I);  
subplot(1,2,2), imshow(J);

双边滤波图：

优点：双边滤波能够同时考虑空间邻域和灰度值差异，因此在平滑图像的同时较好地保留边缘信息；双边滤波能够有效地去除图像中的噪声，特别是椒盐噪声；双边滤波的参数可调，可以根据不同的应用场景调整参数以获得最佳效果。

缺点：双边滤波需要进行卷积运算和排序操作，计算复杂度，会消耗非常多的计算成本；双边滤波的参数选择对滤波效果有很大影响，需要仔细调整以获得最佳效果。

六、引导滤波

6.1?算法概述

引导滤波的过程如下图所示，其在保边性能与计算复杂度上都达到了极优：?

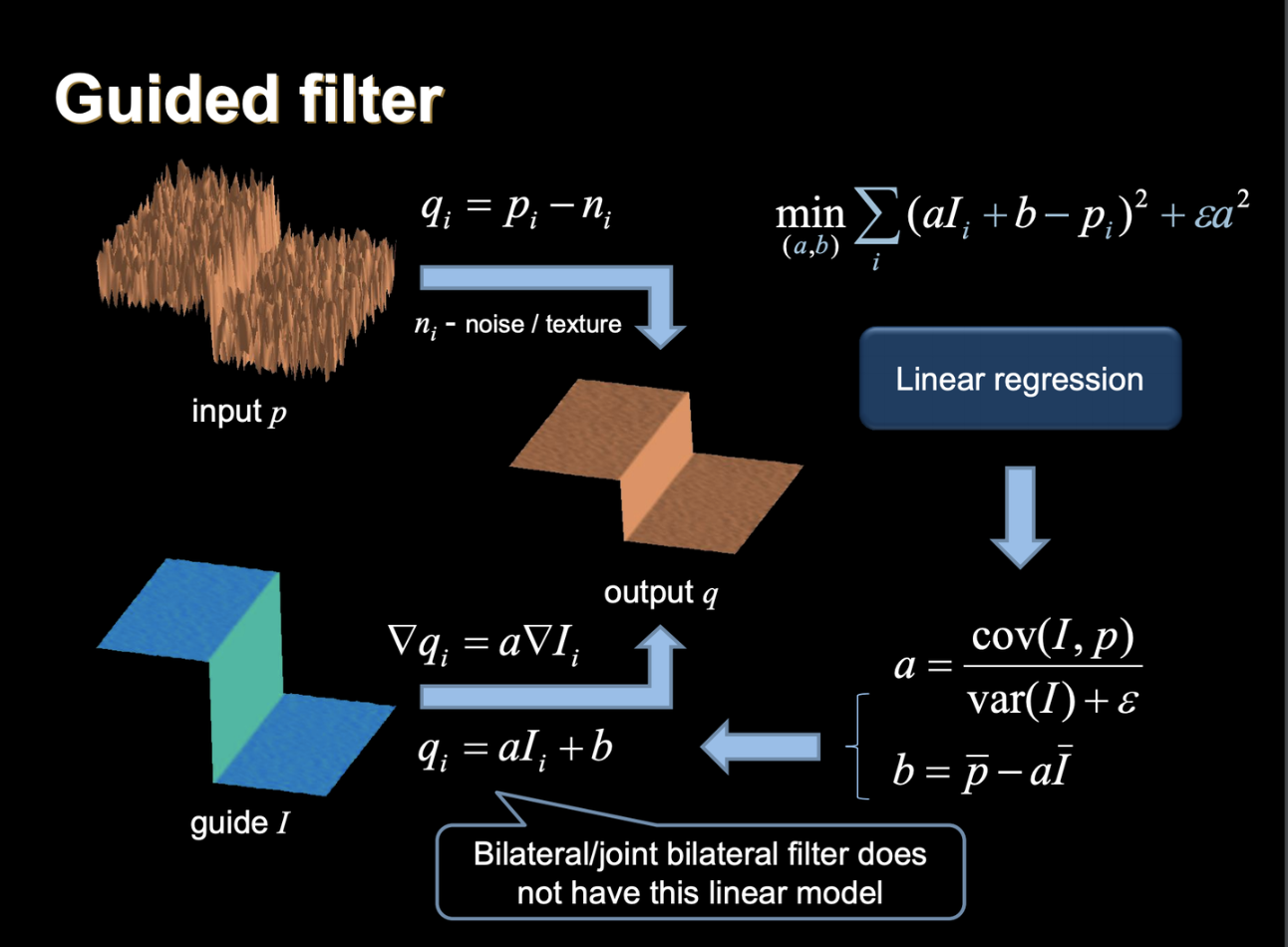
6.2?代码与分析

matlab代码：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function q = guidedfilter(I, p, r, eps)
%   GUIDEDFILTER   O(1) time implementation of guided filter.
%
%   - guidance image: I (should be a gray-scale/single channel image)
%   - filtering input image: p (should be a gray-scale/single channel image)
%   - local window radius: r
%   - regularization parameter: eps

[hei, wid] = size(I);
N = boxfilter(ones(hei, wid), r); % the size of each local patch; N=(2r+1)^2 except for boundary pixels.

mean_I = boxfilter(I, r) ./ N;
mean_p = boxfilter(p, r) ./ N;
mean_Ip = boxfilter(I.*p, r) ./ N;
cov_Ip = mean_Ip - mean_I .* mean_p; % this is the covariance of (I, p) in each local patch.

mean_II = boxfilter(I.*I, r) ./ N;
var_I = mean_II - mean_I .* mean_I;

a = cov_Ip ./ (var_I + eps); % Eqn. (5) in the paper;
b = mean_p - a .* mean_I; % Eqn. (6) in the paper;

mean_a = boxfilter(a, r) ./ N;
mean_b = boxfilter(b, r) ./ N;

q = mean_a .* I + mean_b; % Eqn. (8) in the paper;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function imDst = boxfilter(imSrc, r)

%   BOXFILTER   O(1) time box filtering using cumulative sum
%
%   - Definition imDst(x, y)=sum(sum(imSrc(x-r:x+r,y-r:y+r)));
%   - Running time independent of r; 
%   - Equivalent to the function: colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
%   - But much faster.

[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));

%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);

%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);
end

%%灰度图引导滤波
close all;
clear all;
clc; 
I = imread('Noise Image.jpg');  % 读取图像
if length(size(I))>2
    I=rgb2gray(I);
end
I = double(I) / 255;
p = I;
r = 9; 
eps = 0.4^2;      %0.021^2  0.04^2
J = guidedfilter(I,p,r,eps);           %引导滤波
% 显示原始图像和双边滤波后的图像  
subplot(1,2,1), imshow(I);  
subplot(1,2,2), imshow(J);

引导滤波图：

优点：引导滤波能够利用引导图像中的边缘信息，使输出图像的边缘与引导图像相似，因此在平滑图像的同时较好地保留边缘信息；由于引导滤波利用了引导图像的信息，因此对噪声具有一定的鲁棒性。

缺点：引导滤波需要进行卷积运算和迭代优化，可能会消耗很多的计算资源和时间（比双边滤波消耗时间短）；如果输入图像中存在大范围的噪声，引导滤波的效果可能会受到影响。

七、算法总结

图像滤波算法是计算机视觉领域必须掌握的技能，从事算法科研亦或是嵌入式AI行业的工程人员都应该熟练掌握它！图像滤波算法随着时代科学的进步，如今出现了许多新型的图像滤波算法，例如：反盲卷积滤波，侧窗盒式滤波与维纳滤波等。希望读者朋友在实际的工程项目中，不要盲目的追求各种牛逼的图像滤波算法，其实适合该工程的滤波就是好滤波！

八、代码开源

代码地址：?基于Matlab的各种图像滤波算法代码资源-CSDN文库

如果积分不够的朋友，点波关注，评论区留下邮箱，作者无偿提供源码和后续问题解答。求求啦关注一波吧?！！！

文章来源:https://blog.csdn.net/black_sneak/article/details/134427624
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！