飞行器Nz与Ny公式推导

发布时间：2024年01月03日

原始公式来源《飞行控制系统-吴森堂》

一：\beta、r推导ny

mV\dot{\beta }=-Tcos\alpha sin\beta +Y-mV(-psin\alpha +rcos\alpha ))+Gya? ? ? ? （式2-42）

\alpha \beta角度不大的情况下，可认为cos\alpha =1,sin\alpha =0,cos\beta =1,sin\beta =0

因此，式2-42化简可得：mV\dot{\beta }=Y-mVr+Gya

即mV\dot{\beta }+mVr=Y+Gya

mV\dot{\beta }+mVr=Y+Gya

\frac{V\dot{\beta }+Vr}{g}=\frac{Y+Gya}{mg}

\frac{V}{g}(\dot{\beta }+r)=\frac{Y+Gya}{mg}

增量方程：\frac{V}{g}(\Delta \dot{\beta }+\Delta r)=\Delta ny

二、\alpha q推导nz

mVcos\beta \dot{\alpha}=-Tsin\alpha-L+mV(-pcos\alpha sin\beta +qcos\beta -rsin\alpha sin\beta)+Gza（式2-42）

同理：\alpha \beta角度不大的情况下，可认为cos\alpha =1,sin\alpha =0,cos\beta =1,sin\beta =0

因此，可化简为：mV\dot{\alpha}=-L+mVq+Gza

L-Gza=mVq-mV\dot{\alpha}

\frac{L-Gza}{mg}=\frac{V}{g}(q-\dot{\alpha})

\frac{L}{mg}-1=nz-1=\frac{V}{g}(q-\dot{\alpha})

增量方程：\Delta nz=\frac{V}{g}(\Delta q-\Delta \dot{\alpha})

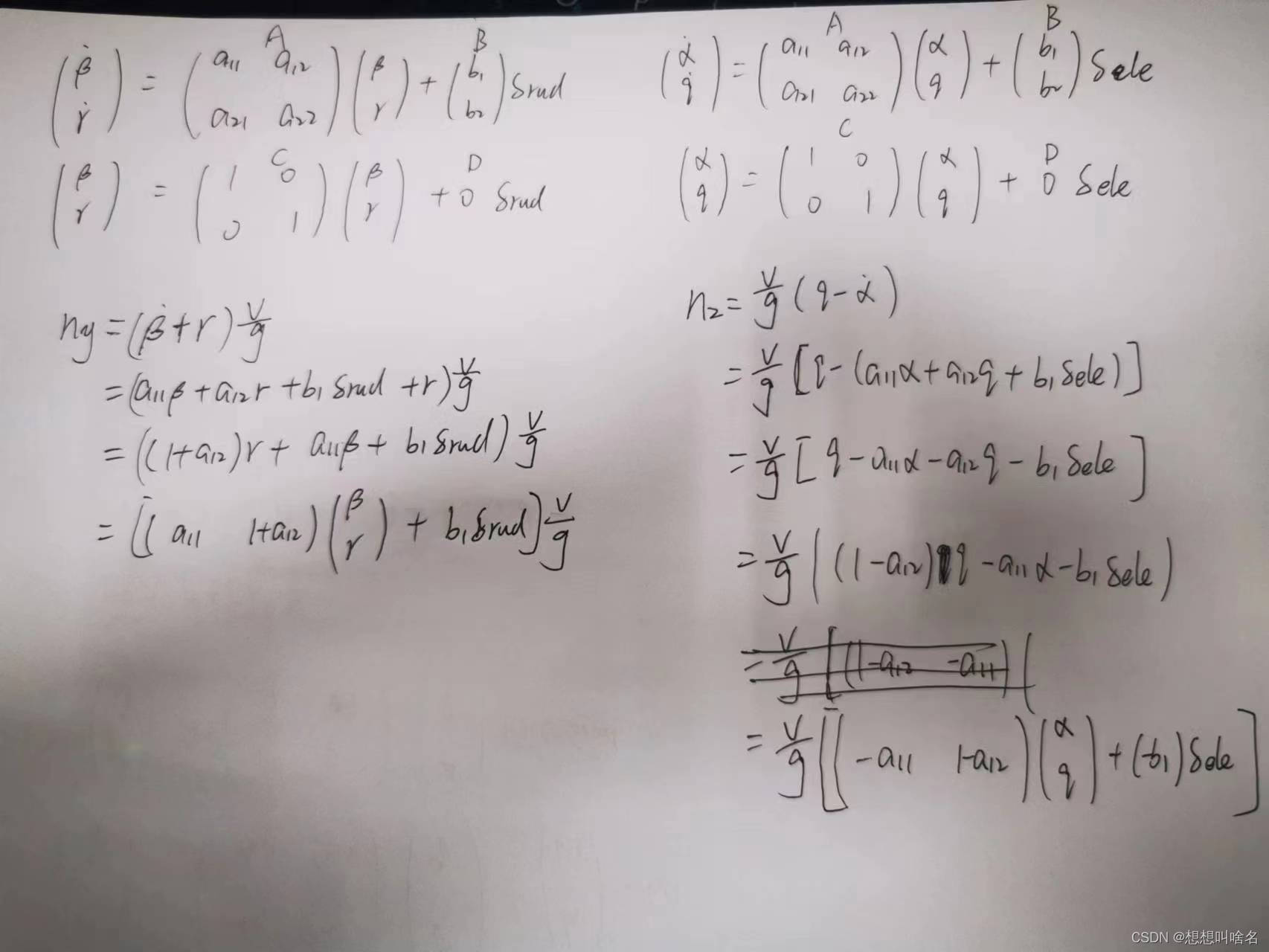
文章来源:https://blog.csdn.net/qq_35239859/article/details/135363497
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章