红黑树模拟实现
一,红黑树简介
1,红黑树的特点
首先我们得知道红黑树是什么才能知道这棵树里面应该有啥,红黑树其实有以下几个特点:
1,红黑树的每个节点是黑色或者红色的。
2,红黑树的根节点是黑色的。
3,红黑树不能出现两个连续的红节点。
4,红黑树的最长路径的长度不超过最短路径的长度的两倍。
5,红黑树的叶子节点是黑色的(这里的叶子节点指的是最后面的空节点)。
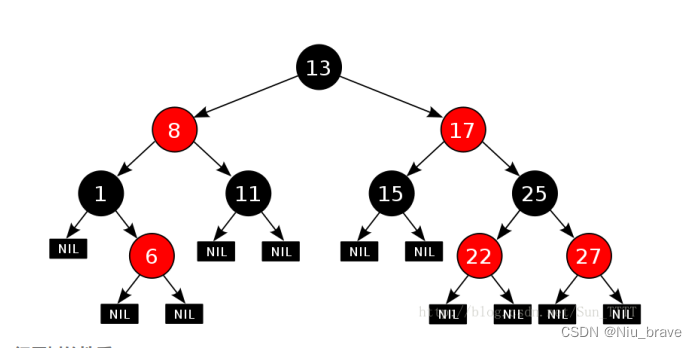
如下便是一棵红黑树:这里的规则五指的叶子节点便是最后的NIL节点。
2,红黑树的节点
? ? ? ? 在知道了红黑树的特点以后,便可以来讲讲红黑树节点的节点该如何构建了。按照上图红黑树节点成员有以下几个:
1,_left指针? 。??
?2,_right指针? 。??
3,_parent指针(主要是为了构建三叉戟方便找到父节点)。
4,表示颜色的变量(enum colour,枚举类型的colour)。
5,表示节点值的变量_val。
在知道上面的节点成员以后便可以开始构建节点了,构建出来的节点如下:
enum Colour //枚举类型的颜色。 {RED,BLACK}; template<class K,class V> struct RBNode { RBNode(const pair<K,V>&val)//为了后面插入值做准备。 :_val(val) ,_colour(RED)//一般插入的节点默认都是红色节点 {} //成员 pair<K, V>_val; RBNode<K, V>* _right; RBNode<K, V>* _left; RBNode<K, V>* parent; Colour _colour; };
?3,红黑树的插入
? ? ?红黑树归根结底还是一棵搜索二叉树,所以红黑树还是要符合搜索二叉树大的在右,小的在左的特点。所以红黑树的插入部分在前面还是和二叉·搜索树前面是一样的:
typedef RBNode<K, V> Node; bool Insert(const pair<K, V>& kv) { if (_root == nullptr)//当根节点为NULL时,要让他变成一个节点 { _root = new Node(val); _root->_colour = BLACK;//根节点为黑色 return true; } Node cur = _root; Node parent = nullptr; while (cur) { if (kv->first <cur._kv->first ) { parent = cur; cur = cur->_left } else if (kv->first > cur._kv->first) { parent = cur; cur = cur->_right; } else//插入一个已经存在的值 { return false; } } //cur走到空,parent时cur的上一个节点 //生成一个cur节点 cur = new Node(kv); //判断应该在parent的左边还是右边 if (cur._kv->first < parent._kv->first) { parent->_left = cur; } else { parent->_right = cur; } //挂好节点,以上的操作便是和二叉搜索树一样的操作 }然后便是不一样的,独属于红黑树的调整操作了。首先要明确一个点,红黑树在啥时候要调整呢?当然是在出现两个连续红色节点的情况下。
调整的方式有两种:1,直接变色。
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 2,旋转+变色。
并且旋转+变色的情况又分为四种:左,右,左右,右左。然后变色。(其实旋转的目的就是为了将下面四种情况转化为第一种情况来变色)。
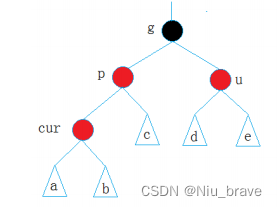
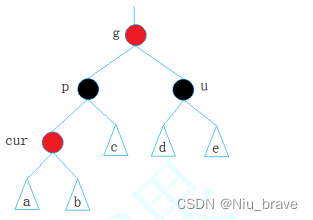
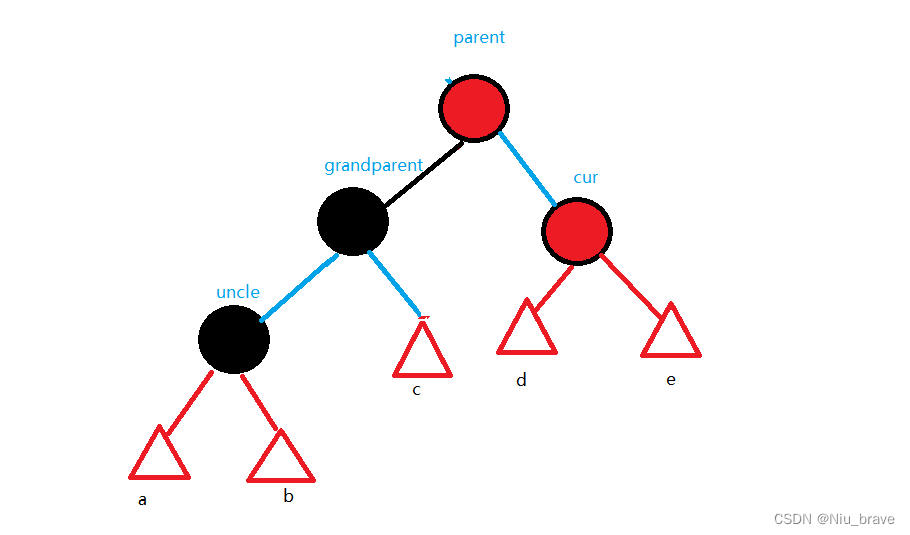
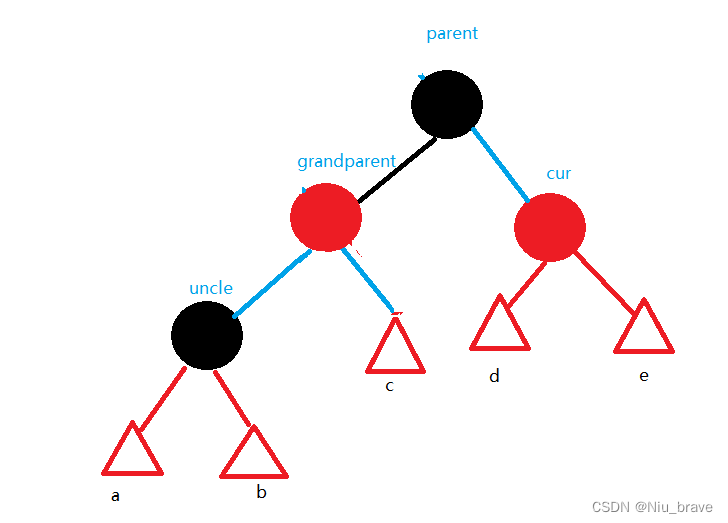
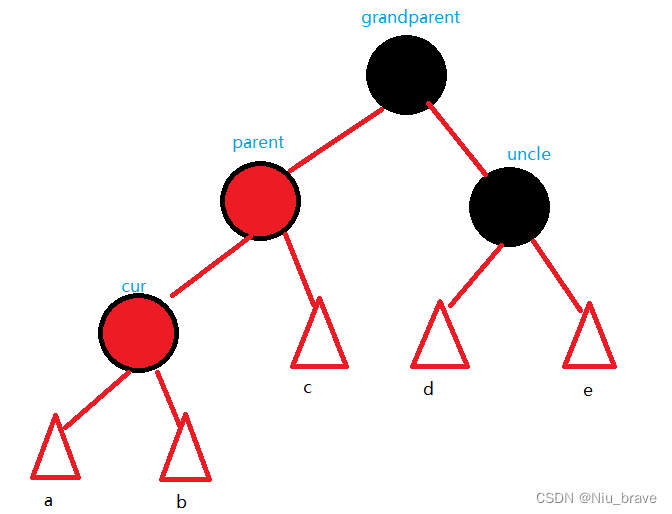
在调整之前,我们来将这些情况的总体示意图画出如下,并将几个关键节点(grandparent,parent,uncle,cur)画图如下:
到时候判断如何调整便要看这些节点的关系。现在来讨论五种情况:
1,变色
只变色的情况如下:1,parent为red,? ? 2,uncle为red。
示意图如下:
此时只需要变色,变色步骤如下:g变红,p和u变黑。
代码操作如下:
if (uncle->_colour == RED)//只变色 { grandparent->_colour = RED; uncle->_colour = BLACK; parent->_colour = BLACK; //向上调整,因为grandparent节点的颜色原来为BLACK,现在改为RED。可能会发生冲突情况,所以要向上调整。 cur = grandparent; parent = cur->_parent; }2,旋转加变色
旋转+变色的情况分为四种
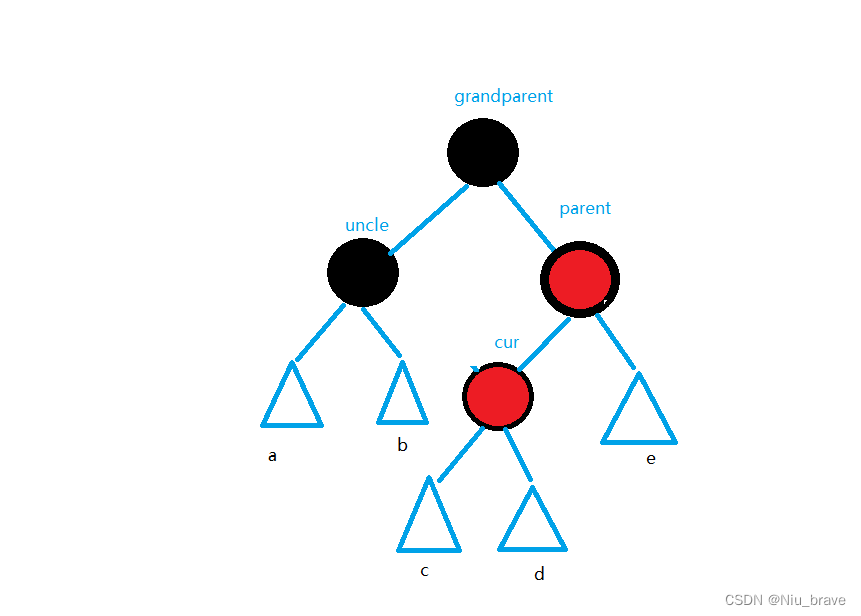
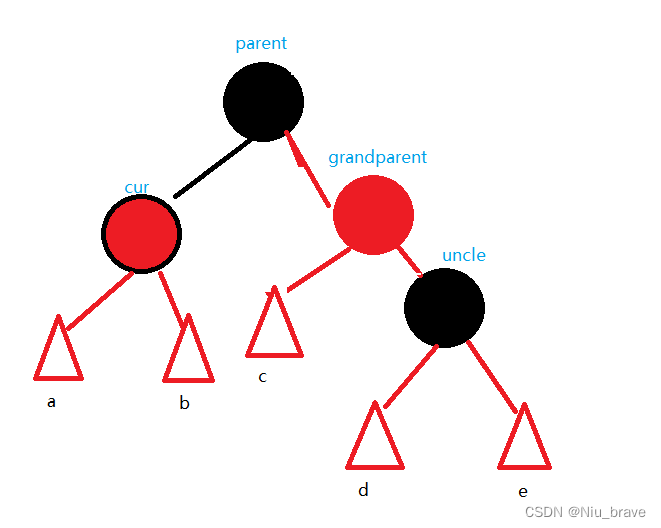
1.左+变色
要发生这个情况的调整的情况如下:
1.parent是grandparent的右边,并且cur是parent的右边。
示意图如下:
在这种情况下便要发生以grandparent为中心的左旋:
然后再将cur变为黑色。如下:
代码如下:
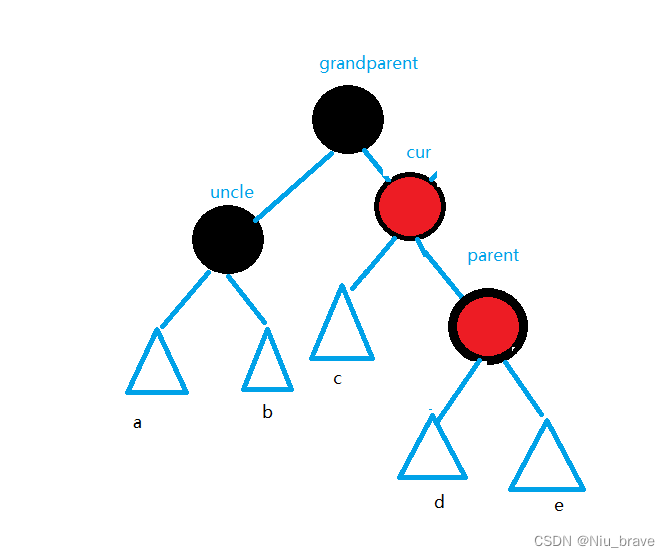
if (parent == grandparent->_right) { if (cur == parent->_right) { RevolveL(grandparent);//旋转+变色 parent->_colour = BLACK; grandparent->_colour = RED; break; } }2,右左+变色
要发生这样调整的情况:parent在grandparent的右边,cur在parent的左边。
示意图如下:
要调整这种情况,首先得以parent为中心右旋:变成左边高
然后再以grandparent为中心左旋:
然后变色:cur变黑,grandparent变红。
代码:
else if(cur == parent->_left) { RevolveR(parent);//先右旋 RevolveL(grandparent); //变色 cur->_colour = BLACK; grandparent->_colour = RED; break; }3,右+变色
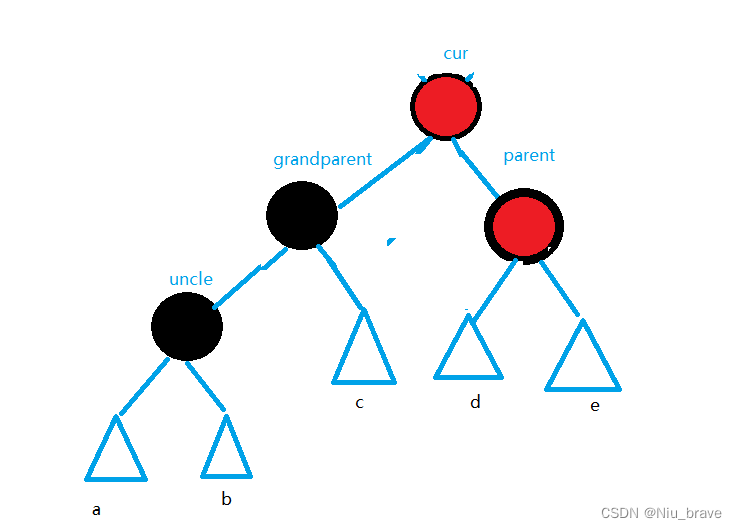
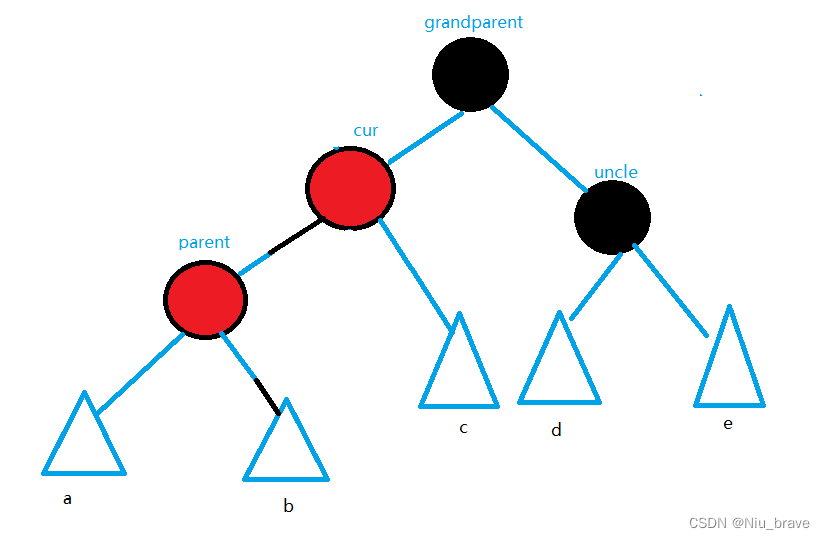
发生这种变色的情况如下:parent在grandparent的左边,cur在parent的左边。
如下图所示:
在这种情况下我要先右旋:
然后再变色:parent的颜色变黑,grandparent的颜色变红
代码:
if (cur == parent->_left) { RevolveR(grandparent); parent->_colour = BLACK; grandparent->_colour = RED; break; }4,右左+变色
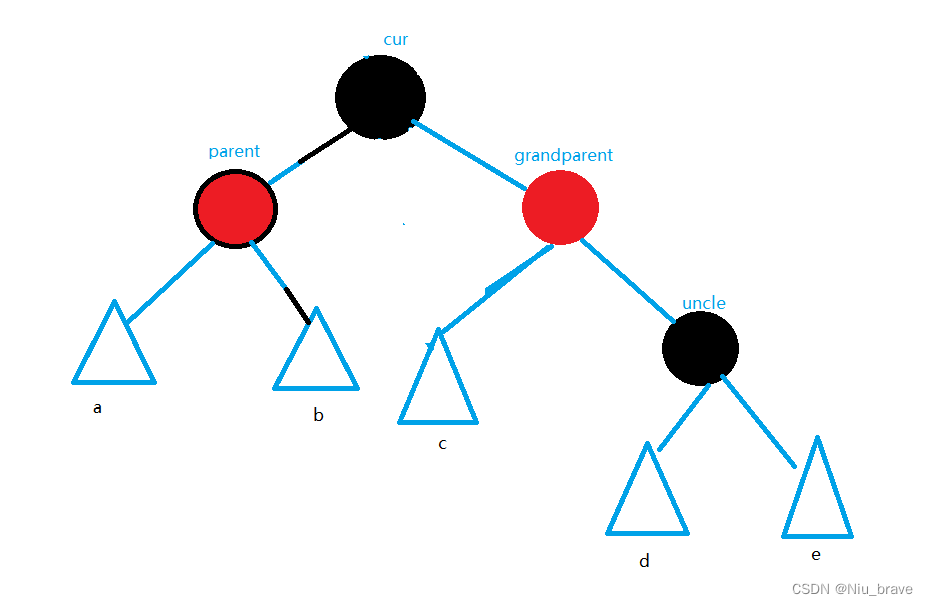
发生这种调整的情况是:parent在grandparent的左边,cur在parent的右边。如下图:
调整策略如下:
1.先以parent为中心左旋:
再以grandparent为中心向右旋转:
然后再变色:
代码如下:
else if(cur == parent->_right) { RevolveL(parent); RevolveR(grandparent); grandparent->_colour = RED; cur->_colour = BLACK; break; }
调整的整体代码如下:while (parent && parent->_colour == RED) { if (parent == _root) { break; } //找叔叔 if (parent == grandparent->_left) { uncle = grandparent->_right; } else { uncle = grandparent->_left; } if (uncle&&uncle->_colour == RED)//只变色 { grandparent->_colour = RED; uncle->_colour = BLACK; parent->_colour = BLACK; //向上调整,因为grandparent节点的颜色原来为BLACK,现在改为RED。可能会发生冲突情况,所以要向上调整。 cur = grandparent; parent = cur->_parent; } else if (uncle == nullptr || uncle->_colour == BLACK) { if (parent == grandparent->_right) { if (cur == parent->_right) { RevolveL(grandparent); parent->_colour = BLACK; grandparent->_colour = RED; break; } else if(cur == parent->_left) { RevolveR(parent);//先右旋 RevolveL(grandparent); //变色 cur->_colour = BLACK; grandparent->_colour = RED; break; } } else if (parent == grandparent->_left) { if (cur == parent->_left) { RevolveR(grandparent); parent->_colour = BLACK; grandparent->_colour = RED; break; } else if(cur == parent->_right) { RevolveL(parent); RevolveR(grandparent); cur->_colour = BLACK; grandparent->_colour = RED; break; } } }
4,平衡检查
1,有没有连续的红节点出现。
2,每条路径上的黑色节点的个数是否相同。
检查思路如下:
1.当遇到红节点时便去查看一下他的父亲节点是否为红。
2.检查黑色节点的个数便要传入一个参考值,refblacknum,然后检查每一条路径上的黑色节点个数是否等于这个值。
代码如下:
检查平衡的函数:
bool isBlance() { if (_root == nullptr) { return true; } int blackNum = 0; Node* cur = _root; while (cur) { if (cur->_colour == BLACK) { blackNum++; } cur = cur->_left; } return check(_root, 0, blackNum); }check函数如下:
bool check(Node* root, int Num, int refBlackNum) { if (root == nullptr) { if (Num != refBlackNum) { cout << "黑色节点个数不同:"; cout << _root->_kv.first << endl; return false; } return true; } if (root->_colour == RED) { if (root->_parent->_colour == RED) { cout << root->_kv.first << " " << root->_parent->_kv.first << endl; printf("出现两个连续的红节点\n"); return false; cout << root->_kv.first << endl; } } if (root->_colour == BLACK) { Num++; } return check(root->_left, Num, refBlackNum) && check(root->_right, Num, refBlackNum); }
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 一招搞定msvcr100.dll缺失问题,msvcr100.dll丢失的多种解决方法
- 全国10米分辨率植被覆盖(FVC)数据集
- android实战之Lifecycle感知组件生命周期
- SSL证书是什么?为什么需要SSL证书?
- 链接全域直播产业经济,天府锋巢直播产业基地10层正式起航
- [MySQL] 数据库的主从复制和读写分离
- 将WAP网站封装成App体验的全新策略
- 51单片机R0-R7的功能及作用
- 二分图最大匹配——匈牙利算法详解
- Unity WebView 中文输入支持