【本科生机器学习】【Python】【北京航空航天大学】课题报告：支持向量机（Support Vector Machine，SVM）初步研究【中、实验部分（一）】

说明：
（1）、仅供个人学习使用；
（2）、本科生学术水平有限，故不能保证全无科学性错误，本文仅作为该领域的学习参考。

实验原理部分见【上、原理部分】。

实验内容（及结论）

一、实验一

1、实验描述： 仅基于花瓣宽度这一个特征，训练一个逻辑斯谛分类器来检测维吉尼亚鸢尾花。

2、实验主要步骤：
（1）、数据预处理流程：

加载数据：

iris = datasets.load_iris()

建立训练集：

X = iris[“data”][:, 3:]  # 花瓣宽度字段
y = (iris[“target”] == 2).astype(int)  # 判断是否为维吉尼亚鸢尾

（2）、分类算法实现：

训练一个逻辑斯谛回归模型：

log_reg = LogisticRegression()
log_reg.fit(X, y)

将训练好的模型可视化：

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris virginica")
plt.xlabel("petal width(cm)")
plt.ylabel("probability")
plt.legend()
plt.show()

使用模型进行预测（分类）：

print(log_reg.predict([[1.7]]))  # 1
print(log_reg.predict([[1.5]]))  # 2
print(log_reg.predict([[1.9]]))  # 3
print(log_reg.predict([[0.3]]))  # 4
print(log_reg.predict([[2.6]]))  # 5

3、实验全部代码（使用Python）：

# 实验一
# 仅基于花瓣宽度这一个特征，创建一个分类器来检测维吉尼亚鸢尾花。

import numpy as np
from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression

iris = datasets.load_iris()  # 加载鸢尾花数据集
print("数据键分别为：", list(iris.keys()))

X = iris["data"][:, 3:]  # petal width
y = (iris["target"] == 2).astype(int)  # 1 if Iris virginica, else 0

# 训练一个逻辑斯谛回归模型：
log_reg = LogisticRegression()
log_reg.fit(X, y)

# 花瓣宽度在0~3cm之间的鸢尾花，模型估算出的概率：
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris virginica")
plt.xlabel("petal width(cm)")
plt.ylabel("probability")
plt.legend()
plt.show()

# 使用模型作出预测：
print(log_reg.predict([[1.7]]))  # 1
print(log_reg.predict([[1.5]]))  # 2
print(log_reg.predict([[1.9]]))  # 3
print(log_reg.predict([[0.3]]))  # 4
print(log_reg.predict([[2.6]]))  # 5

4、实验结论

（1）、估计的概率和决策边界（Decision Boundary, DB）图示：

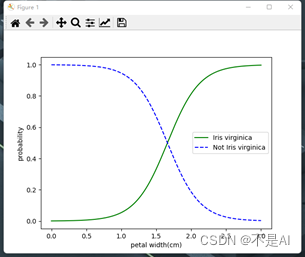
图6.逻辑斯谛回归分类器的决策边界

输出结果解释：图6中，绿色实线代表维吉尼亚鸢尾花出现的概率与花瓣宽度之间的关系，蓝色虚线代表其他两种鸢尾花（非维吉尼亚）出现的概率与花瓣宽度之间的关系。通过两条线的交点并垂直于横轴的直线为分类器的决策边界。在决策边界左侧的数据，分类器输出“0”，在决策边界右侧的数据，分类器输出“1”。

（2）、模型对数据的预测

选取的5个测试数据点的预测结果：

[1], [0], [1], [0], [1]

结果解释：
输出“1”代表维吉尼亚鸢尾，输出“0”代表其他鸢尾。
花瓣宽度为1.7cm的鸢尾花，模型将其归入维吉尼亚鸢尾。花瓣宽度为1.5cm的鸢尾花，模型将其归入非维吉尼亚鸢尾。其余类似。
predict()方法返回一个可能性最大的类别。即在大约1.6cm处存在一个决策边界，在边界处“是”或“不是”的概率均为50%。如果花瓣宽度大于1.6cm，分类器就预测它是维吉尼亚鸢尾花，否则就预测不是，即便这样的输出不一定正确。

二、实验二

1、实验描述： 训练线性SVM模型，根据花瓣的长度和花瓣宽度来检测维吉尼亚鸢尾花。

2、实验主要步骤：

（1）、数据预处理流程：

加载数据：

iris = datasets.load_iris()

建立训练集：

X = iris[“data”][:, 3:]  # 花瓣宽度字段
y = (iris[“target”] == 2).astype(int)  # 判断是否为维吉尼亚鸢尾

缩放特征，使决策边界看起来更明显：

svm_clf = Pipeline([  # 线性SVM模型
    ("scaler", StandardScaler()),  # 特征缩放
    ("linear_svc", LinearSVC(C=1, loss="hinge", max_iter=5000)),
    ])

（2）、实验算法实现：

使用C = 1的LinearSVC类和hinge损失函数建立线性SVM模型，为避免Liblinear无法收敛，将最大迭代次数设置为5000：

svm_clf = Pipeline([  # 线性SVM模型
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge", max_iter=5000)),
    ])

训练SVM模型：

svm_clf.fit(X, y)

使用训练好的模型进行预测：

# 使用模型进行预测:
print(svm_clf.predict([[5.5, 1.7]]))   # 1
print(svm_clf.predict([[4.0, 2.0]]))   # 2
print(svm_clf.predict([[4.25, 1.5]]))  # 3
print(svm_clf.predict([[5.6, 1.45]]))  # 4
print(svm_clf.predict([[5.75, 2.5]]))  # 5

3、实验全部代码（使用Python）：

# 实验二
# 基于花瓣长度和花瓣宽度两个特征，训练线性SVM模型来检测维吉尼亚鸢尾花

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()  # 加载鸢尾花数据集

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris virginica

svm_clf = Pipeline([  # 线性SVM模型
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge", max_iter=5000)),
    ])

svm_clf.fit(X, y)

# 使用模型进行预测:
print(svm_clf.predict([[5.5, 1.7]]))   # 1
print(svm_clf.predict([[4.0, 2.0]]))   # 2
print(svm_clf.predict([[4.25, 1.5]]))  # 3
print(svm_clf.predict([[5.6, 1.45]]))  # 4
print(svm_clf.predict([[5.75, 2.5]]))  # 5

4、实验结论

（1）、 生成的模型：

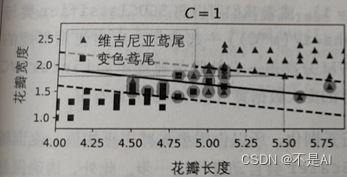
图7.SVM模型

解释：图7中的实线代表SVM分类器的决策边界，这条线不仅分离了两个类，并且尽可能地远离了最近的训练实例，提高了模型的泛化性。

（2）、使用模型进行预测：

选取的5个测试数据点的预测结果：

[1], [1], [0], [0], [1]

结果解释：在C = 1的情况下，SVM将花瓣长度为5.5cm,花瓣宽度为1.7cm的样本归于维吉尼亚鸢尾。其余样本类似。

三、实验三

1、实验描述： （承接实验二）改变实验二中SVM模型超参数C的值，观察分类器的输出变化。

2、实验主要步骤：

（1）、数据预处理流程：

同实验二。

（2）、算法思想及步骤：

将SVM分类器的超参数C设定为1，并在训练集上训练模型：

# 第一个svm分类器，指定超参数C = 1
svm_clf1 = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge", max_iter=5000)),
])

svm_clf1.fit(X, y)

将SVM分类器的超参数C设定为100，在训练集上训练模型：

# 第二个svm分类器，指定超参数C = 100
svm_clf2 = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=100, loss="hinge", max_iter=5000)),
])

svm_clf2.fit(X, y)

在测试集上，用模型进行分类测试：

# 使用第一个模型进行分类测试
print(svm_clf1.predict([[5.5, 1.7]]))   # 1
print(svm_clf1.predict([[4.0, 2.0]]))   # 2
print(svm_clf1.predict([[4.25, 1.5]]))  # 3
print(svm_clf1.predict([[5.6, 1.45]]))  # 4
print(svm_clf1.predict([[5.75, 2.5]]))  # 5

print()

# 使用第二个模型进行分类测试
print(svm_clf2.predict([[5.5, 1.7]]))   # 1
print(svm_clf2.predict([[4.0, 2.0]]))   # 2
print(svm_clf2.predict([[4.25, 1.5]]))  # 3
print(svm_clf2.predict([[5.6, 1.45]]))  # 4
print(svm_clf2.predict([[5.75, 2.5]]))  # 5

3、实验全部代码（使用Python）：

# 实验三
# 改变SVM模型超参数C的值，观察分类器的输出变化。

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()  # 加载鸢尾花数据集

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris virginica

# 第一个svm分类器，指定超参数C = 1
svm_clf1 = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge", max_iter=5000)),
])

svm_clf1.fit(X, y)

# 第二个svm分类器，指定超参数C = 100
svm_clf2 = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=100, loss="hinge", max_iter=5000)),
])

svm_clf2.fit(X, y)

# 使用第一个模型进行分类测试
print(svm_clf1.predict([[5.5, 1.7]]))   # 1
print(svm_clf1.predict([[4.0, 2.0]]))   # 2
print(svm_clf1.predict([[4.25, 1.5]]))  # 3
print(svm_clf1.predict([[5.6, 1.45]]))  # 4
print(svm_clf1.predict([[5.75, 2.5]]))  # 5

print()

# 使用第二个模型进行分类测试
print(svm_clf2.predict([[5.5, 1.7]]))   # 1
print(svm_clf2.predict([[4.0, 2.0]]))   # 2
print(svm_clf2.predict([[4.25, 1.5]]))  # 3
print(svm_clf2.predict([[5.6, 1.45]]))  # 4
print(svm_clf2.predict([[5.75, 2.5]]))  # 5

4、实验结论

（1）、 C = 1与C = 100时模型的对比：

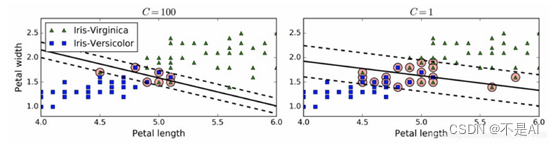
图8.更少的间隔冲突（左）和大间隔（右）

对结果的解释：超参数C的作用是在保持“街道”（虚线之间的区域）宽阔和限制间隔违例（即位于街道之上，甚至在错误的一边的实例）之间找到良好的平衡。这就是软间隔分类。
左图为C值较高(C=100)时分类器模型，分类器的错误样本（间隔违例）较少，但是间隔也较小，导致模型对异常值比较敏感，泛化能力弱；
右图为C值较低(C=1)时分类器模型，分类器的间隔大了很多，但是位于间隔之间的实例也更多。该模型的泛化性更好，因为大多数间隔违例实际上都位于决策边界（实线）正确的一边。

（2）、 对模型的测试：

第1个模型的预测结果：

[1], [1], [0], [0], [1]

第2个模型的预测结果：

[1], [0], [0], [1], [1]

其中“1”代表维吉尼亚鸢尾，“0”代表变色鸢尾。
对结果的解释：可以看出，2个模型的输出大致相同，但是在边界数据点（序号为2、4）上，输出的分类结果并不相同，可见C = 1时的模型泛化性更好。

实验部分（一） 到此结束。