【UnityShader入门精要学习笔记】第四章(1)坐标系

本系列为作者学习UnityShader入门精要而作的笔记,内容将包括:
- 书本中句子照抄 + 个人批注
- 项目源码
- 一堆新手会犯的错误
- 潜在的太监断更,有始无终
总之适用于同样开始学习Shader的同学们进行有取舍的参考。
(该系列笔记中大多数都会复习前文的知识,特别是前文知识非常重要的时候,这是为了巩固记忆,诸位可以直接通过目录跳转)
(第四章内容请参考修改稿)
前言
计算机图形学是建立在虚拟世界上的数学模型,因此数学也渗透到了图形学的方方面面。在学习Shader的过程中,我们最常用的就是矢量和矩阵(计算机的重要基础之一——线性代数)。
(这里建议大家提前预习,观看3blue1brown的线性代数的本质一课,会有很大收获,强烈建议大家在学习第四章前先去看看该系列视频,一定对你理解线性代数有很大帮助,坐标系较为简单,因此本章大部分内容被浓缩了 )
学习数学可以便于我们在学习研究他人编写的Shader时理解其中的原理所在。
在笔者看来,想要深耕计算机领域,必不可少的有三大能力:英文读写能力,数学计算能力,逻辑思维能力。诸位不应当看到这些而感到畏惧,像笔者本人的这三种属性都属于中下游。但是我相信只要将这三种能力贯穿于生活中的方方面面,即使天资愚钝,长久努力下也可以得到提升。
在该书中作者给出了一些练习题,我会穿插到笔记之中,如果可以希望读者们与我一同练习。
假定我们在开发一款农场游戏,主角是农场的一头牛——妞妞,让我们看看数学会为农场带来什么变化?
笛卡尔坐标系
什么是笛卡尔坐标系
笛卡尔坐标系(Cartesian Coordinate System) 是数学上重要的基础概念之一,从小学的直角坐标系开始,我们就已经接触到笛卡尔坐标系。
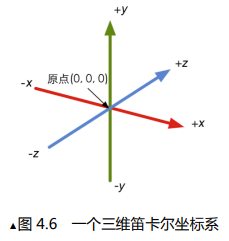
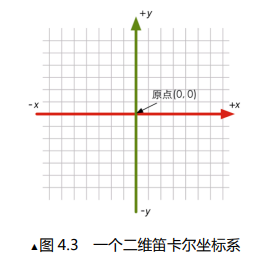
当然,诸位经过九年义务教育之后肯定对坐标系熟悉的不能再熟悉了。笛卡尔坐标系中包含了以下要素:
- 原点,它是整个坐标系的中心,我们以0坐标代表该点
- n维笛卡尔坐标系中的n个轴都是两两正交的,例如上图三维笛卡尔坐标系,xy,xz,yz都互相垂直。(为什么是n个轴,我们三维生物还能描述四维坐标轴吗?当然可以,你不能描述不代表数学不能)
(正交是什么意思?你可以理解为几何上它们相互垂直;如果两个向量是相互正交的,那么在代数上它们的向量内积为0;如果一个矩阵是正交的,那么该矩阵乘上它的转置矩阵的结果为单位矩阵E)
(在三维软件中,我们喜欢以红色直线代表x轴,绿色直线代表y轴,蓝色直线代表z轴)
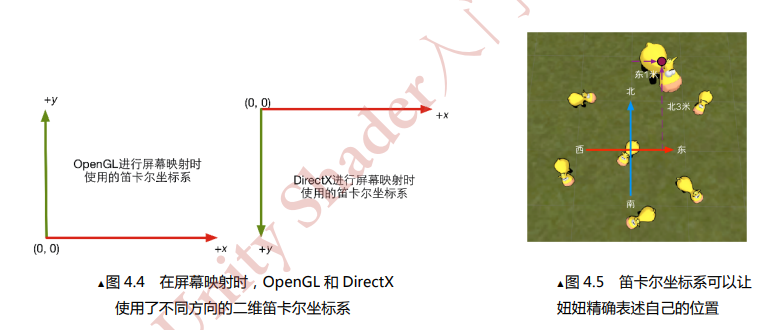
三维坐标系
再多嘴介绍一下笛卡尔坐标系中的一些基本概念,过原点的直线被我们称为基矢量,或者大家更喜欢叫它轴 。我们以每条轴箭头指向的方向为正方向,反向为负方向。以正方形上的单位长度称为基向量( 或者基底 ,或者标准正交基)。当然,在非正交坐标系下,例如我们之前提到过的中心坐标系,其基向量就不是正交的。
左右手坐标系
在三维空间中,有两种不同类型的坐标系:左手坐标系 和 右手坐标系 。
为什么三维中有两种不同的坐标系,而二维没有呢?这是因为二维中即使坐标轴的指向方向不同,我们也可也通过在三维空间上的翻转使得不同的坐标轴指向方向相同。
而在三维空间中,这种旋转有时就无法使得两个坐标系重合了。我们可以使得其中两个轴的方向相同,但第三条轴的方向始终是相反的。
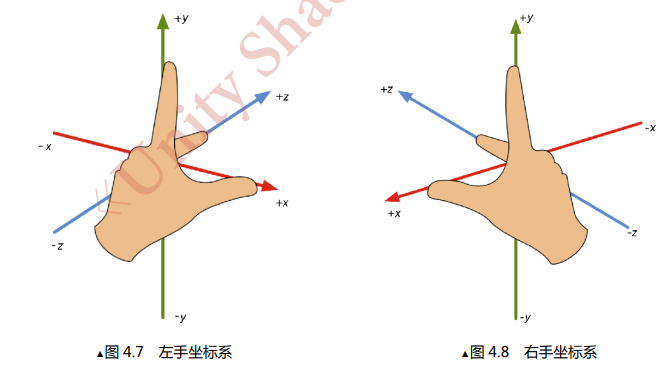
请各位举起左手,用食指和大拇指摆出L的手势,并使食指指向上(y轴正方向),大拇指指向右(x轴正方向),中指自然伸出(它指向z轴正方向)。现在你的左手就构成了一个左手坐标系。同样的,伸出右手,如图所示,构建一个右手坐标系。
只有相同的坐标系才能够通过旋转的方式使得两个坐标系重合,我们将这种性质称为旋向性(handedness) 。
判断坐标系的简单方法就是伸出任意一只手,并将手指向当前坐标对应的轴的正方形,使得两条轴与食指大拇指指向方向重合,如果剩余的一条轴的正方向不是中指的指向方向,就代表当前坐标系不是左手/右手坐标系,反之代表是。
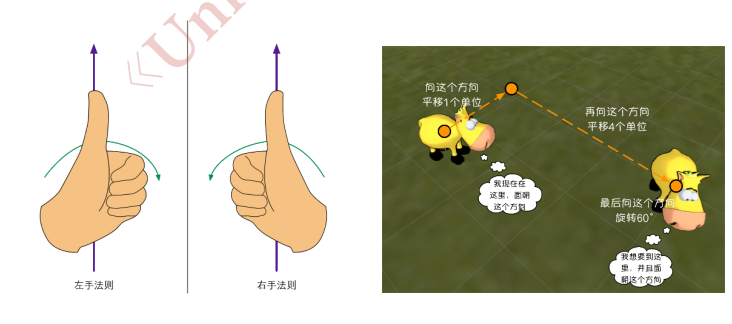
同样的,对于旋转的定义,两个坐标系也不同,还记得初高中物理判断线圈中电流方向的左右手法则 吗?虚握左手/右手,大拇指指向轴,四指弯曲方向即为旋转正方向。在左手坐标系中,旋转方向由左手法则定义,右手坐标系中则为右手法则定义。
在左手坐标系中,旋转正方向为顺时针,而在右手坐标系中,旋转正方向为逆时针。
当然,左右手坐标系也可以相互转换,只需反转其中任意一条轴的方向即可。
我们之所以要引入坐标系,其根本目的就是为了在空间中描述某个点的位置。而在Unity等等三维软件中,我们固定了一个唯一的初始坐标,才能够统一的描述这个三维软件的空间内的所有物体。
在上图右侧,妞妞想要从起始点到达终点,需要往某个方向移动一个单位,再向另一个方向移动4个单位,最后再向这个方向旋转60度。以上描述含糊不清,引入了坐标系之后,我们就能很轻易的描述妞妞的运动了。
Unity使用的坐标系
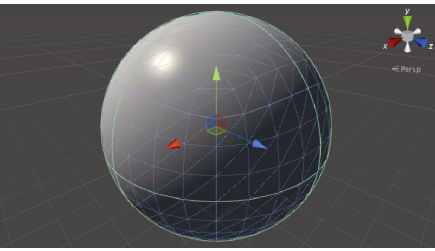
Unity中,对于模型空间和世界空间,Unity使用的是左手坐标系。这可以从Scene视图的坐标轴显示看出来。
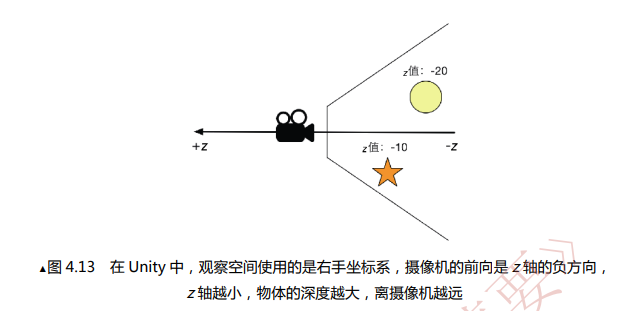
而对于观察空间来说,Unity使用的是右手坐标系。简单来说就是以摄像机为原点的坐标系,再这个坐标系中,摄像机的镜头方向是z轴的负方向(也就是z轴的正方向实际上是从屏幕指向屏幕前的你),这与模型空间和世界空间中的定义相反,z轴的减少意味着场景深度的增加。
练习题
练习题答案将在下一章复习时给出。
- 3dMax中,默认坐标轴方向为:x轴正方向指向右方,y轴正方形指向前方,z轴正方形指向上方,那么它是左手还是右手坐标系?
- 左手坐标系中,有一个点是(0,0,1),如果将该点绕y轴正方向旋转+90°,旋转后的坐标为?如果在右手坐标系同样有一个点是(0,0,1),把它绕y轴正方形旋转+90°,旋转后的坐标为?
- 在Unity中,新建场景的主摄像机位于世界空间的(0,1,-10)位置。在不改变摄像机的任何设置的情况下,在世界空间的(0,1,0)位置新建一个球体,如图所示:

在该摄像机的观察空间下,该球体的z值是多少?在摄像机的模型空间下(以该摄像机在上图中的位置为原点建立坐标系),该球体的z值又是多少?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 电动夹爪可用TMC方案推荐
- 热门免费API接口,含天气api、物流API、企业工商API等
- Linux免密实现文件拷贝(建立机器之间的SSH密钥认证)
- SpringBoot代码混淆与反混淆加密工具详解
- C#,冒泡排序算法(Bubble Sort)的源代码与数据可视化
- 开机0xc000000e修复方式,电脑出现错误代码0xc000000e
- Matlab定义函数计算斐波那契数列
- Vue前端规范【二】
- java热点话题
- JRT控制打印机