acwing-蓝桥杯C++ AB组辅导课Day2-递归习题+递推+二分

发布时间：2023年12月20日

感谢梦翔老哥的蓝桥杯C++ AB组辅导课~

递归习题：


1.递归实现组合型枚举

题意：

题目要求输出组合枚举，与排列不同，排列具有顺序之分，对于组合来说，是没有顺序之分的，所以[1,2,3]和[3,2,1]被看成同一种组合。

所以想要输出正确答案，最好的办法就是人为的为结果添加顺序。无论是递增或递减都可以。

代码如下：

之前的办法，这个思路更巧妙，巧妙的地方体现在不需要更多的顺序判别。顺序的定义在for(int i = start;i<=n;i++)体现。每次循环只能从比较小的数向更大的数枚举，从而保证了顺序。并且加入了剪枝，当已经填好位置的数的数量与尚未添加的数的总和少于位置数，说明肯定填不满，就可以返回了。

#include<bits/stdc++.h>

using namespace std;

int ans[30];

int m,n;    //m表示位置个数，n表示数字个数

void dfs(int u,int start){//枚举位置
    if(u+n-start+1<m) return;
    if(u == m){
        for(int i=0;i<m;i++){
            cout<<ans[i]<<" ";
        }
        cout<<endl;
        return;
    }
    for(int i=start;i<=n;i++){
            ans[u] = i;;
            dfs(u+1,i+1);
            ans[u] = 0;
    }
    
    
}

int main(){
    cin>>n>>m;
    
    dfs(0,1);
    
    return 0;
}

2.带分数

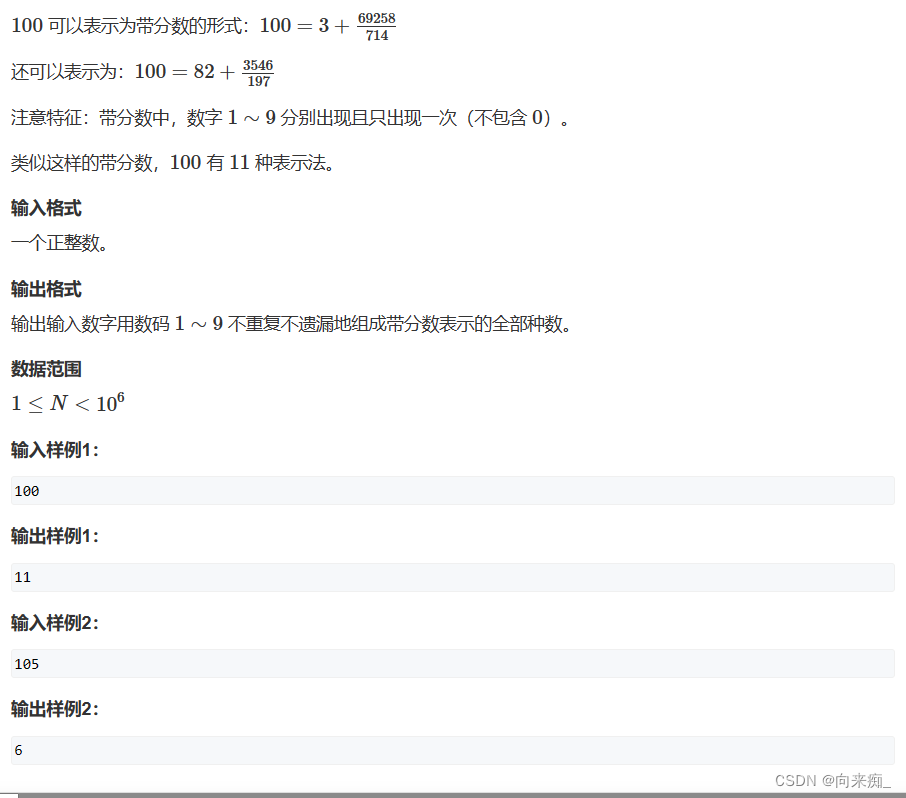
解题思路：

? ? ? ? （1）暴力枚举所有排列，用两个隔板划分出a,b,c。再判断。复杂度为9！*9*?$\binom{2}{8}$。差不多是9*10^{_{7}}，刚好满足时间复杂度。

? ? ? ? （2）上一个思路相当于暴力枚举了三个数a,b,c。并且没有用上题目给的n，样例中n=100。根据题目中包含的等式a+b/c = n -> a*c + b = n*c。只需要枚举a和c两个数，根据n可以将b算出来。这样枚举的数字减少，可以有效减少时间复杂度。

先枚举a,在a的叶子节点枚举c，再判断等式是否成立，若成立则增加计数。

代码：

有几个需要注意的点，这种方式代码很容易出错。dfs_a函数中递归边界为a>=n。dfs_c的递归边界为位置是否占满。check函数中主要判断1-9的数字是否全部使用，此时不应该使用原来的st数组，应该新建backup数组，因为st数组用来保持回溯，check函数中对bool数组的操作无法保证恢复现场。

?
#include<bits/stdc++.h>

using namespace std;

const int N = 20;

int n;
bool st[N], backup[N];

int cnt = 0;

bool check(int a,int c){
    int b = n*c - a*c;
    memcpy(backup,st,sizeof st);
    if(!a || !b || !c) return false;
    while(b){
        int i = b%10;
        b/=10;
        if(!i||backup[i]) return false;
        backup[i] = true;
    }
    for(int i=1;i<=9;i++){
        if(!backup[i]) return false;
    }
    return true;
}


void dfs_c(int u,int a, int c){
    if(u == 9) return;
    if(check(a,c)) cnt++;
    for(int i=1;i<=9;i++){
        if(!st[i]){
            st[i] = true;
            dfs_c(u+1,a,c*10+i);
            st[i]= false;
        }
    }
}

void dfs_a(int u,int a){    //u表示已经填了几个位置
    if(a>=n) return;
    if(a) dfs_c(u,a,0);
    for(int i=1;i<=9;i++){
        if(!st[i]){
            st[i] = true;
            dfs_a(u+1,a*10+i);
            st[i] = false;
        }
    }
    
}

int main(){
    cin>>n;
    
    dfs_a(0,0);
    
    cout<<cnt<<endl;
    return 0;
    
}

?

递推与递归的区别：
递归是从目标开始自顶向下的找同类子问题的解，最后解决原问题。而递推是自底向上先求子问题，根据子问题的解解决原问题。

递推例题：

1.简单斐波那契

代码：

#include<bits/stdc++.h>

using namespace std;

int main(){
    int n;
    cin>>n;
    int f[46]={0};
    f[1] = 0;
    f[2] = 1;
    for(int i = 3;i<=n;i++){
        f[i] = f[i-1] + f[i-2];
    }
    for(int i=1;i<=n;i++){
        cout<<f[i]<<" ";
    }
    return 0;
}

采取滚动数组的思想：

#include<bits/stdc++.h>

using namespace std;

int main(){
    int n;
    cin>>n;
    int a = 0,b = 1;
    for(int i = 1;i<=n;i++){
        cout<<a<<" ";
        int f = a+b;
        a = b;
        b = f;
    }

    return 0;
}

2.费解的开关

题目链接：95. 费解的开关 - AcWing题库

题意：

改变一个灯的状态会将他上下左右的灯的状态都改变。需要使用最少次数修改灯的状态使得所有的灯变成亮着的。

解题思路：

找到题目隐藏信息，1.所有开关只能按一次，按两次相当于没按。2.灯的状态跟按开关的顺序无关，无论以什么顺序按开关，灯的状态相同。

我们发现，假如可以枚举第一行的操作（是否按开关），枚举完后，我们不能对第一行再进行操作（因为所有开关只能按一次，并且我们枚举了第一行的按开关的所有操作），此时我们需要按第二行的开关，并且操作被第一行灯的亮灭状态所唯一决定。（递推）当第二行操作结束后，第三行的操作也被唯一决定。以此类推，直到n-1行操作完成，此时前n-1行的状态全部为亮，只需查看最后一行是否为量即可判断该方案是否可取，如果可取，更新最小答案。

代码：
代码实现有不少细节的地方，比如turn函数中传入坐标x,y不能直接使用，应该用a,b代替。因为坐标会在for循环中被修改，而实际上传进来的x,y坐标不应该变。

还有就是memcpy函数对原数组进行备份， 因为for循环枚举所有方案，每次方案开始时要保证都是原来的数组，所以要备份。在每个方案结束后再将数组还原。

#include<bits/stdc++.h>
using namespace std;
char light[6][6],backup[6][6];

int dx[5]={0,1,0,-1,0},dy[5]={1,0,-1,0,0};
void turn(int x,int y){
    
    for(int i=0;i<5;i++){
        int a = x + dx[i];
        int b = y + dy[i];
        if(a<0||a>=5||b<0||b>=5) continue;
        if(light[a][b] == '0') light[a][b] = '1';
        else light[a][b] = '0';
    }
    return;
}

int main(){
    int n;
    cin>>n;
    for(int a=0;a<n;a++){
        for(int i=0;i<5;i++) cin>>light[i];
        int res = 10;
        for(int op=0;op<32;op++){
            memcpy(backup,light,sizeof light);
            int step = 0;
            for(int k=0;k<5;k++){
                if(op>>k&1){
                    turn(0,k);
                    step++;
                    // cout<<1111<<endl;
                }
            }
            for(int i=0;i<4;i++){
                for(int j=0;j<5;j++){
                    if(light[i][j] == '0'){
                        turn(i+1,j);
                        step++;
                    }
                }
            }
            bool dark = false;
            for(int i=0;i<5;i++){
                if(light[4][i] == '0') dark = true;
            }
            if(!dark) res = min(res,step);
            memcpy(light,backup,sizeof backup);
        }
        if(res>6) res = -1;
        cout<<res<<endl;
    }
    return 0;
}

递归习题：

1.翻硬币

解题思路：

挖掘题目信息1.所有硬币的中间相当于有个开关，按一次会将开关两侧的硬币翻转。2.按开关的顺序与硬币状态无关。3.开关只能按一次，按两次相当于没按。

考虑按顺序按开关，发现假如前面的开关已经按下的话，后面开关是否需要被按被前面硬币的状态所唯一决定。（递推）所以按顺序按开关就完事了。

代码：

#include<bits/stdc++.h>

using namespace std;

string a,b;
void turn(int i){
    if(a[i]=='*'){
        a[i] = 'o';
        if(a[i+1] == '*'){
            a[i+1] = 'o';
        }else{
            a[i+1] = '*';
        }
    }else{
        a[i] = '*';
        if(a[i+1] == '*'){
            a[i+1] = 'o';
        }else{
            a[i+1] = '*';
        }
    }
    return;
}


int main(){
    cin>>a;
    cin>>b;
    int n = a.size();
    int step = 0;
    for(int i=0;i<n-1;i++){
        if(a[i]!=b[i]){
            turn(i);
            step++;
        }
    }
    cout<<step;
    return 0;
}

2.飞行员兄弟

题目链接：116. 飞行员兄弟 - AcWing题库

题意：
费解的开关的简化版，需要令一个4x4的矩阵全部变成'-'。矩阵的字符可能为'+'或'-'。当按动一个开关，同列的状态和同行的状态都会被改变。题目要求输出最小步骤数和操作的开关位置。

解题思路：
由于题目范围不大，只有总共16个数，可以考虑指数型枚举所有开关的操作。复杂度为2^16。对于每个操作，判断结果是否符合预期，如果符合，那么更新最小步骤数。

代码：

代码实现方面有个小点没想到，在turn函数中for循环中会令[x,y]处状态修改两次，所以后面要单独再修改一次。

#include<bits/stdc++.h>

using namespace std;
char fridge[5][5],backup[5][5];

void turn(int x,int y){
    for(int i=0;i<4;i++){
        if(fridge[x][i] == '+'){
            fridge[x][i] = '-';
        }else fridge[x][i] = '+';
        
        if(fridge[i][y] == '+'){
            fridge[i][y] = '-';
        }else fridge[i][y] = '+';
    }
    //经过前面的处理，[x,y]的位置会被修改两次，这里要修改回来。
    if(fridge[x][y] == '+'){
            fridge[x][y] = '-';
        }else fridge[x][y] = '+';
    return;
}


int main(){
    for(int i=0;i<4;i++) cin>>fridge[i];
    int res = 100;
    vector<pair<int,int>> ans;
    for(int op=0;op<65536;op++){
        memcpy(backup,fridge,sizeof fridge);
        int step = 0;
        vector<pair<int,int>> sp;
        for(int i=0;i<16;i++){  //枚举每一位
            if(op>>i&1){
                int x = i/4;
                int y = i%4;
                turn(x,y);
                // cout<<x<<y<<endl;
                sp.push_back({x,y});
                step++;
            }
        }
        //判断方案是否可行
        bool yes = true;
        for(int i=0;i<4;i++){
            for(int j=0;j<4;j++){
                if(fridge[i][j] == '+'){
                    yes = false;
                    // break;
                }
            }
            // if(!yes) break;
        }
        if(yes&&step<res){
            cout<<step<<endl;
            res = step;
            ans = sp;
        }
        memcpy(fridge,backup,sizeof backup);
    }
    // cout<<ans.size()<<endl;
    for(int i=0;i<ans.size();i++){
        cout<<ans[i].first+1<<' '<<ans[i].second+1<<endl;
    }
    return 0;
}

整数二分问题的思路：

模板使用的时候只需要判断是L=M还是R=M，据此判断使用模板1还是模板2。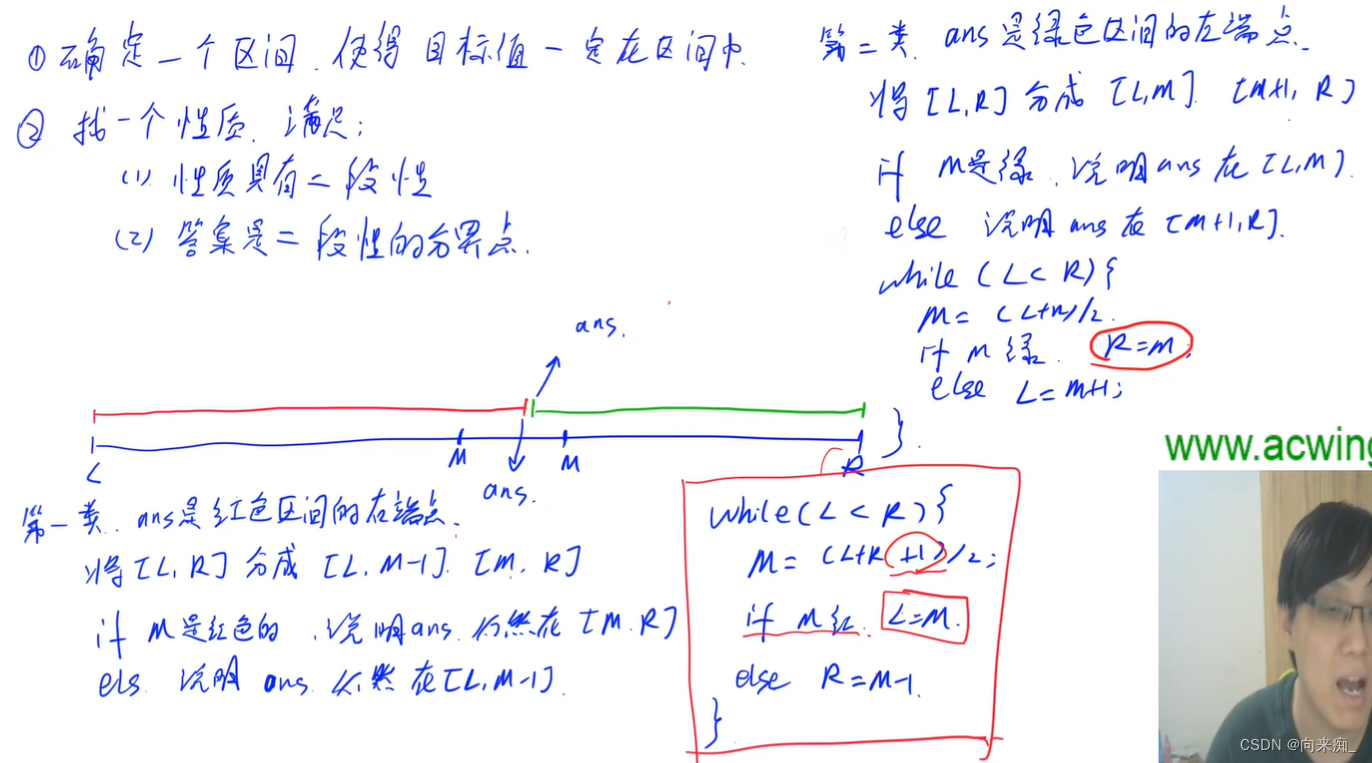

二分例题：

1.数的范围

题目链接：789. 数的范围 - AcWing题库

题意：给n个非递减的数，找出某个数值的起始位置和结束位置。

二分模板的选择：

选右区间的左端点时选第一个模板，选左区间的右端点时选第二个模板。

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

解题思路：
首先考虑题目是否可以二分，答案一定在题目给定的区间范围内，并且可以使用二段性（是否大于等于/小于等于）分隔区间，并且答案是区间的端点，所以可以使用二分。

代码：
二分起始位置时，因为判断的是是否大于等于目标值，所以答案是右区间的左端点，所以使用模板1，二分结束位置时，因为判断的是是否小于等于目标值，所以答案是左区间的右端点，所以使用模板2。

#include<bits/stdc++.h>

using namespace std;
int num[100010];
int main(){
    int n,q;
    cin>>n>>q;
    for(int i=0;i<n;i++) scanf("%d",&num[i]);
    while(q--){
        int k ;
        cin>>k;
        int l = 0,r = n-1;
        while(l<r){
            int mid = l+r>>1;
            if(num[mid]>=k) r = mid;
            else l = mid+1;
        }
        if(num[l] == k){
            cout<<l<<' ';
            l = 0;
            r = n-1;
            while(l<r){
                int mid = l+r+1>>1;
                if(num[mid]<=k) l = mid;
                else r = mid-1;
            }
            cout<<l<<endl;
        }else{
            cout<<"-1 -1"<<endl;
        }
    }
    return 0;
}

2.数的三次方根

题目链接：790. 数的三次方根 - AcWing题库

题意：给一个数，找它的三次方根。

解题思路：

直接二分区间，判断mid的三次方是否小于真值，更新区间即可。

代码：

#include<bits/stdc++.h>

using namespace std;

int main(){
    double n;
    cin>>n;
    double l = -10000,r = 10000;
    while(r-l>1e-8){
        double m = (l+r)/2;
        if(m*m*m>n){
            r = m;            
        }else l = m;
    }
    printf("%lf",l);
    return 0;
}

二分习题：

1.机器人跳跃问题

题目链接：730. 机器人跳跃问题 - AcWing题库

题意：机器人根据开始的能量值e进行跳跃，跳到比当前更高的楼会减少h[i]-e能量值，跳到比当前更低的楼会增加e-h[i]能量值，期间能量值若为负数，则失败。题目要求返回能够跳到最后一栋楼最小的能量值。

解题思路：
首先题目问能够满足条件的最小数，十分满足二分的解题思路。答案一定在题目给定的区间内，可以找到二段性，区间左侧不满足题意，区间右侧满足题意，并且我们要找的答案就是右侧区间的左端点（即最小值）。

代码：
题目细节处在于，当e＞100000时就可以确定一定能跳过所有楼层了。但如果不加判断，e有可能会不断增加，最后爆int导致错误。

#include<bits/stdc++.h>
using namespace std;

int h[100010];
int n;

bool check(int e){

    for(int i=1;i<=n;i++){
        if(h[i] > e){
            // cout<<"e:"<<e<<" h:"<<h[i]<<endl;
            e -= (h[i]-e);
        }else{
            e += (e-h[i]);      //由于差值越大，加的数越大，所以这里可能会爆int变成负数
        }
        if(e<0) return false;
        if(e>100000) return true;
    }
    return true;
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        scanf("%d",&h[i]);
    } 
    // for(int i=1;i<=n;i++) cout<<h[i]<<" ";
    //二分答案
    int  l = 1,r = 100000;
    while(l<r){
        int mid = l+r>>1;
        if(check(mid)) r = mid;
        else l = mid+1;
        // cout<<l<<' '<<r<<endl;
    }
    cout<<l<<endl;
    return 0;
}

2.四平方和

题目链接：1221. 四平方和 - AcWing题库

题意：所有数字都可以写成四个数的平方和，给一个数n,要求返回平方和等于n的字典序最小的四个数。

解题思路：
一开始想的是使用二分＋哈希，先初始化出来小于根号n的数的平方到数组。每次二分找到小于n的数的平方（左区间的右端点），并让n减去这个数的平方，循环4次，最后判断平方和是否等于n。如果不相等，更新二分区间。这种解法虽然可以找到四个数的平方和=n，但是不是字典序最小，所以不可行。

由于题目要求字典序最小，所以可以考虑从小枚举，每个位置可以枚举的数是根号下5e6，大概是2236。所以不能枚举四个位置（时间复杂度太高），最多只能枚举两个位置。所以可以考虑先枚举两个位置(c,d)的结果并存储，然后再从小枚举另外两个(a,b)的位置，这样保证a<b,c<d，再枚举a,b时用t=n-c*c-d*d暂存结果，二分之前存储的c,d查看是否有合适的结果。

代码：

细节的地方在于2500010，2500010怎么来的呢？我们可以查看sum是如何增加的，可以看到，sum[m++]的位置在c,d的循环里面，c循环的次数为根号n,d的循环次数小于根号n,sum增加的次数大概为根号n,根号n-1,根号n-2...3,2,1，求和后大概为n/2。

#include<bits/stdc++.h>

using namespace std;

struct Sum{
    int c;
    int d;
    int sum;
    bool operator< (const Sum &t)const{
        if(sum!=t.sum) return sum<t.sum;
        if(c!=t.c) return c<t.c;
        return d<t.d;
    }
}sum[2500010];
int n;
int m=0;
int main(){
    cin>>n;
    for(int c=0;c*c<=n;c++){
        for(int d=c;c*c+d*d<=n;d++){
            sum[m++] = {c,d,c*c+d*d};
        }
    }
    sort(sum,sum+m);
    
    for(int a = 0;a*a<=n;a++){
        for(int b=a;a*a+b*b<=n;b++){
            int t = n-a*a-b*b;
            int l=0,r = m-1;
            while(l<r){
                int mid = l+r>>1;
                if(sum[mid].sum>=t) r = mid;
                else l = mid+1;
            }
            if(sum[l].sum == t){
                cout<<a<<" "<<b<<" "<<sum[l].c<<" "<<sum[l].d<<endl;
                return 0;
            }
        }
    }
    return 0;
}

3.分巧克力

题目连接：1227. 分巧克力 - AcWing题库

题意：给n块h[i]*w[i]边长的巧克力，要分给k个小朋友，如何切巧克力让巧克力边长最大，并能分给所有的小朋友。

解题思路：

题目要求找巧克力边长最大，假如边长增大，那么可以切出来的巧克力块数会变少。所以想要满足分给所有的小朋友，边长较小的区间都是可以的，为左区间，左区间的右端点就是答案。

代码：
细节之处在于，h[i]*w[i]边长的巧克力对于切mid边长的巧克力，能切多少块呢？答案是h[i]/mid下取整*w[i]/mid下取整。

#include<bits/stdc++.h>

using namespace std;


int n,k;
int h[100010],w[100010];

bool check(int mid){
    
    int res = 0;
    for(int i=0;i<n;i++){
        res += (h[i]/mid) * (w[i]/mid);
        if(res >= k) return true;   
    }
    
    return false;
}

int main(){
    
    cin>>n>>k;
    for(int i=0;i<n;i++)    cin>>h[i]>>w[i];
    
    int l = 1, r = 100000;
    while(l<r){
        int mid = l+r+1>>1;
        if(check(mid)) l = mid;
        else r = mid-1;
    }
    
    cout<<l<<endl;
    return 0;
}

文章来源:https://blog.csdn.net/weixin_52861033/article/details/135029914
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章