excel统计分析——S-W正态性检验

发布时间：2023年12月24日

参考资料：

[1]马兴华,张晋昕.数值变量正态性检验常用方法的对比[J].循证医学,2014,14(02):123-128.

统计推断——正态性检验（图形方法、偏度和峰度、统计（拟合优度）检验）_sm.distributions.ecdf-CSDN博客

https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-test/

https://real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-expanded-test/

? ? ? ?S-W正态性检验法由Shapiro和Wilk1965年提出的，又称W检验。使用原始的S-W检验，在8≤n≤50时可以利用，小样本(n<8)对偏离正态分布的检验不太有效。不幸的是，针对大多数n，统计量W的分布是未知的，必须通过模拟，造表或者近似方法获得。

? ? ? ?而J. P. Royston就是通过近似的方法改进了S-W方法，对样本量的要求为12≤n≤5000，甚至更多；但建议样本量不低于20；该方法被用在了很多软件中（如SAS和SPSS）。

原始版S-W检验，具体步骤如下：

1、将n个样本观测值按由小到大的次序排序。

2、计算S-W正态性检验统计量。

$W=\frac{b^{2}}{SS}=\frac{(\sum_{i=1}^{m}a_{i}(x_{n+1-i}-x_{i}))^{2}}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}$

其中，当n为偶数时，m=n/2；当n为奇数时，m=(n-1)/2。

3、根据给定的检验水平α和样本容量n计算统计量W的临界值 $W_{\alpha}$ 。

4、做出统计判断。若 $W<W_{\alpha}$ ，则认为样本数据所来自的总体不服从正态分布；若 $W>W_{\alpha}$ ，则认为服从正态分布。

上述中的 $a_{i}$ 和 $W_{\alpha}$ 均为查表所得。

excel实现步骤如下：

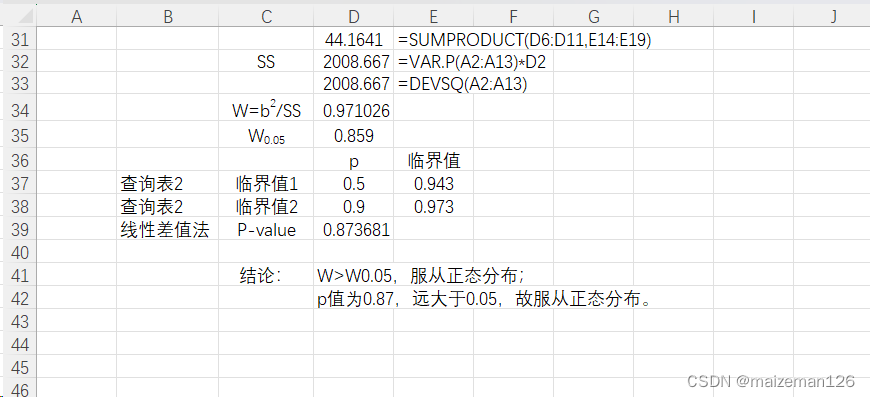
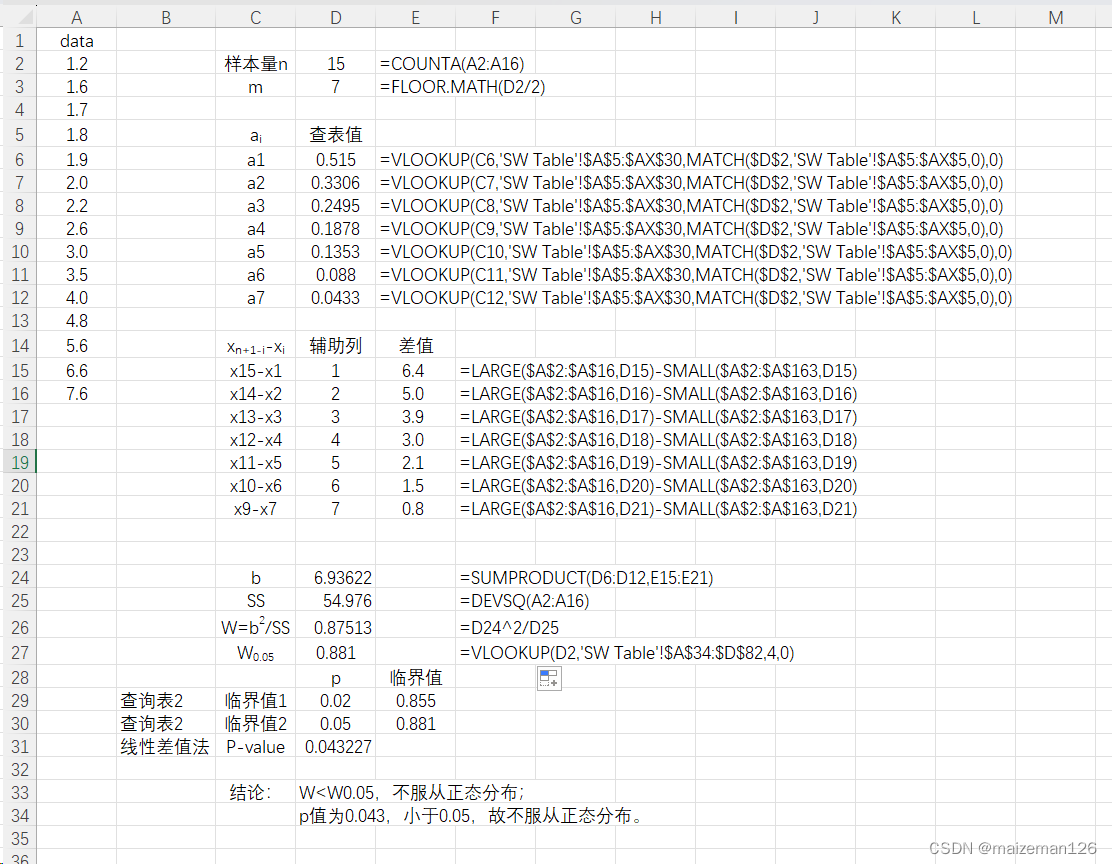
注：已提前将需要查表的信息放到excel中，信息来源参考https://real-statistics.com/statistics-tables/shapiro-wilk-table/

Royston的改进版S-W方法：

1、将n个样本观测值按由小到大的次序排序。

2、利用excel统计分析——Q-Q图_excel 分位数图-CSDN博客中介绍的累计分布函数，取 $CDF=\frac{k-0.375}{n+0.25}$ ，获得n个数据对应累计概率值。

3、利用标准正态分布的概率密度函数的反函数，对得到的CDF进行计算，记作 $m_{i}$ (i=1...n)。

4、对 $m_{i}$ 的平方求和， $m=\sum_{i=1}^{n}m_{i}^{2}$

5、系数 $a_{i}$ ，取 $u=1/\sqrt{n}$ ；

$a_{n}=-2.706056u^{5}+4.434685u^{4}-2.071190u^{3}-0.147981u^{2}+0.221157u+m_{n}m^{-0.5}$

$a_{n-1}=-3.582633u^{5}+5.682633u^{4}-1.752461u^{3}-0.293762u^{2}+0.042981u+m_{n-1}m^{-0.5}$

$a_{i}=m_{i}/\sqrt{\epsilon }$ ?，其中，2<i<n-1， $\epsilon =\frac{m-2m_{n}^{2}-2m_{n-1}^{2}}{1-2a_{n}^{2}-2a_{n-1}^{2}}$

$a_{2}=-a_{n-1}$

$a_{1}=-a_{n}$

系数 $a_{i}$ 之间的关系为： $\sum_{i=1}^{n}a_{i}^{2}=1$

6、计算统计量：

$W=\frac{(\sum_{i=1}^{n}a_{i}x_{i})^2}{\sum_{i=1}^{n}(x_{i}-\bar{x})^2}$

根据W的公式可推算出，W是a与x之间的相关系数的平方，W的取值范围始终在0和1之间。

同样可以根据公式推算出：当n取值在12到5000之间时， $ln(1-W)$ 是近似服从正态分布的，其中μ和σ取值如下：

$\mu =0.0038915(\mathrm{ln } n)^{3}-0.083751(\mathrm{ln } n)^{2}-0.31082\mathrm{ln } n-1.5861$

$\sigma =e^{0.0030302(\mathrm{ln }n)^{2}-0.082676\mathrm{ln }n-0.4803}$

7、W统计量转换为z统计量：

$z=\frac{\mathrm{ln}(1-W)-\mu}{\sigma}$

如果z值对应的p值小于α，则认为不服从正态分布。

excel实现步骤如下：

文章来源:https://blog.csdn.net/maizeman126/article/details/135173662
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！