6种版本的并查集（java实现版）
目录
引入
由孩子指向父亲的这种特殊的树结构可以很高效的处理连接问题，在一个复杂的图中（如下图），给出图中任意两点，问它俩之间是否存在一条连接它俩的路径。
在并查集中，主要有合并集合以及判断是否连接两个动作，即“并”和“查”。
并查集的具体讲解及代码实现
//接口
public interface UF {
//不考虑向并查集中添加元素或者删除元素
int getSize();
//判断是否相连
boolean isConnected(int p, int q);
//两个元素合并在一起，变成一个集合中的元素
void unionElements(int p, int q);
}
Quick Find
相同id值的数字属于同一个集合，如下图，0、2、4、6、8是同一个集合，1、3、5、7、9是同一个集合。
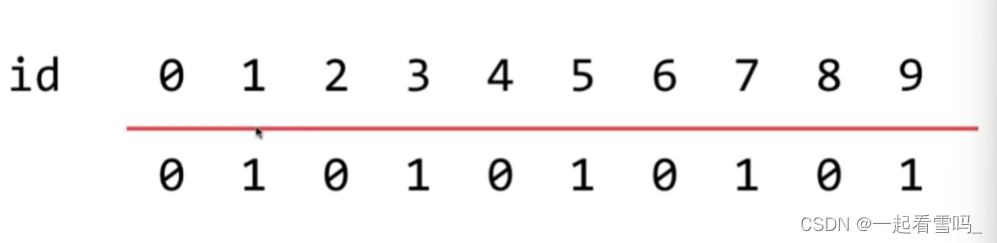
我们用数组存储id值可以很容易的实现isConnected(int p, int q)这个“查”的操作，也就是转换成查找p、q的id值是否相等，即find(p) == find(q)?? 这个find操作的时间复杂度为O(1)，非常快，我们叫做Quick Find。
“查”了解完了，那“并”呢？如果我们想合并1和4又该怎么操作呢。原本1 3 5 7 9是连接起来的，0 2 4 6 8是连接的，一旦我们把1和4连接起来，那么所有和1、4连接的元素也就都连接起来了。在我们上图的例子中我们所有的元素所对应的id值就应该改成一样的，都取0或1，具体都改成0还是都改成1是无所谓的，在这里我们选择都改为1。
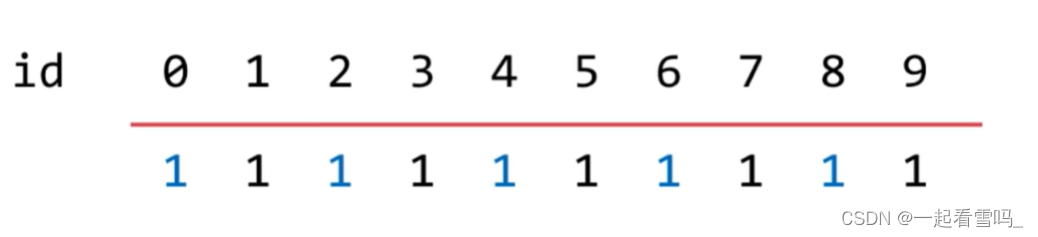
我们通过循环的方式把0都改为1，这个Union的操作时间复杂度为O(n) 。
//第一版的并查集
public class UnionFind1 implements UF{
private int[] id;
public UnionFind1(int size){
id = new int [size];
//每一个元素对应的集合编号都不一样，表示所属不同的集合，各不相连
for(int i = 0; i < id.length; i++){
id[i] = i;
}
}
@Override
public int getSize(){
return id.length;
}
//查找元素p所对应的集合的编号
//由于这个方法不在接口中，所以我们设为private的
private int find(int p){
if(p < 0 || p >= id.length){
throw new IllegalArgumentException("p is out of bound.");
}
return id[p];
}
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
@Override
public void unionElements(int p, int q){
int pID = find(p);
int qID = find(q);
if(pID == qID){
return;
}
for(int i = 0; i < id.length; i++){
if(id[i] == pID){
id[i] = qID;
}
}
}
}
Quick Union
这一版的并查集是一般情况下更常用的。由于Quick Find中的合并操作时间复杂度为O(n)，所以数据规模一大的话算法就会很慢，而下面要讲的这种并查集顾名思义可以很快的合并元素，因为我们要实现一种底层逻辑，即孩子指向父亲的特殊树结构。
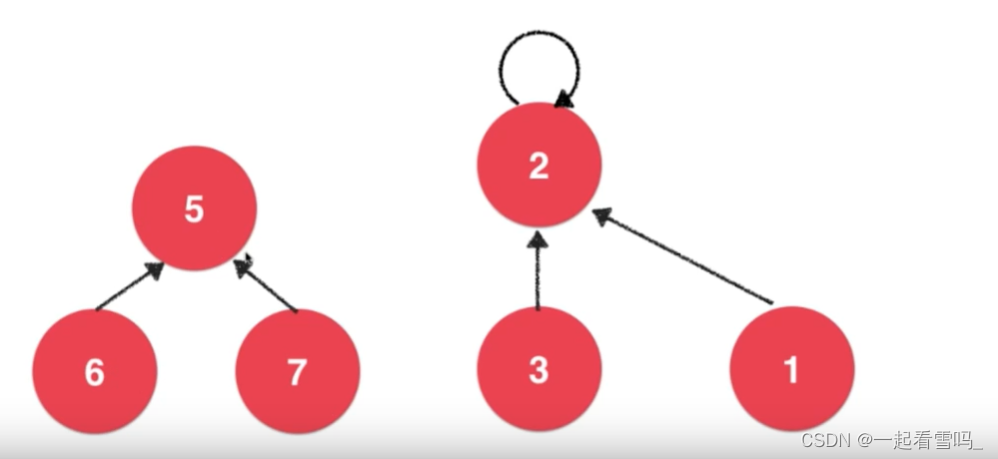
如上图，每个结点只会有一个指针指向另一个结点，结点1、2、3是相连接的，根节点为2，指向它本身。结点5、6、7是相连的，根节点为5，现在我们希望合并3和7，那么只需要将两个集合的根节点相连就好，如下图。?
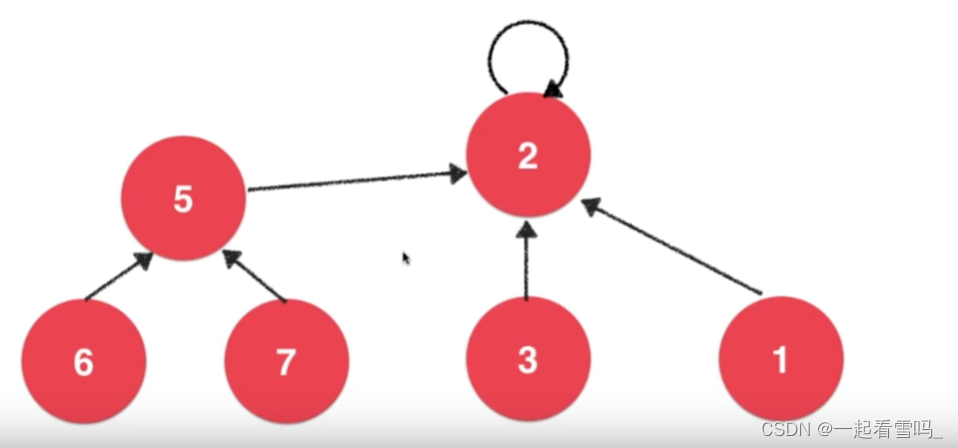
关于指针的存储，我们依然可以采取数组的方式来存储。数组就代表第i个元素的指针指向了某个结点。在初始情况下，每一个结点都是一个根节点，指向自己，没和任意元素相连。此刻不是一个树结构，而是一个森林。
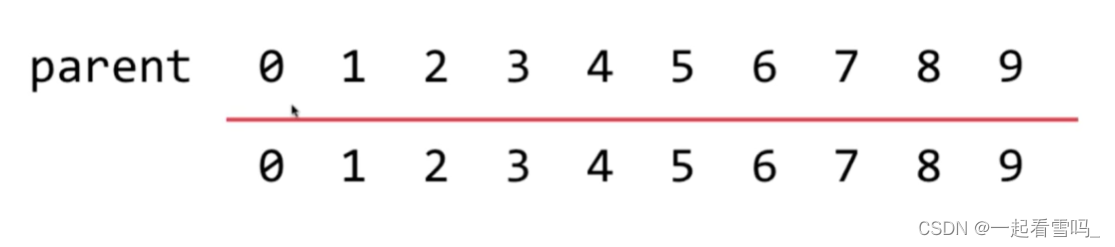
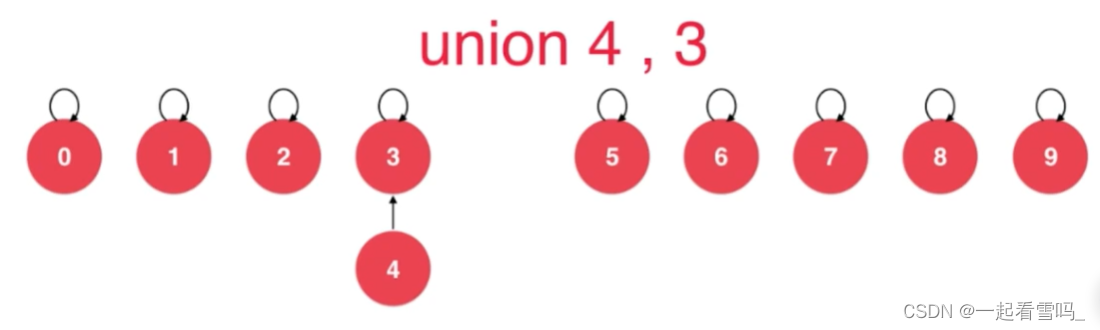
如果我们想合并4、3该怎么做呢？ 很简单，就让4的指针指向3。parent数组中4的位置改为3。
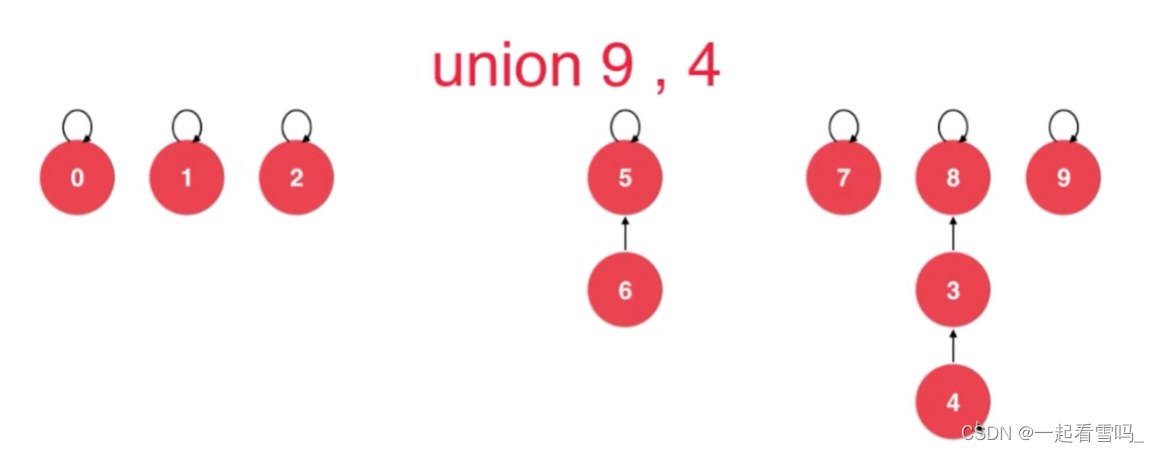
倘若要合并两个树结构中的元素，需要这两个树结构的根节点指向根节点， 这时候就要查找哪个是根节点，即这两棵树中哪个节点是自己指向自己的。比如我们要合并9、4。
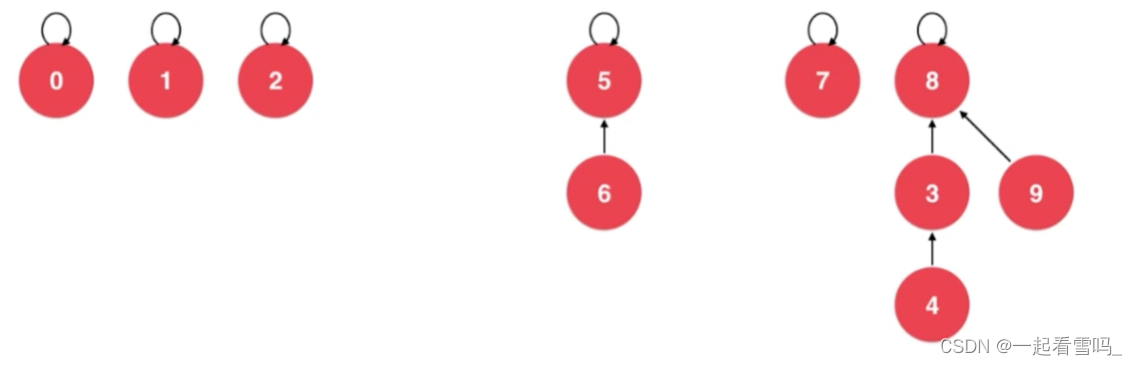我们为什么不让9直接指向4呢？是因为如果那样做就会形成一个链表，我们树结构的优越性就不存在了。?而如果9指向4的根节点，下次我们如果要查询9这个元素所对应的根节点只需要一步查询就好了。（别忘了把parent(9) = 8~）
//第二版并查集
public class UnionFind2 implements UF{
private int[] parent;
public UnionFind2(int size){
parent = new int [size];
for(int i = 0; i < size; i++){
parent[i] = i;
}
}
@Override
public int getSize(){
return parent.length;
}
//时间复杂度为O(h),h是树的高度
//查找到数据所在的树相应的根节点
private int find(int p){
if(p < 0 || p >= parent.length){
throw new IllegalArgumentException("p is out of bound.");
}
while(p != parent[p]){
p = parent[p];
}
return p;
}
//时间复杂度为O(h),h是树的高度
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
//时间复杂度为O(h),h是树的高度
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
parent[pRoot] = qRoot;
}
}
基于size的优化
在某些情况下，我们不判断树的形状就去合并会徒增树的高度形成一个链表的样子(如下图），我们可以考虑当前这棵树有多少个结点，即基于size来解决这个问题。
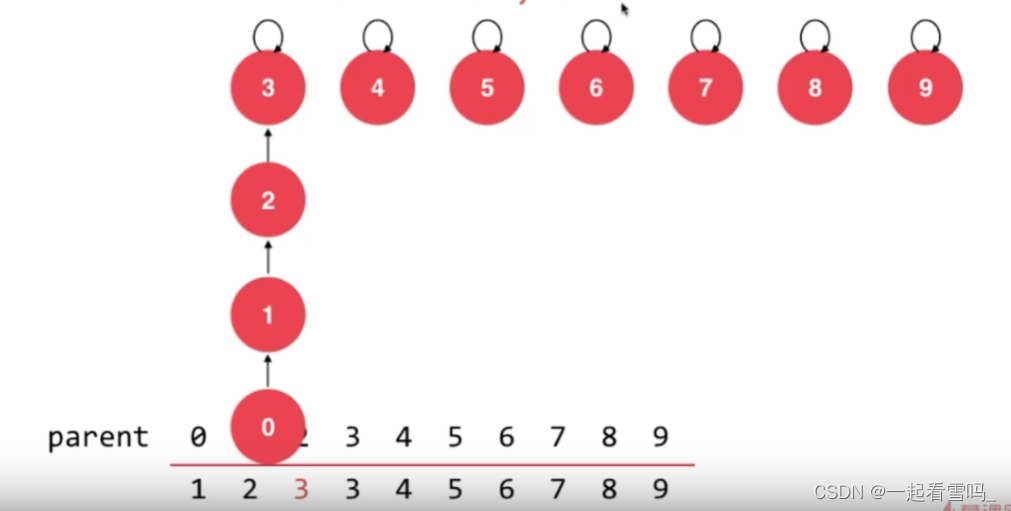
比如，我们要合并4和9。
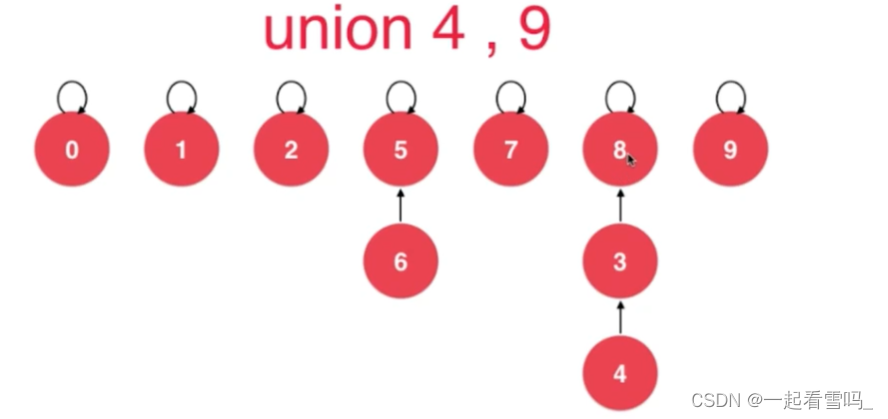
如果我们让8指向9，深度就会为4。?
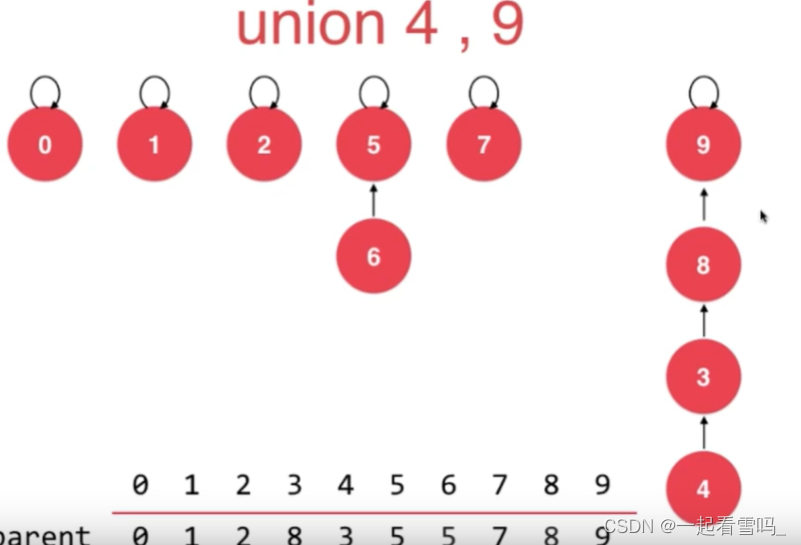
而我们让9指向8的话，树的高度只有3。
即我们让结点个数小的树指向结点个数多的树。
代码实现
//第三版的并查集
public class UnionFind3 implements UF{
private int[] parent;
private int[] sz; //sz[i]表示以i为根的集合中元素个数
public UnionFind3(int size){
parent = new int [size];
sz = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
sz[i] = 1;
}
}
@Override
public int getSize(){
return parent.length;
}
//时间复杂度为O(h),h是树的高度
//查找到数据所在的树相应的根节点
private int find(int p){
if(p < 0 || p >= parent.length){
throw new IllegalArgumentException("p is out of bound.");
}
while(p != parent[p]){
p = parent[p];
}
return p;
}
//时间复杂度为O(h),h是树的高度
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
//时间复杂度为O(h),h是树的高度
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(sz[pRoot] < sz[qRoot]){
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
}
else{
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
}
基于rank的优化
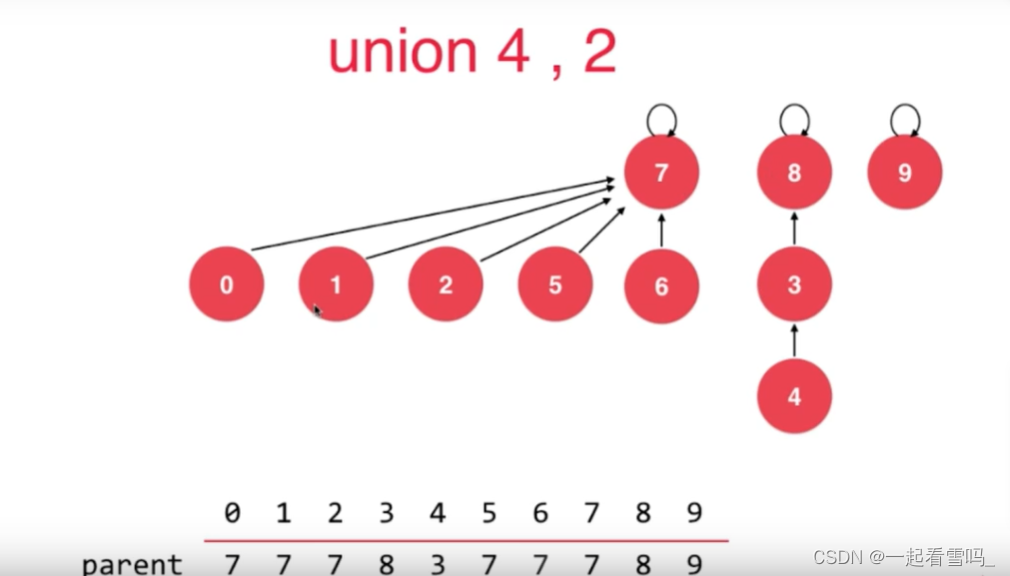
如果是基于size优化的话，结点少的指向结点多的，就会产生下图结果，树的高度变成了4。?
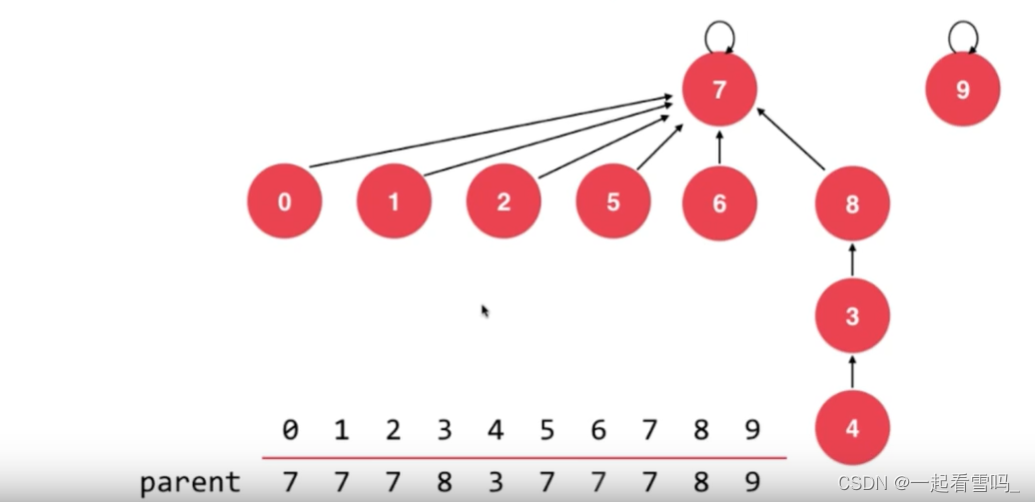
结点数少的树高度反而是高的，结点数多的这棵树高度却只有2。?所以更合理的是让7指向8。
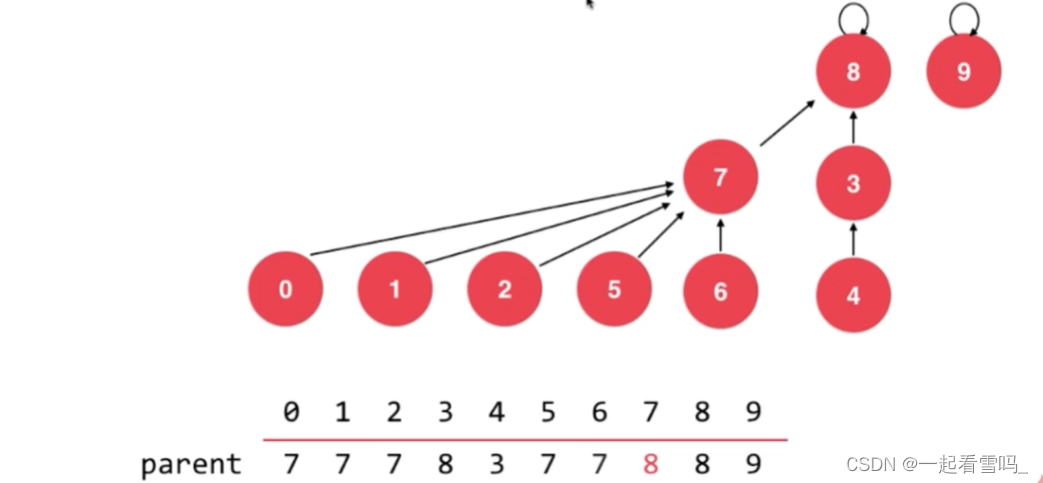
所以更合理的方法是记录一下以这个结点为根的树深度是多少，让深度比较低树指向深度比较高的树，这就是基于rank的优化。
代码实现
//第四版的并查集
public class UnionFind4 implements UF{
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合中树的层数
public UnionFind4(int size){
parent = new int [size];
rank = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize(){
return parent.length;
}
//时间复杂度为O(h),h是树的高度
//查找到数据所在的树相应的根节点
private int find(int p){
if(p < 0 || p >= parent.length){
throw new IllegalArgumentException("p is out of bound.");
}
while(p != parent[p]){
p = parent[p];
}
return p;
}
//时间复杂度为O(h),h是树的高度
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
//时间复杂度为O(h),h是树的高度
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}
else if(rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
//相等时谁指向谁都可以
else{
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}
路径压缩
如上图所示相同效力的三种树，深度不同效率是不同的。路径压缩就是把一棵比较高的树变成比较矮的树。我们把路径压缩放在find方法中，比如我们要查找4的根节点，即find(4)。
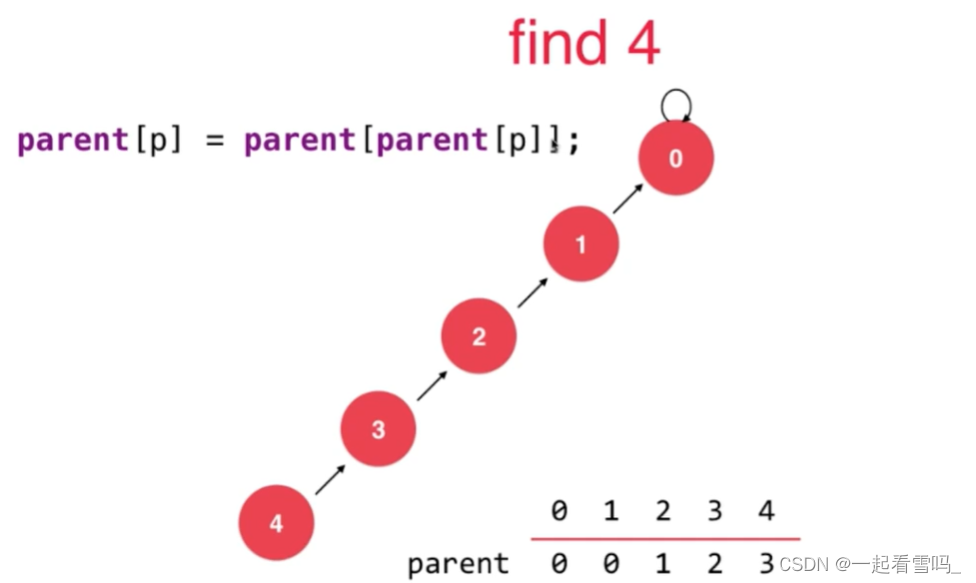
我们可以使用图上那句代码，?即把p结点的父亲的父亲设为p结点的父亲，如下图。树的深度就降低了。
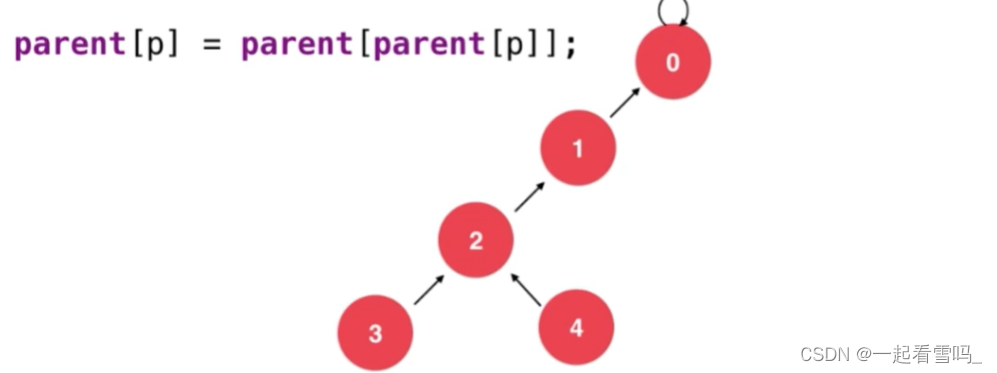
然后我们从2开始，以此类推，得到下图。 把深度从5降成3，这就是路径压缩。
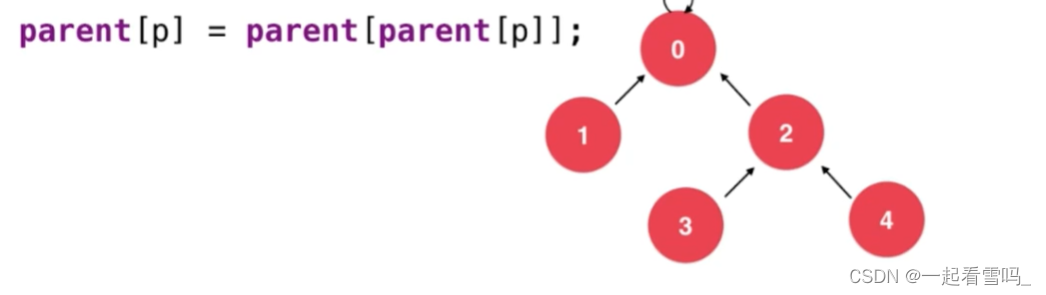
代码实现
//第五版的并查集
public class UnionFind5 implements UF{
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合中树的层数
public UnionFind5(int size){
parent = new int [size];
rank = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize(){
return parent.length;
}
//时间复杂度为O(h),h是树的高度
//查找到数据所在的树相应的根节点
private int find(int p){
if(p < 0 || p >= parent.length){
throw new IllegalArgumentException("p is out of bound.");
}
while(p != parent[p]){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
//时间复杂度为O(h),h是树的高度
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
//时间复杂度为O(h),h是树的高度
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}
else if(rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
//相等时谁指向谁都可以
else{
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}
我们添加上路径压缩后，rank没有跟着维护深度没有问题，rank只是作为合并时的参考，它不作为树的高度值和深度值，这就是为什么它叫rank而不是depth或者length。
更多关于路径压缩的并查集
第六版本主要是为了下图的路径压缩操作一步到位，这样的方式我们要借助递归实现。
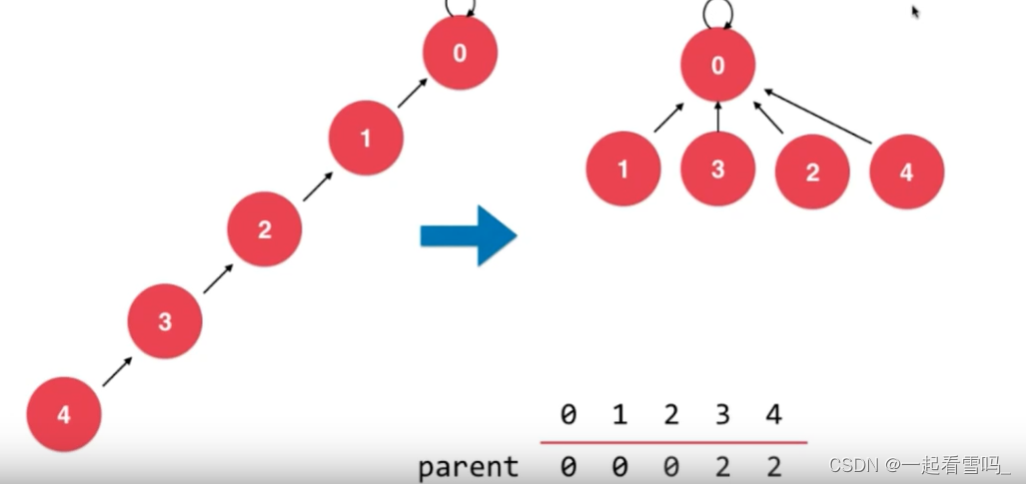
//第六版的并查集
public class UnionFind6 implements UF{
private int[] parent;
private int[] rank; //rank[i]表示以i为根的集合中树的层数
public UnionFind6(int size){
parent = new int [size];
rank = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize(){
return parent.length;
}
//时间复杂度为O(h),h是树的高度
//查找到数据所在的树相应的根节点
private int find(int p){
if(p < 0 || p >= parent.length){
throw new IllegalArgumentException("p is out of bound.");
}
parent[p] = find(parent[p]);
return parent[p];
}
//时间复杂度为O(h),h是树的高度
@Override
public boolean isConnected(int p, int q){
return find(p) == find(q);
}
//时间复杂度为O(h),h是树的高度
@Override
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}
else if(rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
//相等时谁指向谁都可以
else{
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
}
第六版路径压缩比第五版性能上整体差一点点，递归需要额外的消耗，参加算法竞赛不要忘了路径压缩提高性能哦！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- c++ 希尔密码
- 设计模式三(原型模式)
- harmonyOS以修改注释颜色为例 演示如何改变DevEco Studio中指定内容颜色
- 电能质量在线监测装置和防孤岛保护装置光伏并网的应用
- eNSP拓扑建立：静态路由的配置（实验报告）
- 智能优化算法应用：基于卷尾猴算法3D无线传感器网络(WSN)覆盖优化 - 附代码
- Linux中NFS服务器的搭建和安装
- 美易平台：通用电气四季度业绩超预期，展望一季度财务预测
- 统计学-R语言-4.2
- 讲解机器学习中的 K-均值聚类算法及其优缺点。