常用排序算法:插入排序、希尔排序、选择排序、冒泡排序、快速排序、归并排序
插入排序
步骤:
1.从第一个元素开始,该元素可以认为已经被排序
2.取下一个元素tem,从已排序的元素序列从后往前扫描
3.如果该元素大于tem,则将该元素移到下一位
4.重复步骤3,直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面,如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
6.重复步骤2~5
动图演示如下:
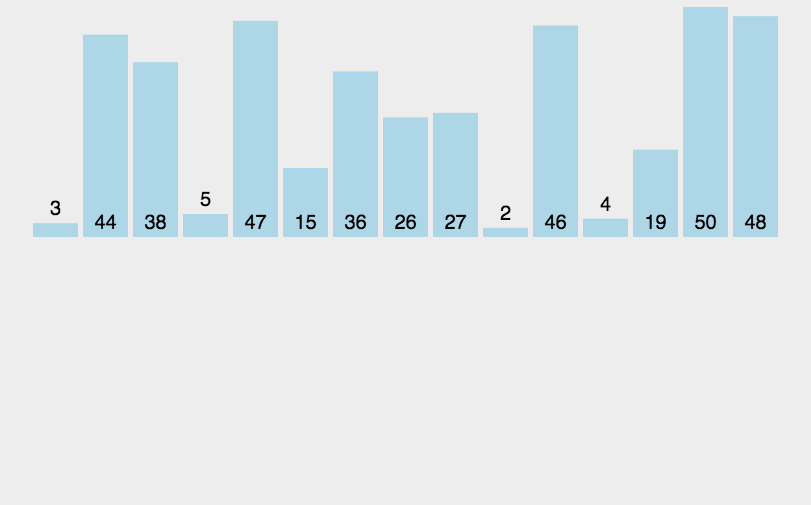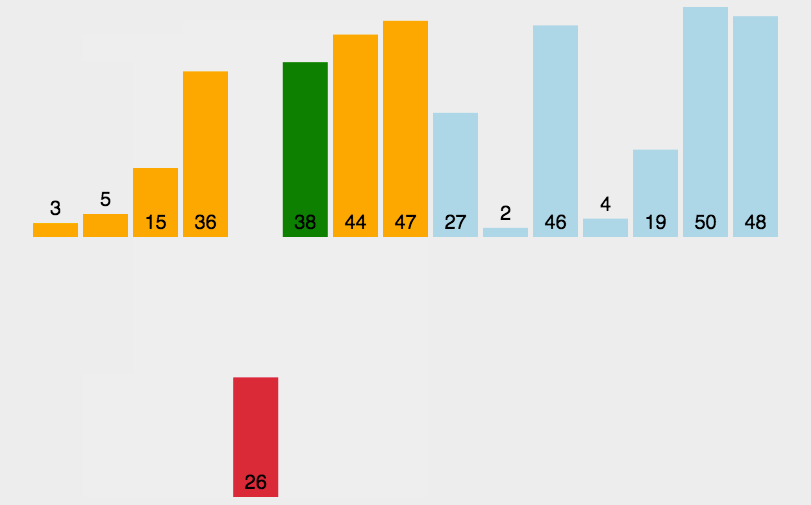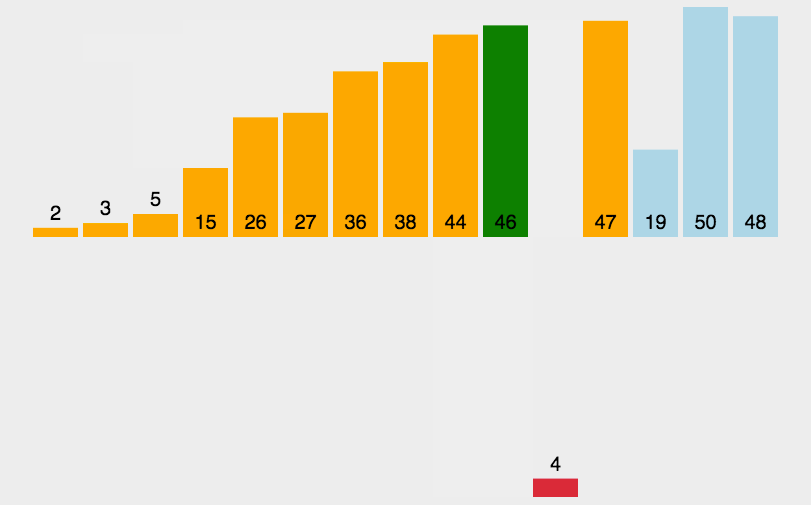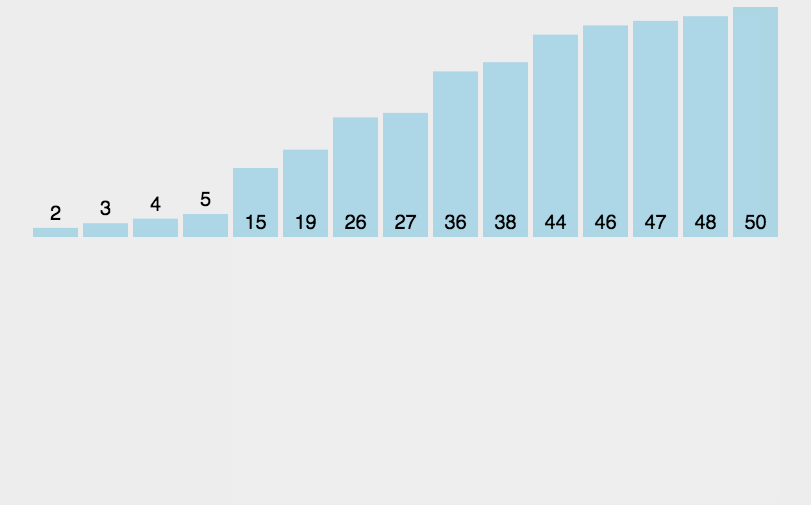
思路:
??在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
??但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。
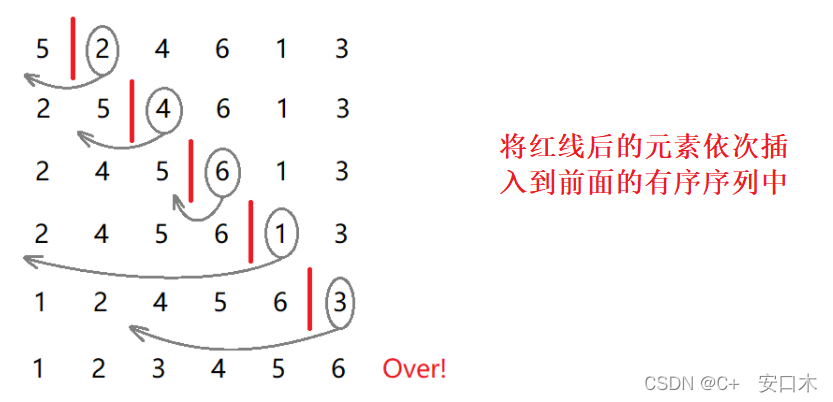
代码如下:
void InsertSort(int* arr, int n)
{
for (int i = 0; i < n - 1; ++i)
{
//记录有序序列最后一个元素的下标
int end = i;
//待插入的元素
int tem = arr[end + 1];
//单趟排
while (end >= 0)
{
//比插入的数大就向后移
if (tem < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
//比插入的数小,跳出循环
else
{
break;
}
}
//tem放到比插入的数小的数的后面
arr[end + 1] = tem;
//代码执行到此位置有两种情况:
//1.待插入元素找到应插入位置(break跳出循环到此)
//2.待插入元素比当前有序序列中的所有元素都小(while循环结束后到此)
}
}
时间复杂度:最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序
??????最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
希尔排序
步骤:
1.先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
2.当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
动图如下:
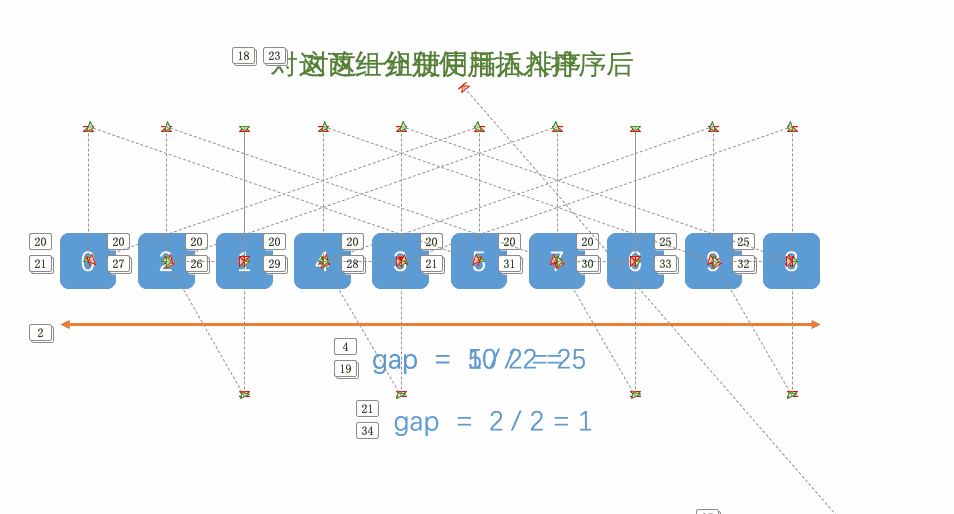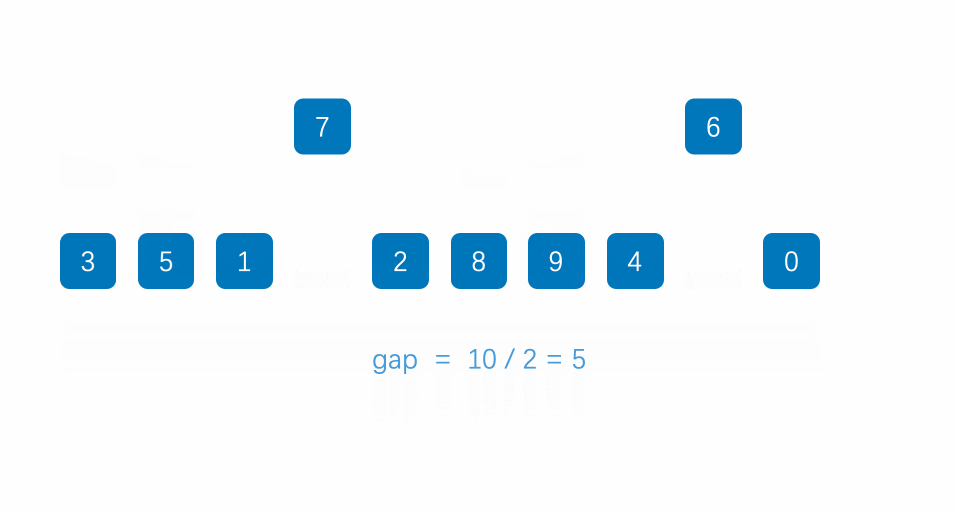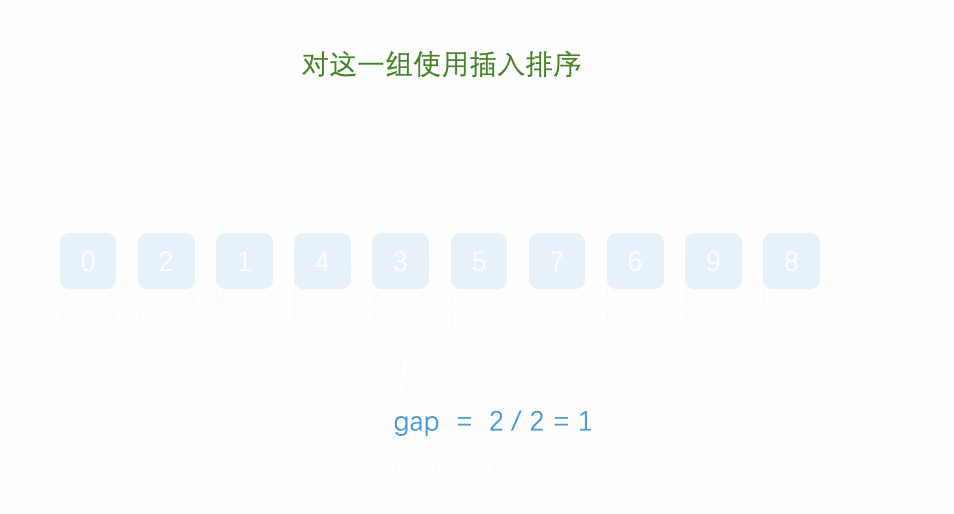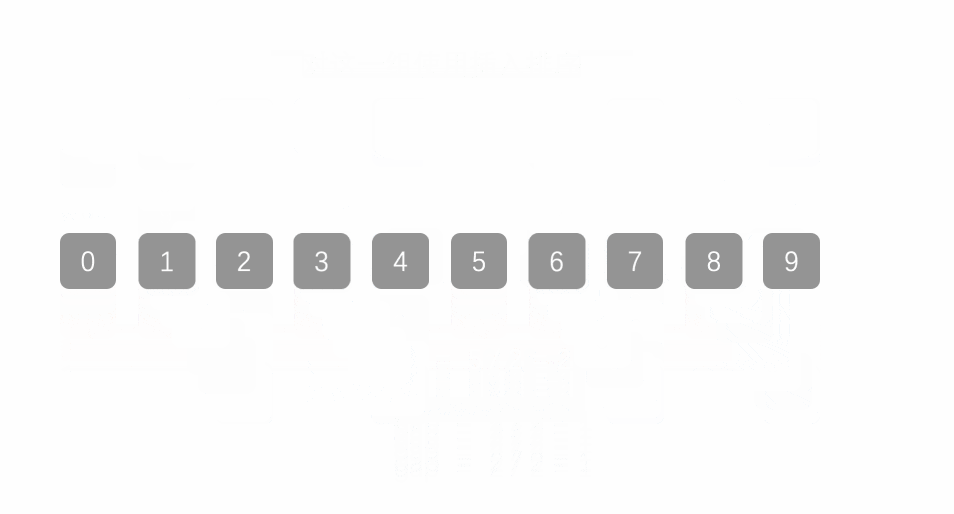
思路:
希尔排序,先将待排序列进行预排序,使待排序列接近有序,然后再对该序列进行一次插入排序,此时插入排序的时间复杂度为O(N),
代码如下:
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap>1)
{
//每次对gap折半操作
gap = gap / 2;
//单趟排序
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tem = arr[end + gap];
while (end >= 0)
{
if (tem < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tem;
}
}
}
时间复杂度平均:O(N^1.3)
空间复杂度:O(1)
选择排序
思路:
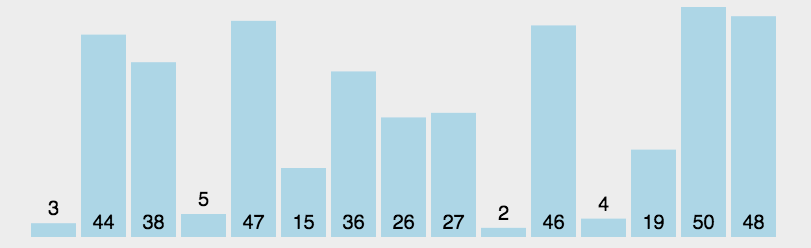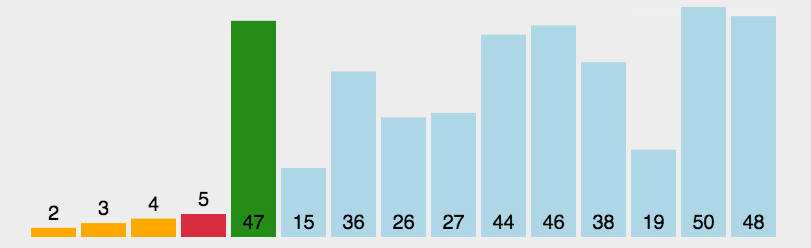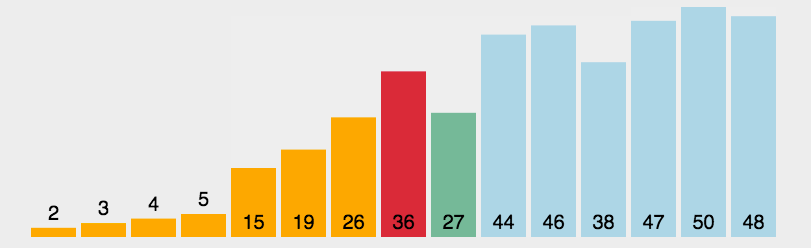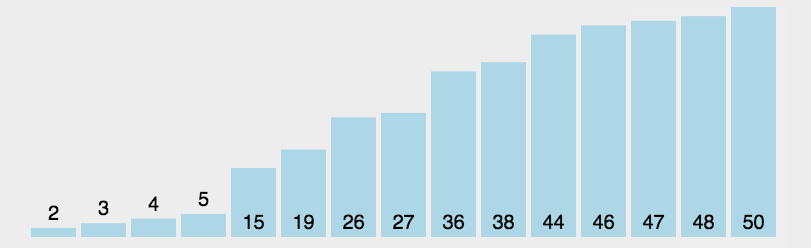
每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
动图如下:
代码如下:
//选择排序
void swap(int* a, int* b)
{
int tem = *a;
*a = *b;
*b = tem;
}
void SelectSort(int* arr, int n)
{
//保存参与单趟排序的第一个数和最后一个数的下标
int begin = 0, end = n - 1;
while (begin < end)
{
//保存最大值的下标
int maxi = begin;
//保存最小值的下标
int mini = begin;
//找出最大值和最小值的下标
for (int i = begin; i <= end; ++i)
{
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
//最小值放在序列开头
swap(&arr[mini], &arr[begin]);
//防止最大的数在begin位置被换走
if (begin == maxi)
{
maxi = mini;
}
//最大值放在序列结尾
swap(&arr[maxi], &arr[end]);
++begin;
--end;
}
}
时间复杂度:最坏情况:O(N^2)
??????最好情况:O(N^2)
空间复杂度:O(1)
冒泡排序
思路:
左边大于右边交换一趟排下来最大的在右边
动图如下:
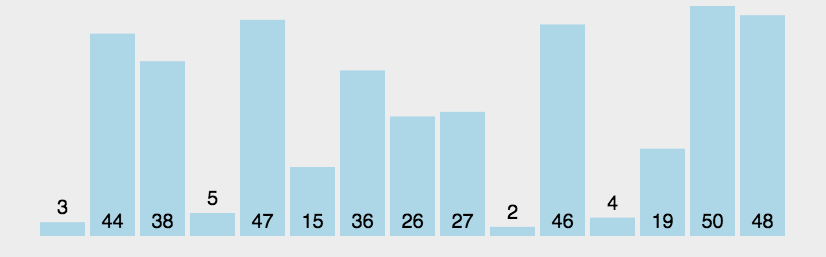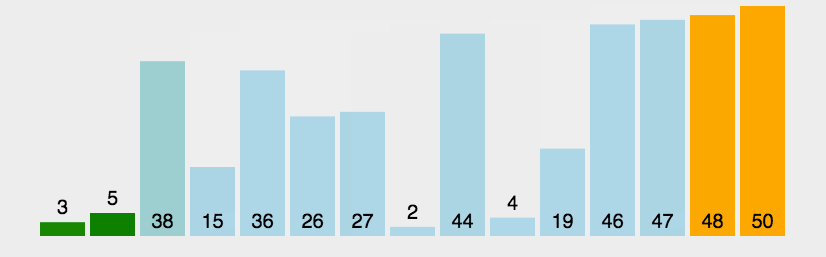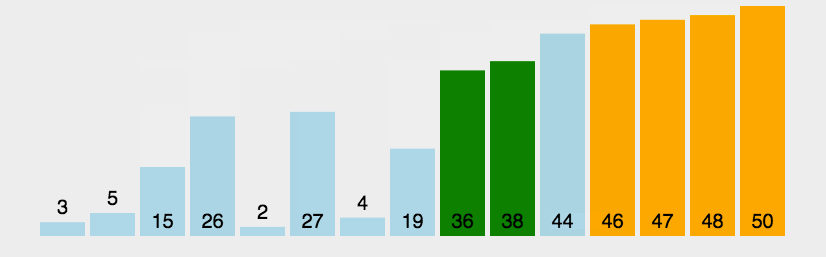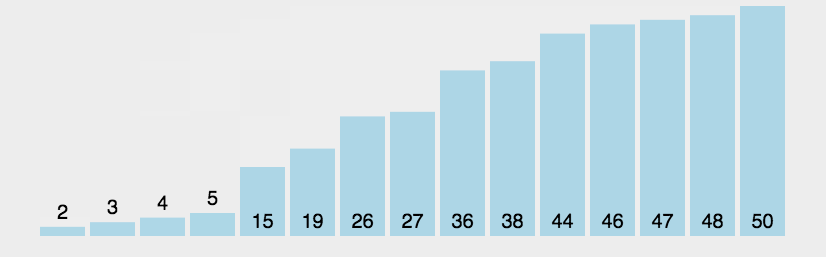
代码如下:
//冒泡排序
void BubbleSort(int* arr, int n)
{
int end = n;
while (end)
{
int flag = 0;
for (int i = 1; i < end; ++i)
{
if (arr[i - 1] > arr[i])
{
int tem = arr[i];
arr[i] = arr[i - 1];
arr[i - 1] = tem;
flag = 1;
}
}
if (flag == 0)
{
break;
}
--end;
}
}
时间复杂度:最坏情况:O(N^2)
??????最好情况:O(N)
空间复杂度:O(1)
快速排序
1、左右指针法
思路:
1、选出一个key,一般是最左边或是最右边的。
2、定义一个begin和一个end,begin从左向右走,end从右向左走。(需要注意的是:若选择最左边的数据作为key,则需要end先走;若选择最右边的数据作为key,则需要bengin先走)。
3、在走的过程中,若end遇到小于key的数,则停下,begin开始走,直到begin遇到一个大于key的数时,将begin和right的内容交换,end再次开始走,如此进行下去,直到begin和end最终相遇,此时将相遇点的内容与key交换即可。(选取最左边的值作为key)
4.此时key的左边都是小于key的数,key的右边都是大于key的数
5.将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作,此时此部分已有序
单趟动图如下:
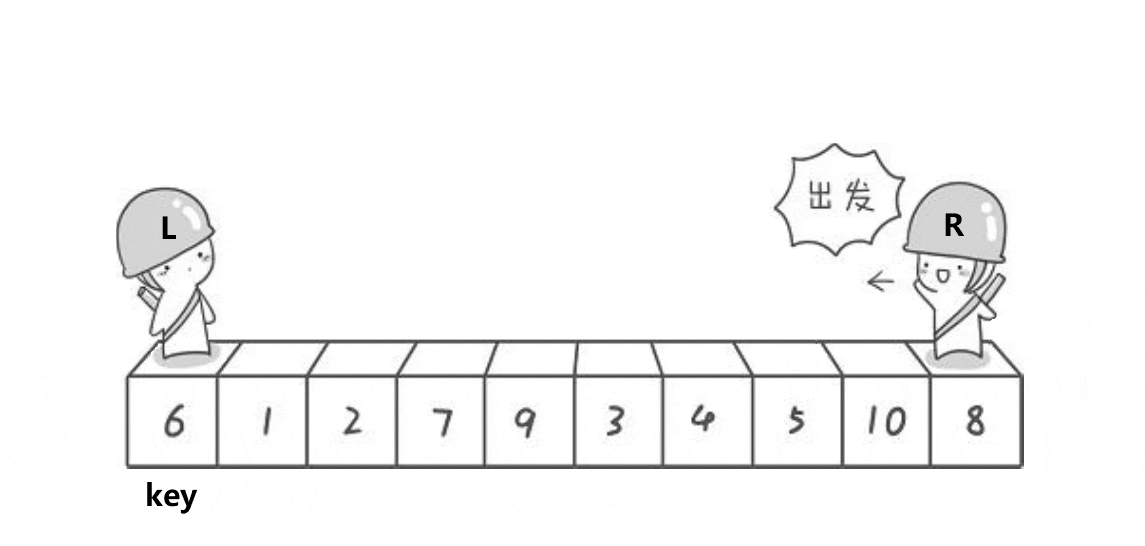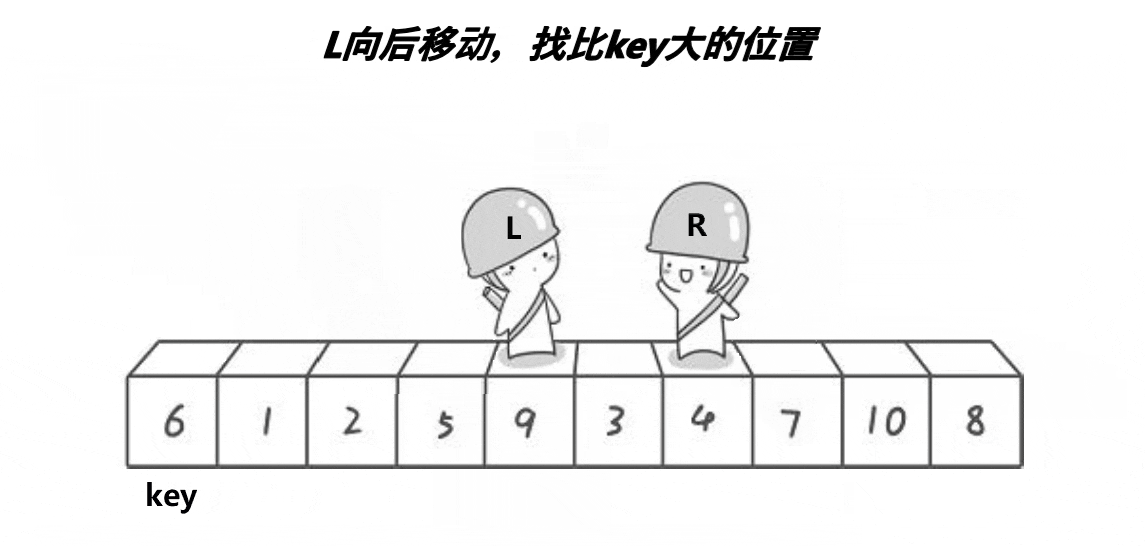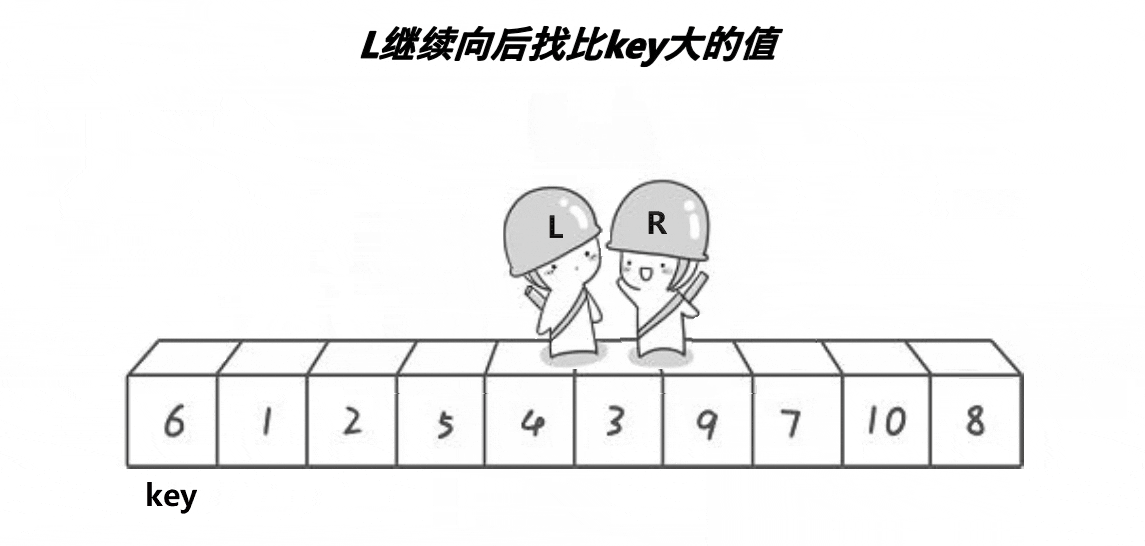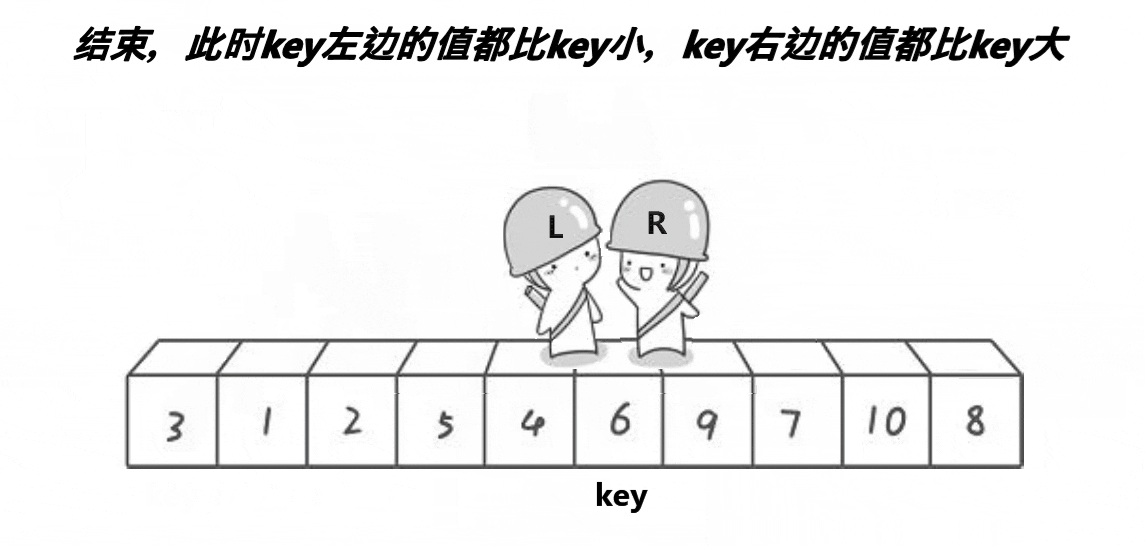
代码如下:
//快速排序 hoare版本(左右指针法)
void QuickSort(int* arr, int begin, int end)
{
//只有一个数或区间不存在
if (begin >= end)
return;
int left = begin;
int right = end;
//选左边为key
int keyi = begin;
while (begin < end)
{
//右边选小 等号防止和key值相等 防止顺序begin和end越界
while (arr[end] >= arr[keyi] && begin < end)
{
--end;
}
//左边选大
while (arr[begin] <= arr[keyi] && begin < end)
{
++begin;
}
//小的换到右边,大的换到左边
swap(&arr[begin], &arr[end]);
}
swap(&arr[keyi], &arr[end]);
keyi = end;
//[left,keyi-1]keyi[keyi+1,right]
QuickSort(arr, left, keyi - 1);
QuickSort(arr,keyi + 1,right);
}
时间复杂度:
在这里插入图片描述
快速排序的过程类似于二叉树其高度为logN,每层约有N个数
挖坑法
2、 递归法
思路:
挖坑法思路与hoare版本(左右指针法)思路类似
1.选出一个数据(一般是最左边或是最右边的)存放在key变量中,在该数据位置形成一个坑
2、还是定义一个L和一个R,L从左向右走,R从右向左走。(若在最左边挖坑,则需要R先走;若在最右边挖坑,则需要L先走)
后面的思路与hoare版本(左右指针法)思路类似在此处就不说了
单趟动图如下:
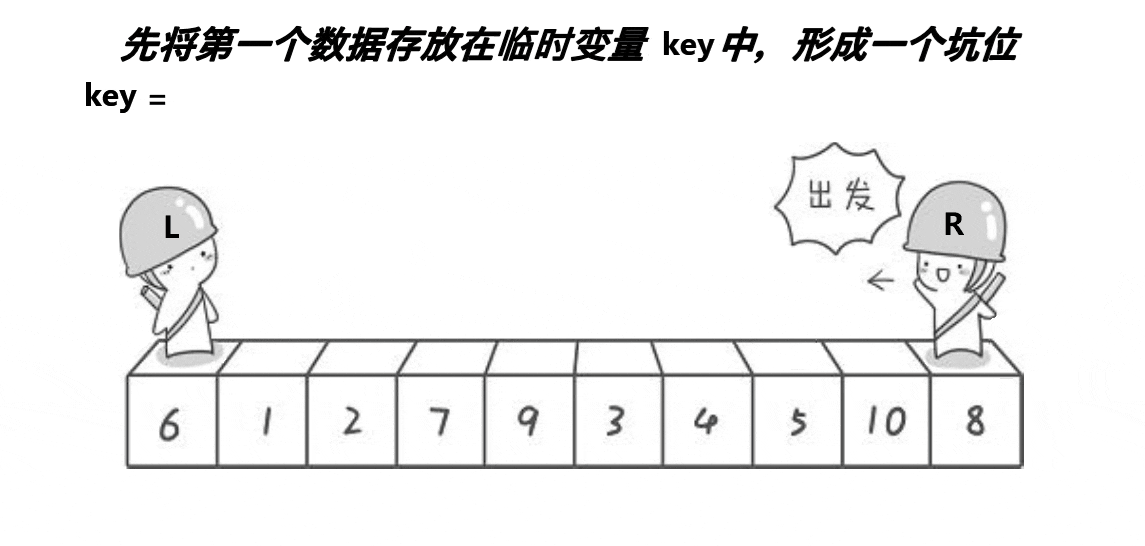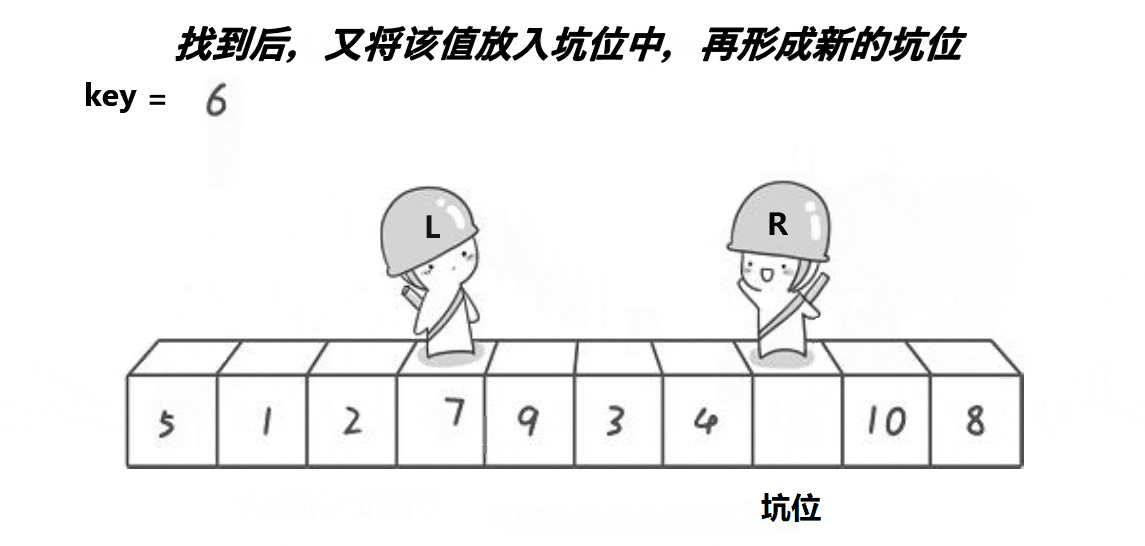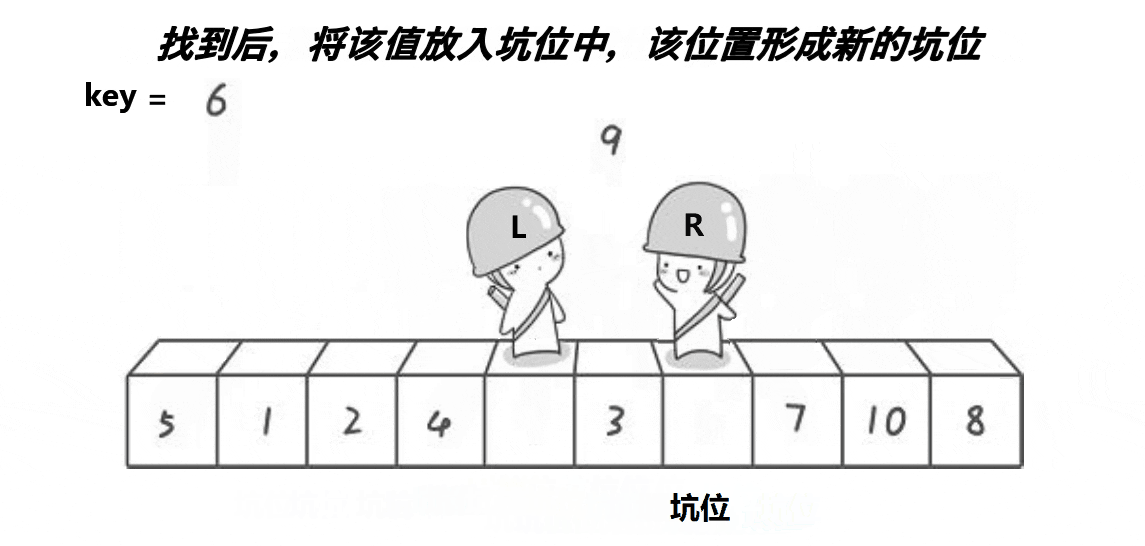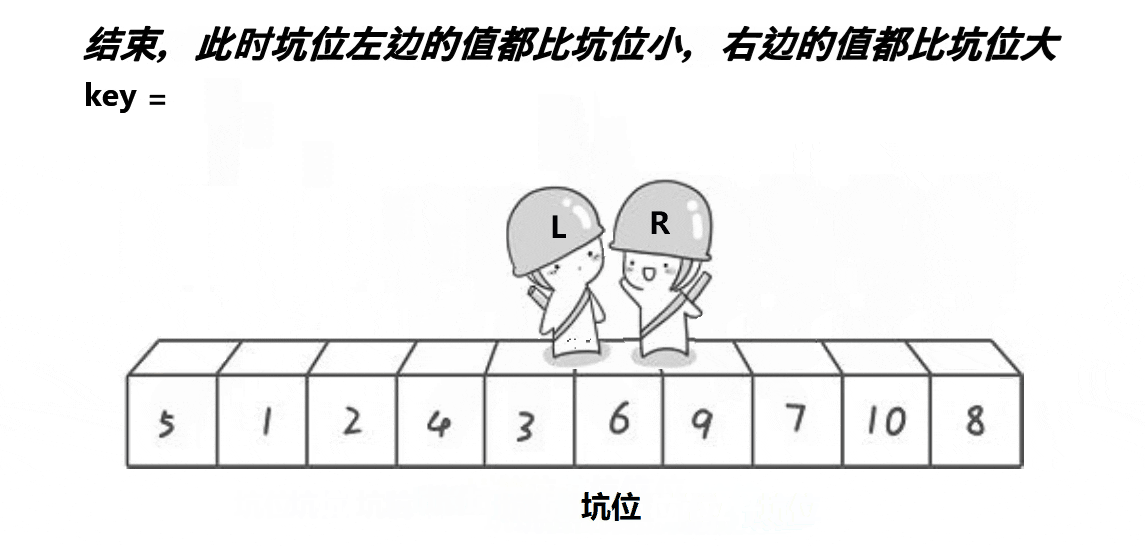
代码:
//快速排序法 挖坑法
void QuickSort1(int* arr, int begin, int end)
{
if (begin >= end)
return;
int left = begin,right = end;
int key = arr[begin];
while (begin < end)
{
//找小
while (arr[end] >= key && begin < end)
{
--end;
}
//小的放到左边的坑里
arr[begin] = arr[end];
//找大
while (arr[begin] <= key && begin < end)
{
++begin;
}
//大的放到右边的坑里
arr[end] = arr[begin];
}
arr[begin] = key;
int keyi = begin;
//[left,keyi-1]keyi[keyi+1,right]
QuickSort1(arr, left, keyi - 1);
QuickSort1(arr, keyi + 1, right);
}
非递归
//单趟排
int PartSort(int* arr, int begin, int end)
{
int key = arr[begin];
while (begin < end)
{
while (key <= arr[end] && begin < end)
{
--end;
}
arr[begin] = arr[end];
while (key >= arr[begin] && begin < end)
{
++begin;
}
arr[end] = arr[begin];
}
arr[begin] = key;
int meeti = begin;
return meeti;
}
void QuickSortNoR(int* arr, int begin, int end)
{
stack<int> st;
//先入右边
st.push(end);
//再入左边
st.push(begin);
while (!st.empty())
{
//左区间
int left = st.top();
st.pop();
//右区间
int right = st.top();
st.pop();
//中间数
int mid = PartSort(arr, left, right);
//当左区间>=mid-1则证明左区间已经排好序了
if (left < mid - 1)
{
st.push(mid - 1);
st.push(left);
}
//当mid+1>=右区间则证明右区间已经排好序
if (right > mid + 1)
{
st.push(right);
st.push(mid + 1);
}
}
}
3、前后指针法
思路:
1、选出一个key,一般是最左边或是最右边的。
2、起始时,prev指针指向序列开头,cur指针指向prev+1。
3、若cur指向的内容小于key,则prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针++;若cur指向的内容大于key,则cur指针直接++。如此进行下去,直到cur到达end位置,此时将key和++prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
然后也还是将key的左序列和右序列再次进行这种单趟排序,如此反复操作下去,直到左右序列只有一个数据,或是左右序列不存在时,便停止操作
//快速排序法 前后指针版本
void QuickSort2(int* arr, int begin, int end)
{
if (begin >= end)
return;
int cur = begin, prev = begin - 1;
int keyi = end;
while (cur != keyi)
{
if (arr[cur] < arr[keyi] && ++prev != cur)
{
swap(&arr[cur], &arr[prev]);
}
++cur;
}
swap(&arr[++prev],&arr[keyi]);
keyi = prev;
//[begin,keyi -1]keyi[keyi+1,end]
QuickSort2(arr, begin, keyi - 1);
QuickSort2(arr, keyi + 1, end);
}
归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法描述
两种方法
- 递归法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
- 迭代法(Bottom-up)
原理如下(假设序列共有n个元素):
- 将序列每相邻两个数字进行归并操作,形成ceil(n/2)个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是1个则将上述序列再次归并,形成ceil(n/4)个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为1
动图演示
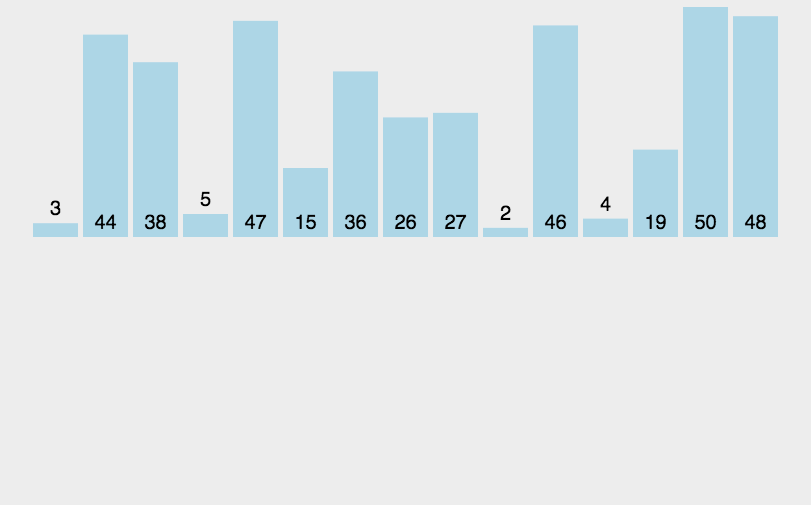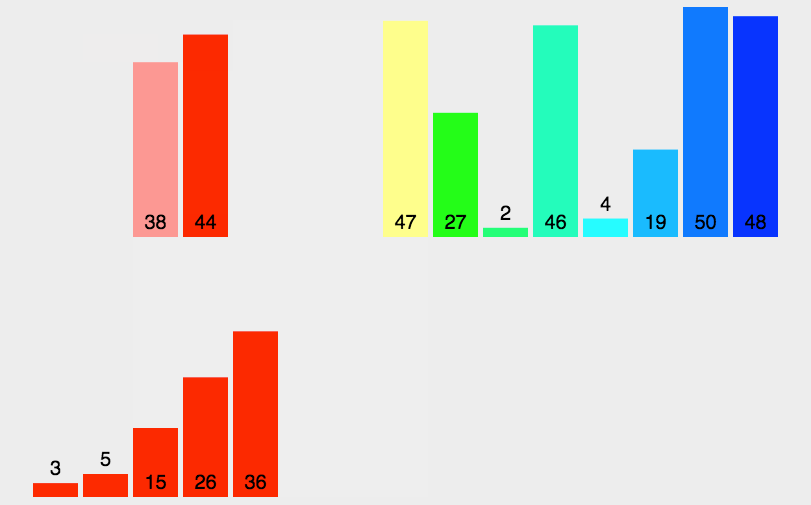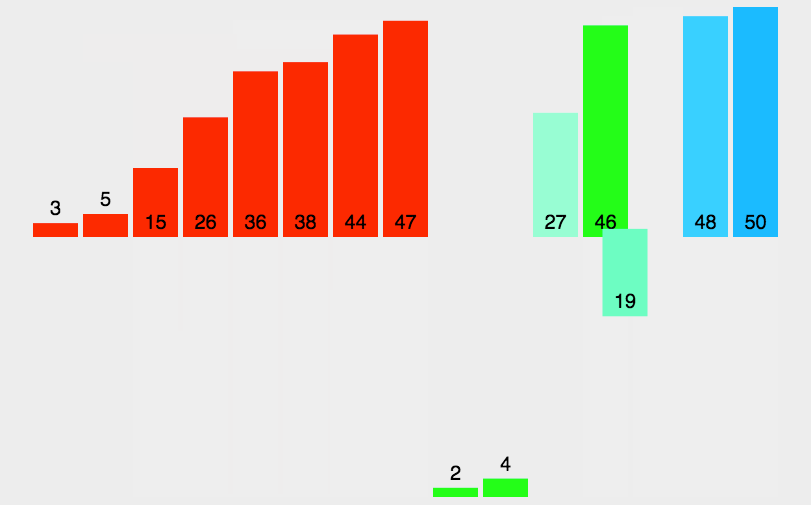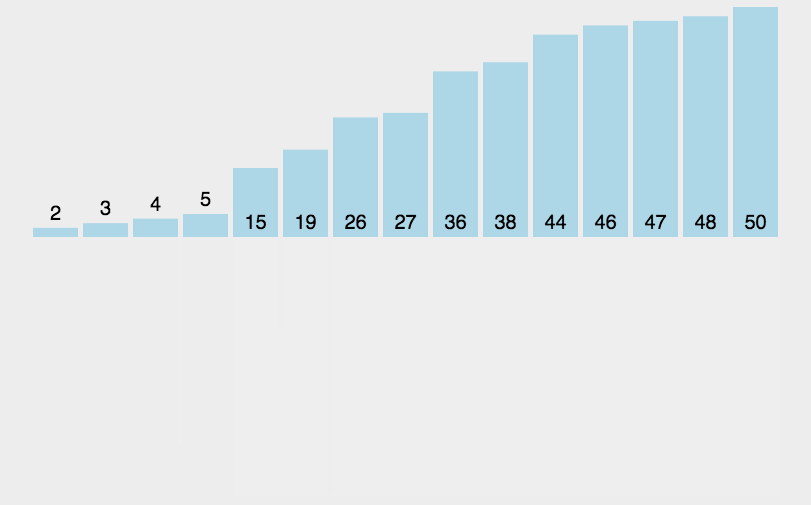
算法实现
public static void mergeSort(int[] arr){
int[] temp =new int[arr.length];
internalMergeSort(arr, temp, 0, arr.length-1);
}
private static void internalMergeSort(int[] arr, int[] temp, int left, int right){
//当left==right的时,已经不需要再划分了
if (left<right){
int middle = (left+right)/2;
internalMergeSort(arr, temp, left, middle); //左子数组
internalMergeSort(arr, temp, middle+1, right); //右子数组
mergeSortedArray(arr, temp, left, middle, right); //合并两个子数组
}
}
// 合并两个有序子序列
private static void mergeSortedArray(int arr[], int temp[], int left, int middle, int right){
int i=left;
int j=middle+1;
int k=0;
while (i<=middle && j<=right){
temp[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
while (i <=middle){
temp[k++] = arr[i++];
}
while ( j<=right){
temp[k++] = arr[j++];
}
//把数据复制回原数组
for (i=0; i<k; ++i){
arr[left+i] = temp[i];
}
}
适用场景
归并排序在数据量比较大的时候也有较为出色的表现(效率上),但是,其空间复杂度O(n)使得在数据量特别大的时候(例如,1千万数据)几乎不可接受。而且,考虑到有的机器内存本身就比较小,因此,采用归并排序一定要注意。
总结:
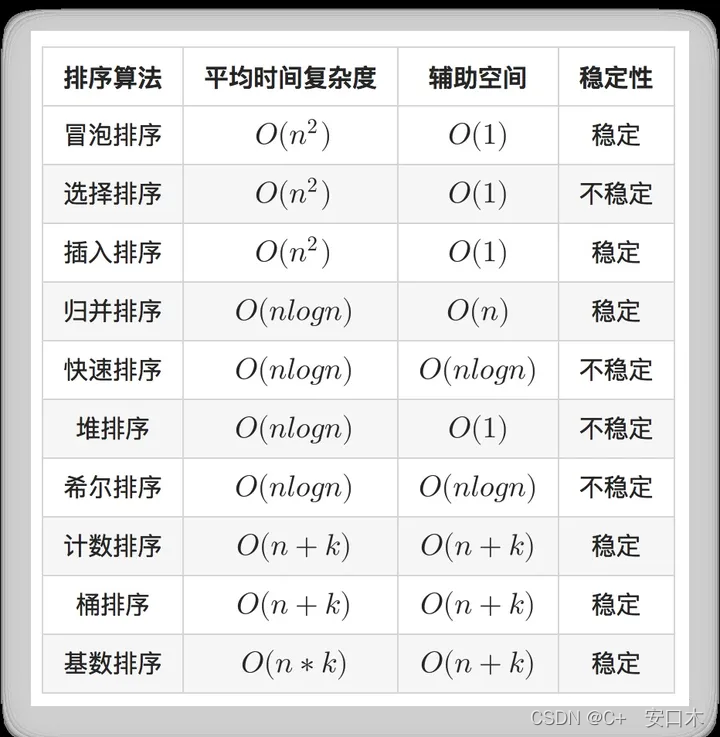
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!