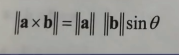TA百人计划学习笔记 1.2.1数学 向量

发布时间：2024年01月12日
  • 源视频 【技术美术百人计划】图形 1.2.1 向量基础_哔哩哔哩_bilibili
  • ppt 1210向量_苗梓(2)
  • 1.撒是向量
    • 定义
      • 有大小和方向的有向线段
      • 没有位置，只有大小和方向
      • 箭头是向量的结束点，尾巴是向量的起始点
      • 描述的位移能被认为是与轴平行的位移序列
      • 表示：三维（ax，ay，az） 二维（ax，ay）
    • 向量与标量
      • 向量：有大小和方向的有向线段
      • 标量：只有大小，没有方向的量
    • 向量与点
      • 向量和点数学形式上相等，但几何意义完全不同
        • 点：有位置，没有实际大小或方向
        • 向量：无位置，有实际大小和方向
        • 联系：任何一个点都可以看作是从原点出发的向量
    • 零向量
      • 唯一大小为零的向量
      • 唯一一个没有方向的量
      • 不是一个点，没有定义某个位置
      • 表示没有位移，类比零标量表示没有数量一样
  • 2.如何计算
    • 标量与向量
      • 定义
        • 不可加
        • 不可减
        • 可乘：将向量的每个分量与标量相乘即可
        • 可除：将向量的每个分量与标量的倒数相乘
        • 几何解释：以标量的大小缩放向量的长度，负值则方向相反
          • 例子
            • -2 *（2，-5）=（-4，10）
            • （6，-2，-4）/ 2 = （3，-1，-2）
      • 向量的模长(大小)
        • 计算公式

        • 几何解释：当我们将所示向量作为斜边构建一个直角三角形，所示向量的大小（模长）即可通过勾股定理推出

      • 标准化向量
        • 标准化向量（单位向量）
          • 大小为1的向量
            • （适用范围：仅需要知道方向而不关心其大小，例如法线）
          • 运算法则：向量除以模长（大小）

    • 向量与向量
      • 向量加减
        • 计算公式（ax，ay）+（bx，by） = （ax+bx，ay+by）
        • 加法：对应位置相加 例：（1，-4）+（7，3）=（8，1）
        • 减法：对应位置相减 例：（-3，6）-（-4，3）=（1，3）
        • 几何解释：
          • 假设有向量（ax，ay）和（bx，by）
          • a向量加b向量=从a向量起点到b向量的结束形成的新的向量
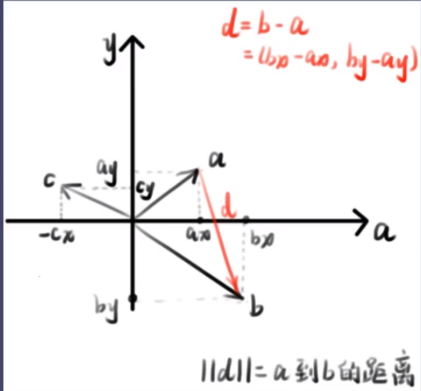
      • 2点间距离
        • 计算公式

        • 应用范围：计算一个向量到另一个向量的距离（a 到 b 的位移向量为 b-a）
        • 几何解释

      • 向量的点积
        • 乘法之点积（又称点乘，内积）
          • 向量点乘就是分量乘积的和
          • 计算公式：（ax，ay）·（bx，by） = ax*bx + ay*by
          • 注意
            • 结果是一个标量
            • 满足乘法交换律
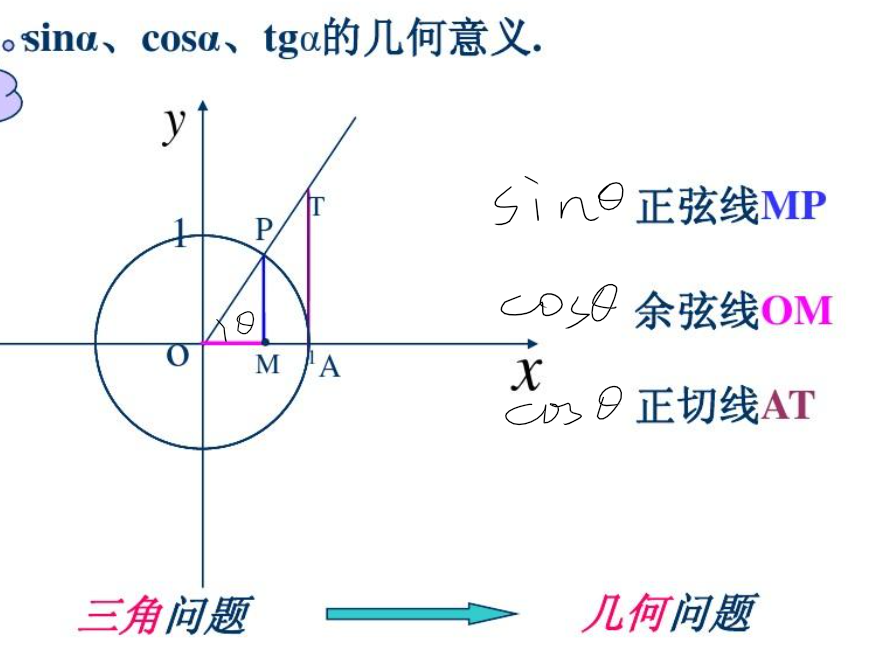
        • 几何意义
          • 几何解释：
            • 点乘描述了两个向量方向的“相似”程度，点乘结果越大，夹角角度越小，两个向量越接近(反馈到渲染上就是面的明暗效果）
          • 计算公式： a · b = |a||b|cosΘ

            • ?

        • 向量的投影
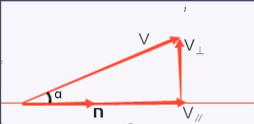
          • 一个向量在另个向量上的投影长度
          • 几何解释：假设有两个向量 V 和 N，将V分解为两个向量， V平行 和 V垂直 ，V平行 平行于 N，V垂直垂直于N，并满足 V = V平行 + V垂直 ，则称平行分量 V平行 为在 N 上的投影

        • 运用

      • 向量的叉积
        • 定义
          • 乘法之叉积（又称叉乘，叉积） 仅运用于3D向量
          • 分量交叉相乘再相减
          • 注意
            • 不满足交换律，a x b ≠ b x a
            • 满足逆交换律：a x b = -（b x a）
        • 计算公式

        • 几何解释：叉乘得到的向量垂直于原来的两个向量
        • 大小与方向判断
          • 大小
            • 计算公式

          • 方向
            • 左右手坐标系
文章来源:https://blog.csdn.net/weixin_57856130/article/details/135457041
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章