DDPM推导笔记
各位佬看文章之前，可以先去看看这个视频，并给这位up主点赞投币，这位佬讲解的太好了：大白话AI
1.前置知识的学习
1.1 正态分布特性
? （1）正态分布的概率密度函数
f
(
x
)
=
1
2
π
σ
e
?
(
x
?
μ
)
2
2
σ
2
,
记为
N
(
μ
,
σ
2
)
f(x) = {1 \over \sqrt{2 \pi } \sigma} e^{-{{(x-\mu)^2} \over {2 \sigma^2}}} ,记为N(\mu, \sigma^2)
f(x)=2π?σ1?e?2σ2(x?μ)2?,记为N(μ,σ2)
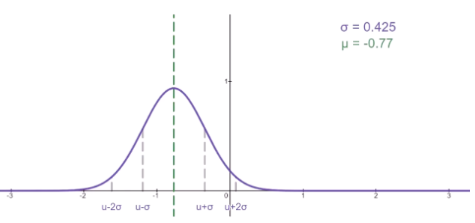
? 当 μ = 0 , σ 2 = 1 \mu = 0, \sigma^2=1 μ=0,σ2=1时，则记为标准正态分布，记为 N ( 0 , 1 ) N(0, 1) N(0,1), 又称为高斯分布。
? （2）正态分布的基本性质
N
(
μ
1
,
σ
1
2
)
+
N
(
μ
2
,
σ
2
2
)
=
N
(
μ
1
+
μ
2
,
σ
1
2
+
σ
2
2
)
a
?
N
(
μ
,
σ
)
=
N
(
a
?
μ
,
(
a
?
σ
)
2
)
N(\mu_1, \sigma_1^2) + N(\mu_2, \sigma_2^2) = N(\mu_1+\mu2, \sigma_1^2+\sigma_2^2) \\ a*N(\mu, \sigma) = N(a*\mu, (a*\sigma)^2)
N(μ1?,σ12?)+N(μ2?,σ22?)=N(μ1?+μ2,σ12?+σ22?)a?N(μ,σ)=N(a?μ,(a?σ)2)
1.2 贝叶斯定理
?
A
,
B
A, B
A,B是两个随机事件，
P
(
A
)
P(A)
P(A)表示
事件
A
事件A
事件A发生的概率，
P
(
B
∣
A
)
P(B|A)
P(B∣A)表示A事件发生的情况下B事件发生的概率，则贝叶斯定理如下：
P
(
A
∣
B
)
=
P
(
B
∣
A
)
?
P
(
A
)
P
(
B
)
P(A|B) = {{P(B|A) * P(A)} \over P(B)}
P(A∣B)=P(B)P(B∣A)?P(A)?
2. 前向过程（加噪）
? 如图所示，前向过程则是一个加载过程，在每个时间步，都从正态分布中随机采样一个和图片等大的噪声（也可以理解为噪声图片），则加噪过程：
x
1
=
β
1
?
?
1
+
1
?
β
1
?
x
0
x_1 = \sqrt{\beta_1} * \epsilon_1 + \sqrt{1-\beta_1} * x_0
x1?=β1????1?+1?β1???x0?
? 其中
x
0
x_0
x0?表示原始图片，
?
1
\epsilon_1
?1? 表示随机噪声，
β
1
\beta_1
β1?表示扩散速度，
T
T
T表示扩散的次数，则可以一次推导：
x
1
=
β
1
?
?
1
+
1
?
β
1
?
x
0
x
2
=
β
2
?
?
2
+
1
?
β
2
?
x
1
x
3
=
β
3
?
?
3
+
1
?
β
3
?
x
2
?
?
?
?
?
?
x
T
=
β
T
?
?
T
+
1
?
β
T
?
x
T
?
1
前后关系就可以记为：
x
t
=
β
t
?
?
t
+
1
?
β
t
?
x
t
?
1
x_1 = \sqrt{\beta_1} * \epsilon_1 + \sqrt{1-\beta_1} * x_0 \\ x_2 = \sqrt{\beta_2} * \epsilon_2 + \sqrt{1-\beta_2} * x_1 \\ x_3 = \sqrt{\beta_3} * \epsilon_3 + \sqrt{1-\beta_3} * x_2 \\ ······ \\ x_T = \sqrt{\beta_T} * \epsilon_T + \sqrt{1-\beta_T} * x_{T-1} \\ 前后关系就可以记为： \\ x_t = \sqrt{\beta_t} * \epsilon_t + \sqrt{1-\beta_t} * x_{t-1} \\
x1?=β1????1?+1?β1???x0?x2?=β2????2?+1?β2???x1?x3?=β3????3?+1?β3???x2???????xT?=βT????T?+1?βT???xT?1?前后关系就可以记为：xt?=βt????t?+1?βt???xt?1?
? 为简化后续运算，令
α
t
=
1
?
β
t
\alpha_t = 1 - \beta_t
αt?=1?βt?, 则有：
x
t
=
1
?
α
t
?
?
t
+
α
t
?
x
t
?
1
x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1}
xt?=1?αt????t?+αt???xt?1?
? 思考：如何能更快的得到
x
T
x_T
xT?？因为如果加噪1000步，岂不是要计算1000次上述的运算！好的，下面介绍怎样依赖正态分布的可加性来简化运算，从而推导出
x
0
x_0
x0?到
x
t
x_t
xt?的关系：
由：
x
t
=
1
?
α
t
?
?
t
+
α
t
?
x
t
?
1
x
t
?
1
=
1
?
α
t
?
1
?
?
t
?
1
+
α
t
?
1
?
x
t
?
2
把
x
t
?
1
代入到
x
t
中可以推导出：
x
t
=
1
?
α
t
?
?
t
+
α
t
?
(
1
?
α
t
?
1
?
?
t
?
1
+
α
t
?
1
?
x
t
?
2
)
=
a
t
(
1
?
a
t
?
1
)
?
?
t
?
1
+
1
?
a
t
?
?
t
+
a
t
a
t
?
1
?
x
t
?
2
其中：
?
t
?
1
和
?
t
是两个随机噪声，且两者是两个独立的随机变量。
打个比喻：我们有一个骰子掷两次分别得到
?
t
?
1
和
?
t
，完全可以等效
于我们有两个骰子掷一次。即：一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布，所以
,
如果我们知道两个骰子掷一次的概率分布，然后进行一次采样即可。
由： \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1} \\ x_{t-1} = \sqrt{1- \alpha_{t-1}} * \epsilon_{t-1} + \sqrt{\alpha_{t-1}} * x_{t-2} \\ 把x_{t-1}代入到x_t中可以推导出： \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * (\sqrt{1- \alpha_{t-1}} * \epsilon_{t-1} + \sqrt{\alpha_{t-1}} * x_{t-2}) \\ = \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} + \sqrt{1-a_t} * \epsilon_t + \sqrt{a_t a_{t-1}} * x_{t-2} \\ 其中：\epsilon_{t-1} 和 \epsilon_{t} 是两个随机噪声，且两者是两个独立的随机变量。\\ 打个比喻：我们有一个骰子掷两次分别得到\epsilon_{t-1} 和 \epsilon_{t}，完全可以等效\\ 于我们有两个骰子掷一次。即：一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布，所以,\\ 如果我们知道两个骰子掷一次的概率分布，然后进行一次采样即可。 \\
由：xt?=1?αt????t?+αt???xt?1?xt?1?=1?αt?1????t?1?+αt?1???xt?2?把xt?1?代入到xt?中可以推导出：xt?=1?αt????t?+αt???(1?αt?1????t?1?+αt?1???xt?2?)=at?(1?at?1?)???t?1?+1?at????t?+at?at?1???xt?2?其中：?t?1?和?t?是两个随机噪声，且两者是两个独立的随机变量。打个比喻：我们有一个骰子掷两次分别得到?t?1?和?t?，完全可以等效于我们有两个骰子掷一次。即：一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布，所以,如果我们知道两个骰子掷一次的概率分布，然后进行一次采样即可。
由正态分布的基本性质可知： ? t 和 ? t ? 1 服从 N ( 0 , 1 ) , 即： ? t ～ N ( 0 , 1 ) , ? t ? 1 ～ N ( 0 , 1 ) 可以推导出： 1 ? a t ? ? t ～ N ( 0 , 1 ? α t ) a t ( 1 ? a t ? 1 ) ? ? t ? 1 ～ N ( 0 , a t ? a t ? a t ? 1 ) ) 由正态分布的基本性质可知：\\ \epsilon_t和\epsilon_{t-1}服从N(0, 1),即：\epsilon_t \sim N(0,1), \epsilon_{t-1} \sim N(0,1) \\ 可以推导出： \sqrt{1-a_t} * \epsilon_t \sim N(0, 1- \alpha_t) \\ \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} \sim N(0, a_t-a_t*a_{t-1})) 由正态分布的基本性质可知：?t?和?t?1?服从N(0,1),即：?t?～N(0,1),?t?1?～N(0,1)可以推导出：1?at????t?～N(0,1?αt?)at?(1?at?1?)???t?1?～N(0,at??at??at?1?))
从而推导出： a t ( 1 ? a t ? 1 ) ? ? t ? 1 + 1 ? a t ? ? t ～ N ( 0 , 1 ? a t ? a t ? 1 ) 从而推导出： \\ \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} + \sqrt{1-a_t} * \epsilon_t \sim N(0, 1-a_t*a_{t-1}) 从而推导出：at?(1?at?1?)???t?1?+1?at????t?～N(0,1?at??at?1?)
进而推导出： x t = 1 ? a t ? a t ? 1 ? ? + a t ? a t ? 1 ? x t ? 2 , 其中： ? ～ N ( 0 , 1 ? a t ? a t ? 1 ) 进而推导出：\\ x_t = \sqrt{1-a_t*a_{t-1}} * \epsilon + \sqrt{a_t*a_{t-1}}*x_{t-2}, 其中：\epsilon \sim N(0, 1-a_t*a_{t-1}) 进而推导出：xt?=1?at??at?1????+at??at?1???xt?2?,其中：?～N(0,1?at??at?1?)
这里就可到了 x t 和 x t ? 2 之间的关系，然后依靠上面的方法就可以一次推导出 x t 到 x 0 的关系 ( 数学归纳法证明 ) ，具体如下： x t = 1 ? a t a t ? 1 a t ? 2 . . . a 1 ? ? + a t a t ? 1 a t ? 2 . . . a 1 ? x 0 其中， ? ～ N ( 0 , 1 ? a t a t ? 1 a t ? 2 . . . a 1 ) 这里就可到了x_t和x_{t-2}之间的关系，然后依靠上面的方法就可以一次推导出x_t到x_0的关系(数学归纳法证明)，具体如下： \\ x_t = \sqrt{1 - a_ta_{t-1}a_{t-2}...a_1} * \epsilon + \sqrt{a_ta_{t-1}a_{t-2}...a1} * x_0 \\ 其中，\epsilon \sim N(0, 1 - a_ta_{t-1}a_{t-2}...a_1) 这里就可到了xt?和xt?2?之间的关系，然后依靠上面的方法就可以一次推导出xt?到x0?的关系(数学归纳法证明)，具体如下：xt?=1?at?at?1?at?2?...a1????+at?at?1?at?2?...a1??x0?其中，?～N(0,1?at?at?1?at?2?...a1?)
为了方便表示 , 记： a ˉ t = a t a t ? 1 a t ? 2 . . . a 1 则： x t = 1 ? a ˉ t ? ? + a ˉ t x 0 为了方便表示,记： \bar{a}_t = a_ta_{t-1}a_{t-2}...a_1 \\ 则： x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 为了方便表示,记：aˉt?=at?at?1?at?2?...a1?则：xt?=1?aˉt????+aˉt??x0?
? 至此，前向过程就记录完成了，我们得到 x 0 到 x t x_0到x_t x0?到xt?的关系，并且可以只通过一次采样就能得到。
3. 反向过程（去噪）
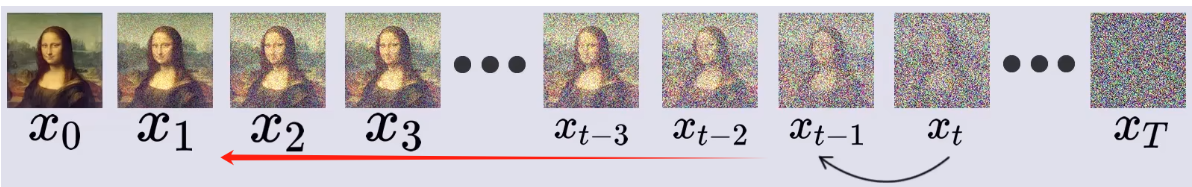
? 去噪过程就是从
x
T
x_T
xT?一步步反推回
x
0
x_0
x0?。
3.1 反向原理推导
? 由贝叶斯定理：
P
(
A
∣
B
)
=
P
(
B
∣
A
)
?
P
(
A
)
P
(
B
)
P(A|B) = {{P(B|A) * P(A)} \over P(B)}
P(A∣B)=P(B)P(B∣A)?P(A)?
? 我们可以令：
由于
x
t
到
x
t
?
1
是一个随机过程，则令：
P
(
x
t
?
1
∣
x
t
)
:
表示在给定
x
t
的情况下，
x
t
?
1
的概率。
套用贝叶斯定理得：
P
(
x
t
?
1
∣
x
t
)
=
P
(
x
t
∣
x
t
?
1
)
?
P
(
x
t
?
1
)
P
(
x
t
)
其中，
P
(
x
t
)
和
P
(
x
t
?
1
)
分别表示
x
t
和
t
t
?
1
的概率
,
也就是从
x
0
原图得到它们的概率。
由于x_t到x_{t-1}是一个随机过程，则令： \\ P(x_{t-1}|x_t): 表示在给定x_t的情况下，x_{t-1}的概率。 \\ 套用贝叶斯定理得： \\ P(x_{t-1} | x_t) = { P(x_t | x_{t-1}) * P(x_{t-1}) \over P(x_t)} \\ 其中，P(x_t)和P(x_{t-1})分别表示x_t和t_{t-1}的概率,也就是从x_0原图得到它们的概率。
由于xt?到xt?1?是一个随机过程，则令：P(xt?1?∣xt?):表示在给定xt?的情况下，xt?1?的概率。套用贝叶斯定理得：P(xt?1?∣xt?)=P(xt?)P(xt?∣xt?1?)?P(xt?1?)?其中，P(xt?)和P(xt?1?)分别表示xt?和tt?1?的概率,也就是从x0?原图得到它们的概率。
所以，可以在每个式子后面添加一个先验
x
0
,
即：
P
(
x
t
?
1
∣
x
t
,
x
0
)
=
P
(
x
t
∣
x
t
?
1
,
x
0
)
?
P
(
x
t
?
1
∣
x
0
)
P
(
x
t
∣
x
0
)
所以，可以在每个式子后面添加一个先验x0,即： \\ P(x_{t-1} | x_t,x_0) = { P(x_t | x_{t-1},x_0) * P(x_{t-1} | x_0) \over P(x_t | x_0)} \\
所以，可以在每个式子后面添加一个先验x0,即：P(xt?1?∣xt?,x0?)=P(xt?∣x0?)P(xt?∣xt?1?,x0?)?P(xt?1?∣x0?)?
有：
P
(
x
t
∣
x
t
?
1
,
x
0
)
给定
x
t
?
1
到
x
t
的概率。
前向过程中可知：
x
t
=
1
?
α
t
?
?
t
+
α
t
?
x
t
?
1
x
t
=
1
?
a
ˉ
t
?
?
+
a
ˉ
t
x
0
?
t
和
?
分别服从
N
(
0
,
1
)
从而推导出：
x
t
～
N
(
a
t
x
t
?
1
,
1
?
a
t
)
或：
x
t
～
N
(
a
ˉ
t
x
0
,
1
?
a
ˉ
t
)
以及：
x
t
?
1
～
N
(
a
ˉ
t
?
1
x
0
,
1
?
a
ˉ
t
?
1
)
有： \\ P(x_t|x_{t-1}, x_0) 给定x_{t-1}到x_t的概率。 \\ 前向过程中可知： \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1} \\ x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 \\ \epsilon_t和\epsilon分别服从N(0, 1) \\ 从而推导出： \\ x_t \sim N(\sqrt{a_t} x_{t-1}, 1-a_t) \\ 或： \\ x_t \sim N(\sqrt{\bar{a}_t} x_0, 1-\bar{a}_t) \\ 以及： \\ x_{t-1} \sim N(\sqrt{\bar{a}_{t-1}} x_0, 1-\bar{a}_{t-1}) \\
有：P(xt?∣xt?1?,x0?)给定xt?1?到xt?的概率。前向过程中可知：xt?=1?αt????t?+αt???xt?1?xt?=1?aˉt????+aˉt??x0??t?和?分别服从N(0,1)从而推导出：xt?～N(at??xt?1?,1?at?)或：xt?～N(aˉt??x0?,1?aˉt?)以及：xt?1?～N(aˉt?1??x0?,1?aˉt?1?)
? 然后就可以把他们分别写成概率密度形式：
? 然后将概率密度函数带入到贝叶斯定理中，就可以得到：
? 化简成高斯分布得：
? P ( x t ? 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt?1?∣xt?,x0?) =
? 由此推导出：
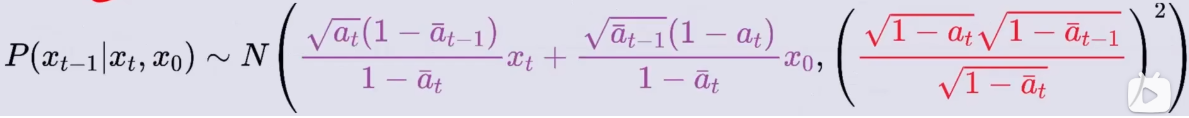
我们的目的是通过
x
t
求出
x
t
?
1
,
然后由
x
t
?
1
推导出
x
t
?
2
?
?
?
直到求出
x
0
，
但现在的式子中出现了
x
0
,
怎么办？
没关系，我们之前由
x
t
和
x
0
的关系：
x
t
=
1
?
a
ˉ
t
?
?
+
a
ˉ
t
x
0
我们的目的是通过x_t求出x_{t-1},然后由x_{t-1}推导出x_{t-2}···直到求出x_0，\\ 但现在的式子中出现了x_0,怎么办？ \\ 没关系，我们之前由x_t和x_0的关系： \\ x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 \\
我们的目的是通过xt?求出xt?1?,然后由xt?1?推导出xt?2????直到求出x0?，但现在的式子中出现了x0?,怎么办？没关系，我们之前由xt?和x0?的关系：xt?=1?aˉt????+aˉt??x0?
? 变换可以得到：
? 将它带入到
P
(
x
t
?
1
∣
x
t
,
x
0
)
P(x_{t-1}|x_t, x_0)
P(xt?1?∣xt?,x0?)的概率密度函数中可得：
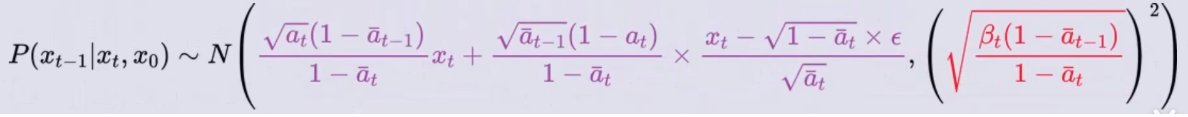
? 它表示的是：对于任意
x
t
x_t
xt?的图像都可以用
x
0
x_0
x0?加载而来；而只要知道了从
x
0
x_0
x0?到
x
t
x_t
xt?加入的噪声
?
\epsilon
?，就能得到它前一时刻
x
t
?
1
x_{t-1}
xt?1?的概率分布，即：
P
(
x
t
?
1
∣
x
t
,
x
0
)
P(x_{t-1}|x_t, x_0)
P(xt?1?∣xt?,x0?) 。
? 这里我们就需要使用神经网络，输入 x t x_t xt?时刻的图像，预测此图像相对于某个 x 0 x_0 x0?原图加入的噪声 ? \epsilon ?。
? 如图所示，也就是说：
?
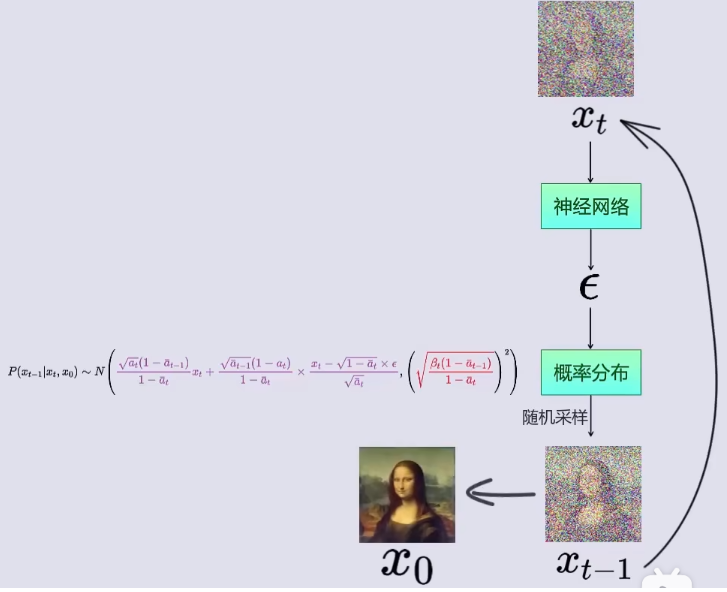
Step1: 在神经网络中，输入
x
t
x_t
xt?时刻图像，训练得到此图像相对于某个
x
0
x_0
x0?原图加入的噪声
?
\epsilon
?。
? Step2： 将噪声 ? \epsilon ?带入到 x t ? 1 x_{t-1} xt?1?的概率密度函数 P ( x t ? 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt?1?∣xt?,x0?)中；
? Step3: 从 x t ? 1 x_{t-1} xt?1?的概率密度函数 P ( x t ? 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt?1?∣xt?,x0?)中随机采样，得到 x t ? 1 x_{t-1} xt?1?(即t-1时刻对应的图像)；
? Step4: 将 x t ? 1 x_{t-1} xt?1?作为神经网络的输入，带入到Step1中，循环Step1 ~ Step3，知道得到 x 0 x_0 x0?
? DDPM中的神经网络选用的UNet.
? 至此，结束！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- DevOps(11)
- 代码随想录算法训练营第十三天 |二叉树递归遍历、非递归遍历、统一非递归
- 一文了解什么是微信小程序
- 5G随身WiFi都是骗人的？5G随身WiFi靠谱品牌推荐，哪个5G随身WiFi最好用
- 市场复盘总结 20240113
- P2383 狗哥玩木棒 约翰玩木棒
- OCP NVME SSD规范解读-5.命令超时限制
- hyper-v ubuntu2204指定静态ip地址
- Java的异常
- Shell三剑客：awk（awk编辑编程）五