运筹说 第67期 | 动态规划模型的建立与求解

通过前一期的学习，我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。

动态规划模型的建立

一?概述

建立动态规划的模型，就是分析问题并建立问题的动态规划基本方程。

成功地应用动态规划方法的关键，在于识别问题的多阶段特征，将问题分解成为可用递推关系式联系起来的若干子问题，而正确建立基本递推关系方程的关键又在于正确选择状态变量，保证各阶段的状态变量具有递推的状态转移关系

二?例题展示

接下来小编将以资源分配问题为例介绍动态规划的建模条件及解法，详见例1。资源分配问题是动态规划的典型应用之一，资源可以是资金、原材料、设备、劳力等，资源分配就是将一定数量的一种或几种资源恰当地分配给若干使用者，以获取最大效益。

例1：某公司有资金10万元，若投资于项目的投资额为时，其收益分别为，问应如何分配投资数额才能使总收益最大?

首先这是一个与时间无明显关系的静态最优化问题，可列出其静态模型：

求，使，且满足约束

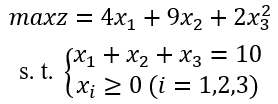
为了应用动态规划方法求解，可以人为地赋予它“时段”的概念。将投资项目排序，依次对项目1、2、3投资，即把问题划分为3个阶段，每个阶段只决定对一个项目应投资的金额，从而转化为一个3段决策过程。通常可以把决策变量定为原静态问题中的变量 ?，即设

状态变量和决策变量有密切关系，状态变量一般为累计量或随递推过程变化的量。针对本例，可以把每阶段可供使用的资金定为状态变量，初始状态。为可分配用于第一种项目的最大资金，则当第一阶段（k=1）时，有

第二阶段（k=2）时，状态变量为余下可投资于其余两个项目的资金，即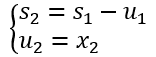

一般地，当第k段时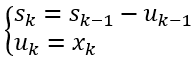

于是有

阶段k：本例中取1，2，3。

状态变量：第k段可以投资于第k项到第3个项目的资金。

决策变量 ：决定给第k个项目投资的资金。

状态转移方程：

指标函数：

最优指标函数 ：当可投资金为时，投资第k-3项所得的最大收益。

基本方程为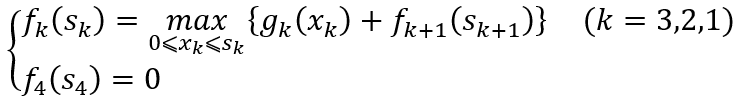

用动态规划方法逐段求解，便可得到各项目最佳投资金额， 就是所求的最大收益。

三 模型建立要点

1.分析题意，识别问题的多阶段特性，按时间或空间的先后顺序适当地划分为满足递推关系的若干阶段，对非时序的静态问题要人为地赋予“时段”概念。

2.正确地选择状态变量，使其具备两个必要特征：

（1）可知性；即过程演变的各阶段状态变量的取值，能直接或间接地确定。

（2）能够确切地描述过程的演变且满足无后效性。即由第阶段的状态出发的后部子过程，可以看作是一个以为初始状态的独立过程。

3.根据状态变量与决策变量的含义，正确写出状态转移方程或转移规则。

4.根据题意明确指标函数 ，最优指标函数 以及阶段指标 的含义，并正确列出最优指标函数的递推关系及边界条件（即基本方程）。

逆序解法与顺序解法

动态规划的求解有两种基本方法：逆序解法（后向动态规划方法）、顺序解法（前向动态规划方法）。

上一期的例题求解实际使用的就是逆序解法，即寻优的方向与多阶段决策过程的实际行进方向相反，从最后一段开始计算逐段前推，求得全过程的最优策略。与之相反，顺序解法的寻优方向与过程的行进方向相同，计算时从第一段开始逐段向后递推，计算后一阶段要用到前一阶段的求优结果，最后一段计算的结果就是全过程的最优结果。

一 例题展示

小编接下来将用例2来说明顺序解法。

例2：给定一个线路网格图（图1），要从A地向F地铺设一条输油管道，各点间连线上的数字表示距离，问应该选择什么路线，可使总距离最短？

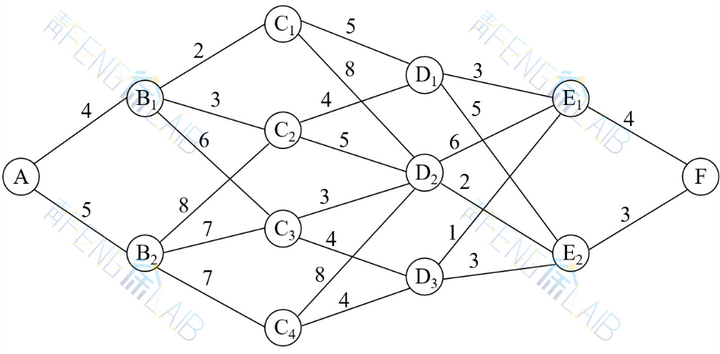
图1

由于此问题的始点A与终点F都是固定的，计算由A点到F点的最短路线与由F点到A点的最短路线没有什么不同。若设表示从起点A到第k阶段状态的最短距离，我们就可以由前向后逐步求出起点A到各阶段起点的最短距离，最后求出A点到F点的最短距离及路径。计算步骤如下：

k=0时，，这是边界条件。

k=1时，按的定义有

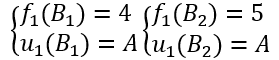
k=2时，

?

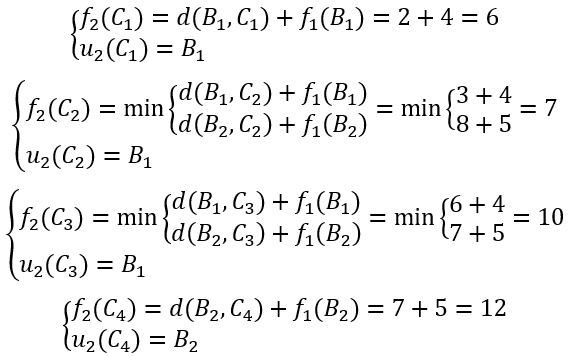
类似地，可算得

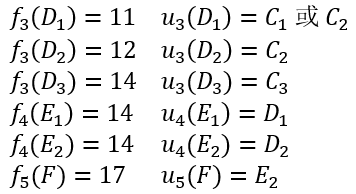
按定义知 为所求最短路长，而路径则为 ，全部计算情况如图2所示。图中每节点上方括号内的数表示该点到A点的最短距离，粗黑线表示该点到A点的路径。

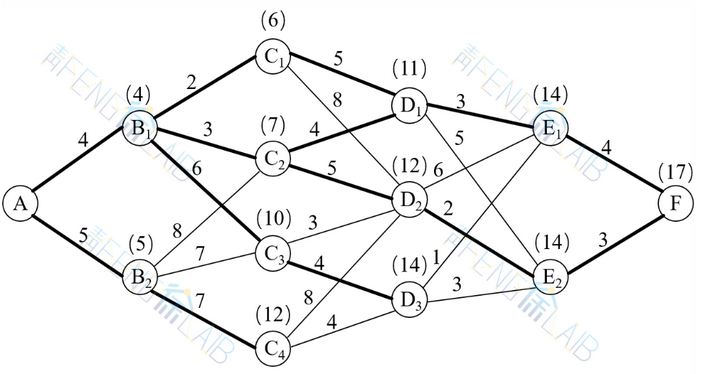
图2

上述解法可以写成如下的递推方程：

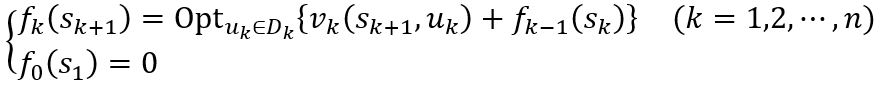
状态转移方程为：

顺序解法与逆序解法本质上并无区别，一般来说，当初始状态给定时可用逆序解法，当终止状态给定时可用顺序解法。若问题给定了一个初始状态与一个终止状态，则两种方法均可使用，如例2。但若初始状态虽已给定，终点状态有多个，需比较到达不同终点状态的各个路径及最优指标函数值，以选取总效益最佳的终点状态时，使用顺序解法比较简便。

总之，针对问题的不同特点，灵活地选用这两种方法之一，可以使求解过程简化。

二 建模注意事项

1. 状态转移方式不同

如图3所示，逆序解法中第k段的输入状态为 ，决策为 ，由此确定输出为，即第k+1段的状态，所以状态转移方程为 ，该式称为状态 到 的顺序转移方程。

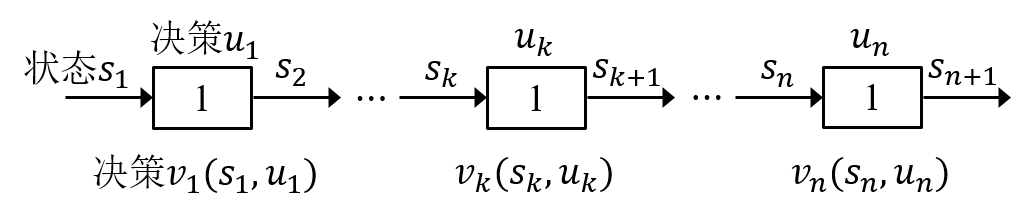
图3

顺序解法中第k段的输入状态为，决策为 ，输出为 ，如图4所示，此时的状态转移方程为 ，该式称为由状态 到 的逆序状态转移方程。

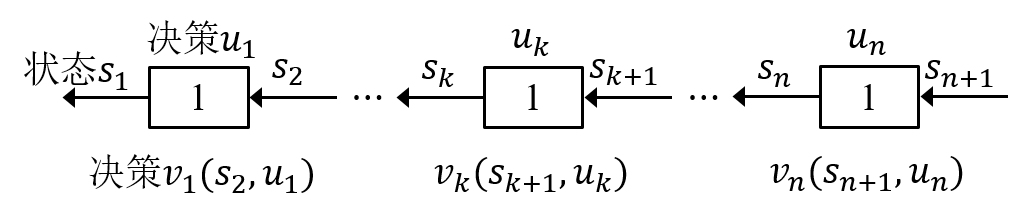
图4

同样的道理，逆序解法中的阶段指标在顺序解法中应为。

2.指标函数的定义不同

逆序解法中，我们定义最优指标函数表示第k段从状态出发，到终点后部分子过程最优效益值， 是整体最优函数值。

顺序解法中，应定义最优指标函数表示第k段从起点到状态 的前部子过程最优效益值，是整体最优函数值。

3.基本方程形式不同

（1）当指标函数为阶段指标和形式，在逆序解法中

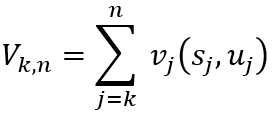
则基本方程为

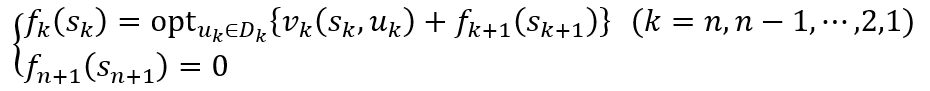
顺序解法中

基本方程为

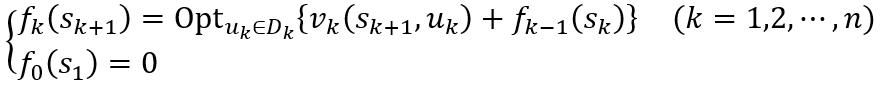
（2）当指标函数为阶段指标积形式，在逆序解法中

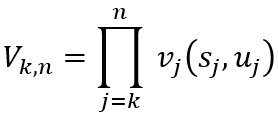
则基本方程为

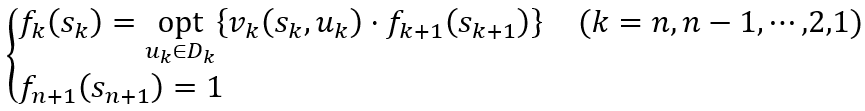
在顺序解法中，

基本方程为

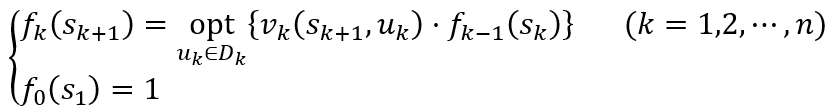
特别指出的是，这里有关顺序解法的表达式，是在原状态变量符号不变条件下得出的，若将状态变量记法改为 ，则最优指标函数也可表示为，即符号等同于逆序解法，但含义不同。

基本方程分段求解时的几种常用算法

动态规划模型建立后，对基本方程分段求解，不像线性规划或非线性规划那样有固定的解法，必须根据具体问题的特点，结合数学技巧灵活求解，大体有以下几种方法。

一 离散变量的分段穷举算法

动态规划模型中的状态变量与决策变量若被限定只能取离散值，则可采用分段穷举法。如例2的求解方法就是分段穷举算法，由于每段的状态变量和决策变量离散取值个数较少，所以动态规划的穷举法要比一般的穷举法有效。用分段穷举法求最优指标函数值时，最重要的是正确确定每段状态变量取值范围和允许决策集合的范围。

二 连续变量的解法

当动态规划模型中状态变量与决策变量为连续变量，就要根据方程的具体情况灵活选取求解方法，如经典解析方法、线性规划方法、非线性规划法或其他数值计算方法等。如在例1中，状态变量与决策变量均可取连续值而不是离散值，所以每阶段求优时不能用穷举方法处理。下面分别用逆序解法和顺序解法来求解例1。

（1）用逆序解法

由前面分析可知，例1为三段决策问题，状态变量 为第k段初拥有的可以分配给第k到第3个项目的资金；决策变量 为决定投给第k个项目的资金；状态转移方程为 ；最优指标函数 表示第k阶段，初始状态为 时，从第k到第3个项目所获最大收益，) 即为所求的总收益。递推方程为

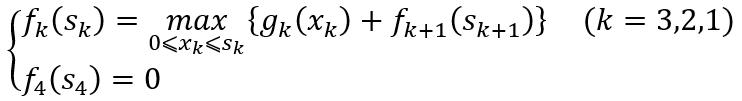
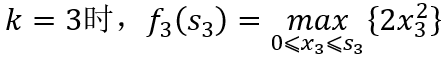
这是一个简单的函数求极值问题，易知当 时，取得极大值，即

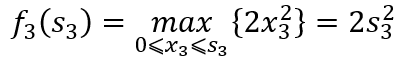
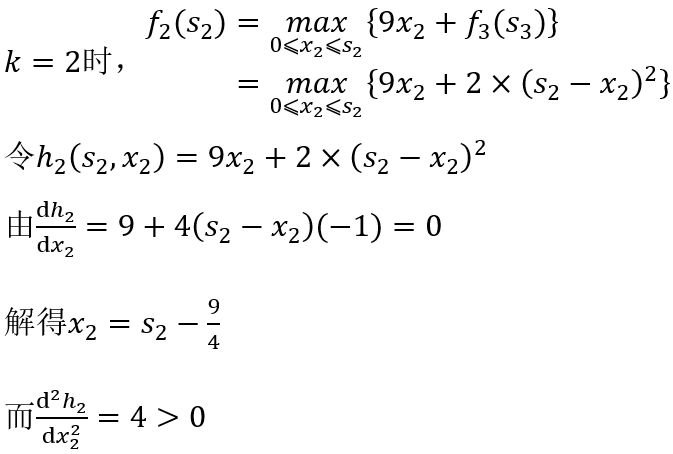
所以是极小点。

极大值只可能在 端点取得，

当 时，解得 。

当 时， ，此时

时，，此时

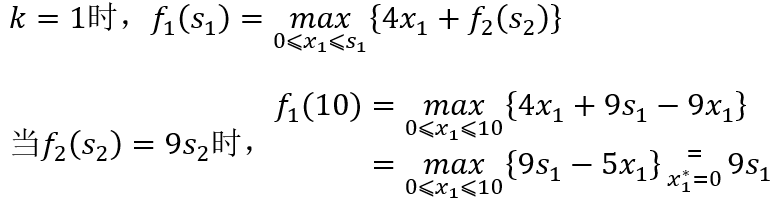
但此时

与 矛盾，所以舍去。

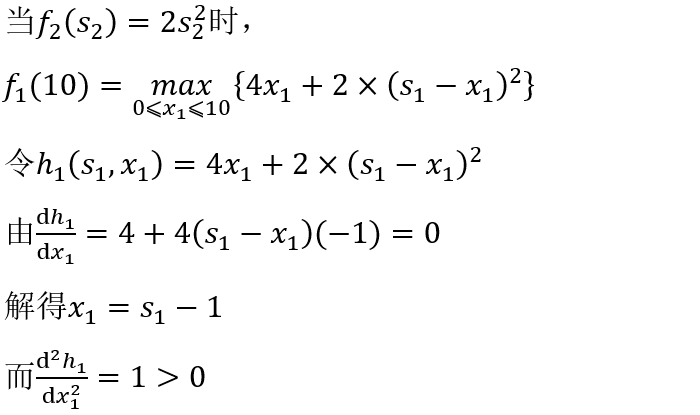
所以 是极小点。

比较[0,10]两个端点， 时，

时，

所以

再由状态转移方程顺推

因为

所以

由此

最优投资方案为全部投资于第3个项目，可得最大收益200万元。

（2）用顺序解法

阶段划分和决策变量的设置同逆序解法，令状态变量表示可用于第1到第k个项目投资的金额，则有状态转移方程为

令最优指标函数 表示第k段投资额为时第1到第k项目所获的最大收益，此时顺序解法的基本方程为

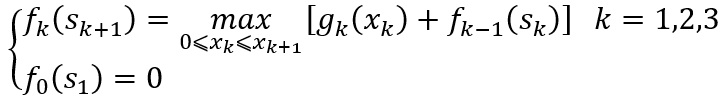
当k=1时，有

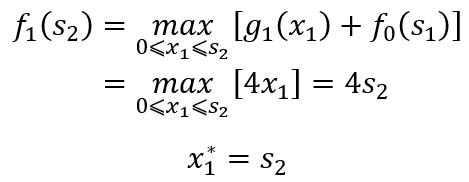
当k=2时，有

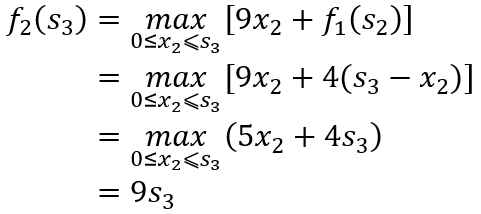
当k=3时，有

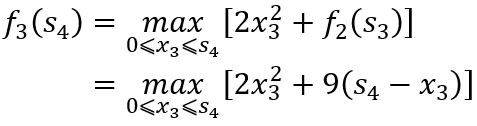
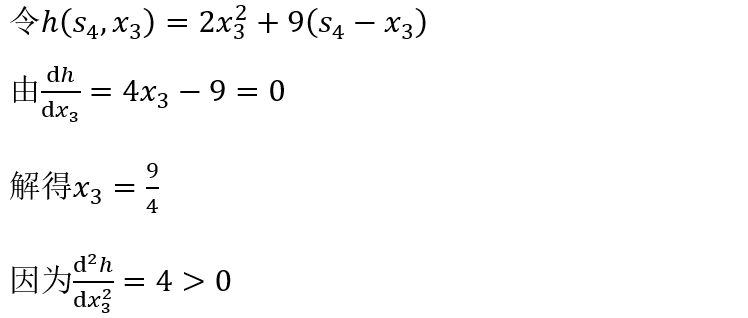
所以，此点为极小点。

极大值应在端点 取得

当 时，，

当 时， ，

所以

再由状态转移方程逆推：

所以最优投资方案与逆序解法结果相同，只投资于项目3，最大收益为200万元。比较两种解法的过程，可以发现，对本题而言，顺序解法比逆序解法简单。

三 连续变量的离散化解法

接下来，小编还是利用投资分配问题先介绍连续变量离散化的概念，如投资分配问题的一般静态模型为：

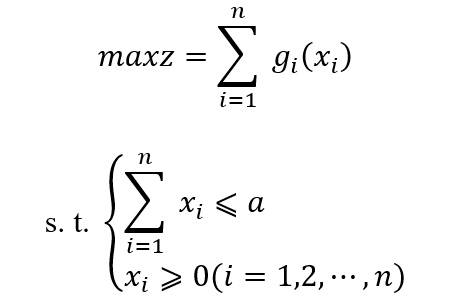
建立它的动态规划模型，其基本方程为

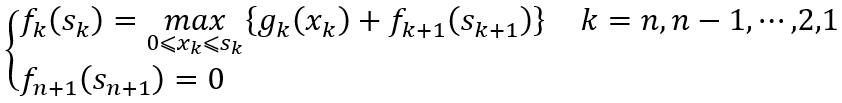
其状态转移方程为

由于 与 都是连续变量，当各阶段指标 没有特殊性质而较为复杂时，要求出 会比较困难，因而求全过程的最优策略也就相当不容易，这时常常采用把连续变量离散化的办法求解其数值解，具体做法如下：

（1）令 ，把区间 进行分割， Δ 的大小可依据问题所要求的精度以及计算机的容量来定。

（2）规定状态变量以及决策变量 只在离散点上取值，相应的指标函数 就被定义在这些离散值上，于是递推方程就变为

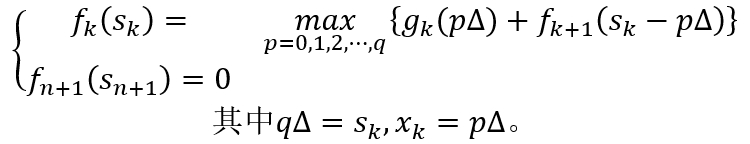
（3）按逆序方法，逐步递推求出 ，最后求出最优资金分配方案。

小编仍使用例1作为离散化例子

解：规定状态变量和决策变量只在给出的离散点上取值，令 Δ=2 ，将区间[0,10]分割0,2,4,6,8,10成六个点，即状态变量集合为{0,2,4,6,8,10}。

允许决策集合为， 与 均在分割点上取值。

动态规划基本方程为

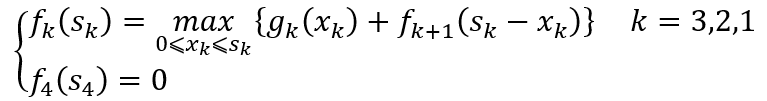
当k=3时，

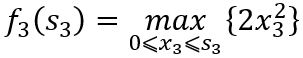
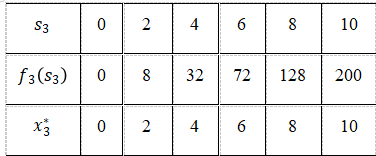
式中 和 的集合均为{0,2,4,6,8,10}。计算结果见表1。

表1

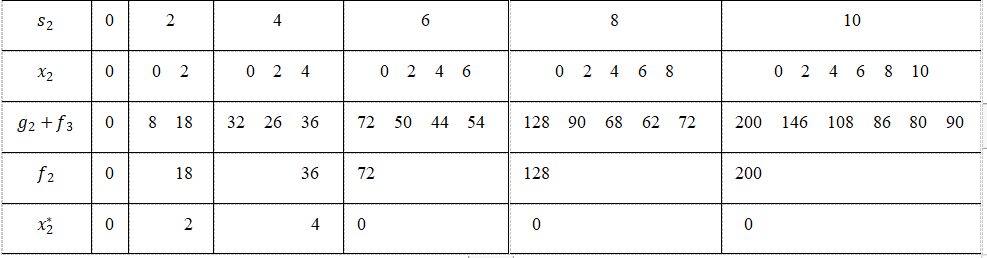
当k=2时，

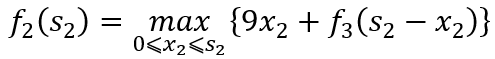
计算结果见表2

表2

当k=1时，

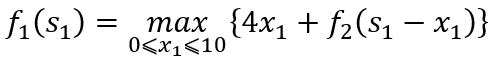
计算结果见表3

表3

???????

计算结果表明，最优决策为： ，最大收益为 ，与上述用逆序和顺序算法得到的结论完全相同。

应指出的是，这种方法有可能丢失最优解，一般得到原问题的近似解。

作者 | 张宇 刘智厅

责编 | 刘文志

审核 | 徐小峰