算法(图网格)-岛屿问题-岛屿数量
发布时间:2023年12月26日
岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
Related Topics
深度优先搜索
广度优先搜索
并查集
数组
矩阵
Java实现代码如下
package algorithm.array;
import org.junit.Test;
/**
* numIslands
*
* @author allens
* @date 2023/12/25
*/
public class NumIslands {
public int numIslands(char[][] grid) {
boolean flag = true;
int count = 0;
while (flag) {
boolean has = false;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == '1') {
has = true;
flag = recursive(grid, j, i);
if (flag) count ++;
}
}
}
if (!has) break;
}
return count;
}
public boolean recursive (char[][] grid, int x, int y) {
if (y >= grid.length || y < 0) return false;
if (x >= grid[0].length || x < 0) return false;
// 如果这个格子不是岛屿,直接返回
if (grid[y][x] != '1') {
return false;
}
grid[y][x] = '2'; // 将格子标记为「已遍历过」
// 上
recursive(grid, x, y - 1);
// 下
recursive(grid, x, y + 1);
// 左
recursive(grid, x - 1, y);
// 右
recursive(grid, x + 1, y);
return true;
}
@Test
public void testMain () {
int result = numIslands(new char[][]{
{'1', '1', '1', '1', '0'},
{'1', '1', '0', '1', '0'},
{'1', '1', '0', '0', '0'},
{'0', '0', '1', '0', '1'}
});
}
}
网格遍历:
每一个格子都会往上下左右方向移动,但网格是有边界的,移动到边界之后要停止移动,同时移动到已经处理过后的格子的时候也停止移动。
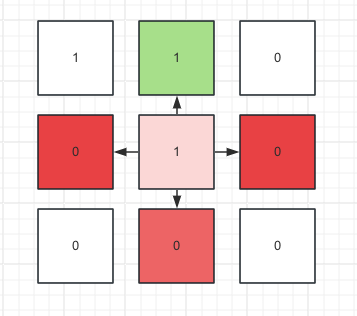
比如grid[1][1]这个节点上下左右需要处理的逻辑。向上发现值为1可以继续处理,向左发现为0直接停止移动,向右向下同理。
public boolean recursive (char[][] grid, int x, int y) {
if (y >= grid.length || y < 0) return false;
if (x >= grid[0].length || x < 0) return false;
// 如果这个格子不是岛屿,直接返回
if (grid[y][x] != '1') {
return false;
}
grid[y][x] = '2'; // 将格子标记为「标记已遍历过」,如果没有这段会导致无限循环
// 上
recursive(grid, x, y - 1);
// 下
recursive(grid, x, y + 1);
// 左
recursive(grid, x - 1, y);
// 右
recursive(grid, x + 1, y);
return true; // 只要代码能进到这段就说明有小岛,直接返回true
}
文章来源:https://blog.csdn.net/yh4494/article/details/135226291
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 网络安全(黑客)—2024自学
- [蓝桥 2023] 位乘积计数
- ModuleNotFoundError: No module named ‘sklearn.cross_validation‘
- 12.27重构二叉树,插入排序,队列(股票,模拟),后缀表达式求值,括号匹配,验证栈序列,选择题部分
- 一文搞懂 Python 文件读写操作
- 深度学习算法应用实战 | DINOv2 图像相似度实战
- IDEA创建导入Maven工程时出错Connection refused to host
- 性能篇:LinkedList循环为什么使用Iterator而不是for?
- 代码随想录算法训练营第六天 | 242. 有效的字母异位词、349. 两个数组的交集、202. 快乐数、1. 两数之和
- 全网最详细的vue2引入svg详细步骤