C/C++ BM2链表内指定区间反转
发布时间:2023年12月26日
前言
这题是BM1的升级版,不过是把完整的链表翻转变成了指定区间。
题目

描述
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转,要求时间复杂度 O(n),空间复杂度 O(1)。
例如:
给出的链表为 1→2→3→4→5→NULL
返回 1→4→3→2→5→NULL
数据范围: 链表长度 0<size≤10000<size≤1000,0<m≤n≤size0<m≤n≤size,链表中每个节点的值满足 ∣val∣≤1000
要求:时间复杂度 O(n) ,空间复杂度 O(n)
进阶:时间复杂度 O(n),空间复杂度 O(1)
示例1
输入:
{1,2,3,4,5},2,4
返回值:
{1,4,3,2,5}
示例2
输入:
{5},1,1
返回值:
{5}
1. 解决方案一
1.1 思路阐述
做完BM1,再做BM2,第一反应就是套用BM1的代码。
这里套用BM1的思路2。
BM1是全局翻转,所以只要从第一个节点开始反转即可;
BM2是区间翻转,因此要找到区间的起始节点,即第m个节点开始的子链表,再把区间m到n的节点翻转,再拼凑前后端链表即可。
代码具体思路如下
- 添加表头,定义前序节点;
- 找到第m个节点的前一个节点。
这里找前一个节点而不是直接定位到第m个节点,因为后续取子链表的时候,如果是m节点,会出现节点个数少1的情况。比如输入{5,3},1,2。在分离前链表的时候,由于pre指向的是m的位置,也就是5,如果把5的后面节点置为空节点,那么相当于倒置的是m后面的节点m1到n的子链表。但是对于我们自定义的这个输入,pre其实应该指向的是头结点-1的位置,头结点后的5,3才是我们要倒置的链表。 - 找到第n个节点的位置;
- 取两个链表,一个是m开始的链表,一个是n后面的尾链表
- 分离子链表,把m前面的链表和m开始的链表断开;把n开始的链表和n后面的尾链表断开;
- 翻转m开始的链表(这时候m开始的链表已经是m到n区间的链表了)
- 把刚才分离的链表拼接上翻转后的链表
- 返回头结点res的下一个节点开始的链表
下面是我画的一个流程草图
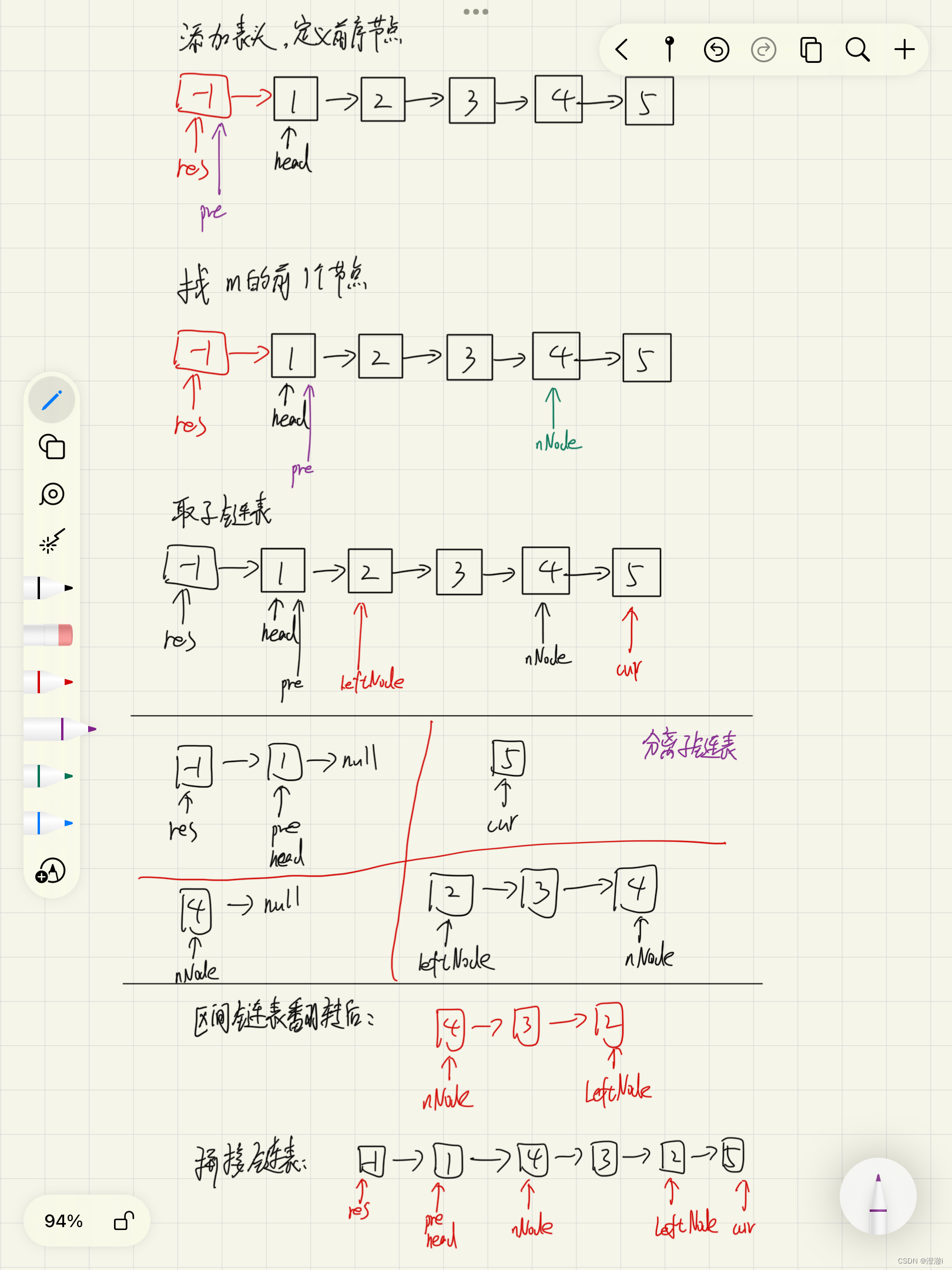
1.2 源码
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int m, int n) {
//加个表头
ListNode* res = new ListNode(-1);
res->next = head;
//前序节点
ListNode* pre = res;
//找到m的前一个节点
for(int i = 1; i < m; i++){
pre=pre->next;
}
//找到n
ListNode *nNode=pre;
for(int i = 0; i < n-m+1; i++){
nNode=nNode->next;
}
//取子链表
ListNode *LeftNode=pre->next;
ListNode *cur=nNode->next;
//分离子链表
pre->next=nullptr;
nNode->next=nullptr;
//翻转区间链表
reverseLinkList(LeftNode);
//拼接链表
pre->next=nNode;
LeftNode->next=cur;
//返回去掉表头
return res->next;
}
void reverseLinkList(ListNode *head)
{
ListNode *pre = nullptr;
ListNode *cur = head;
while(cur!=nullptr){
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
}
};
2. 解决方案二
2.1 思路阐述
相比于第一种方法,这种方法就不涉及到拆分和拼接链表的过程。
方法二是断开要倒置的链表节点,将其插入到前一个节点去,其他保持不变。最主要的是要理清楚节点之间的关系。
- 添加表头,定义前序节点和当前节点
- 找到m节点的位置,作为当前节点。前序节点为cur当前节点的前一个节点。
- 因为n是始终大于m的,所以我们可以使用for循环,翻转m到n之间的节点。
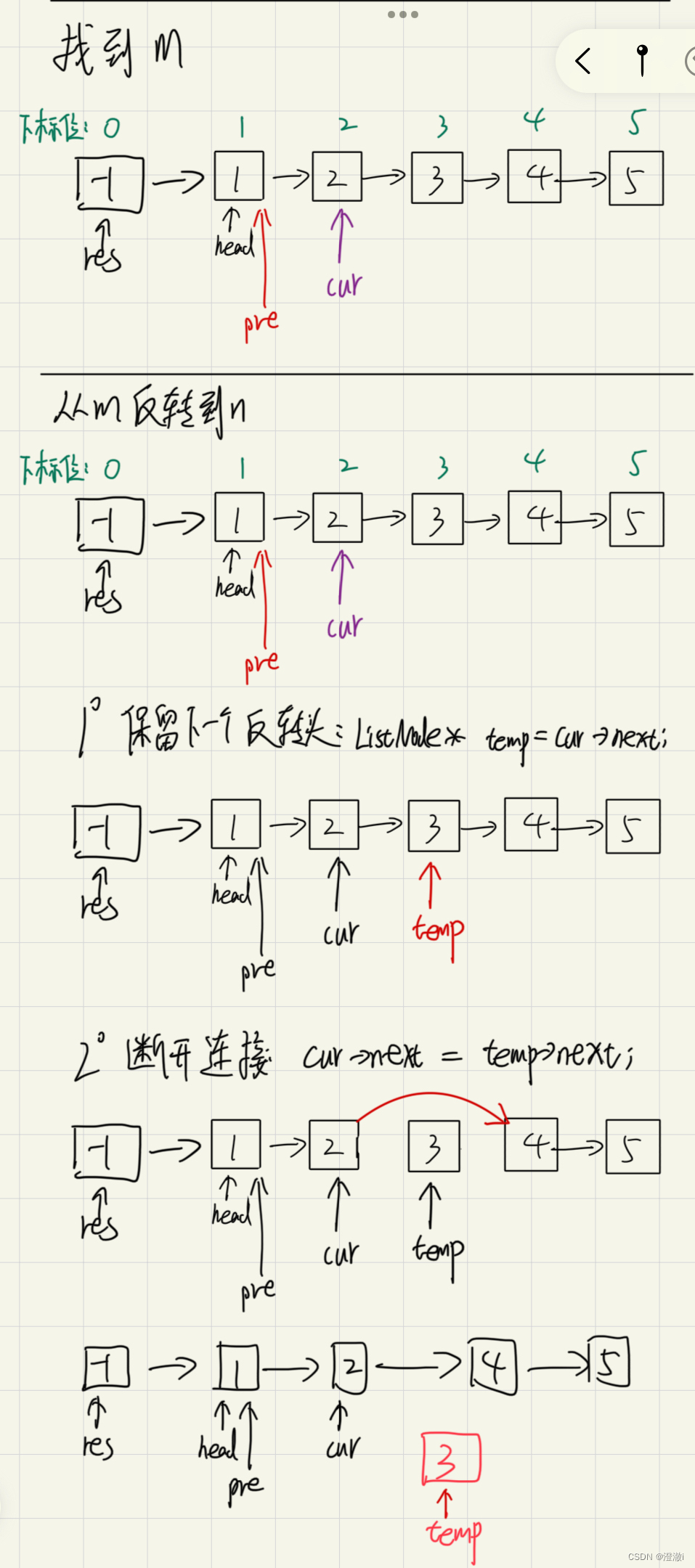
翻转过程如下
- 首先保存下一个要反转子链表表头temp
- 将当前节点cur和temp之间断开,将cur直接与反转子链表表头temp的后续节点相连,这一步就是断开cur与temp的关系,同时把temp节点独立出来。
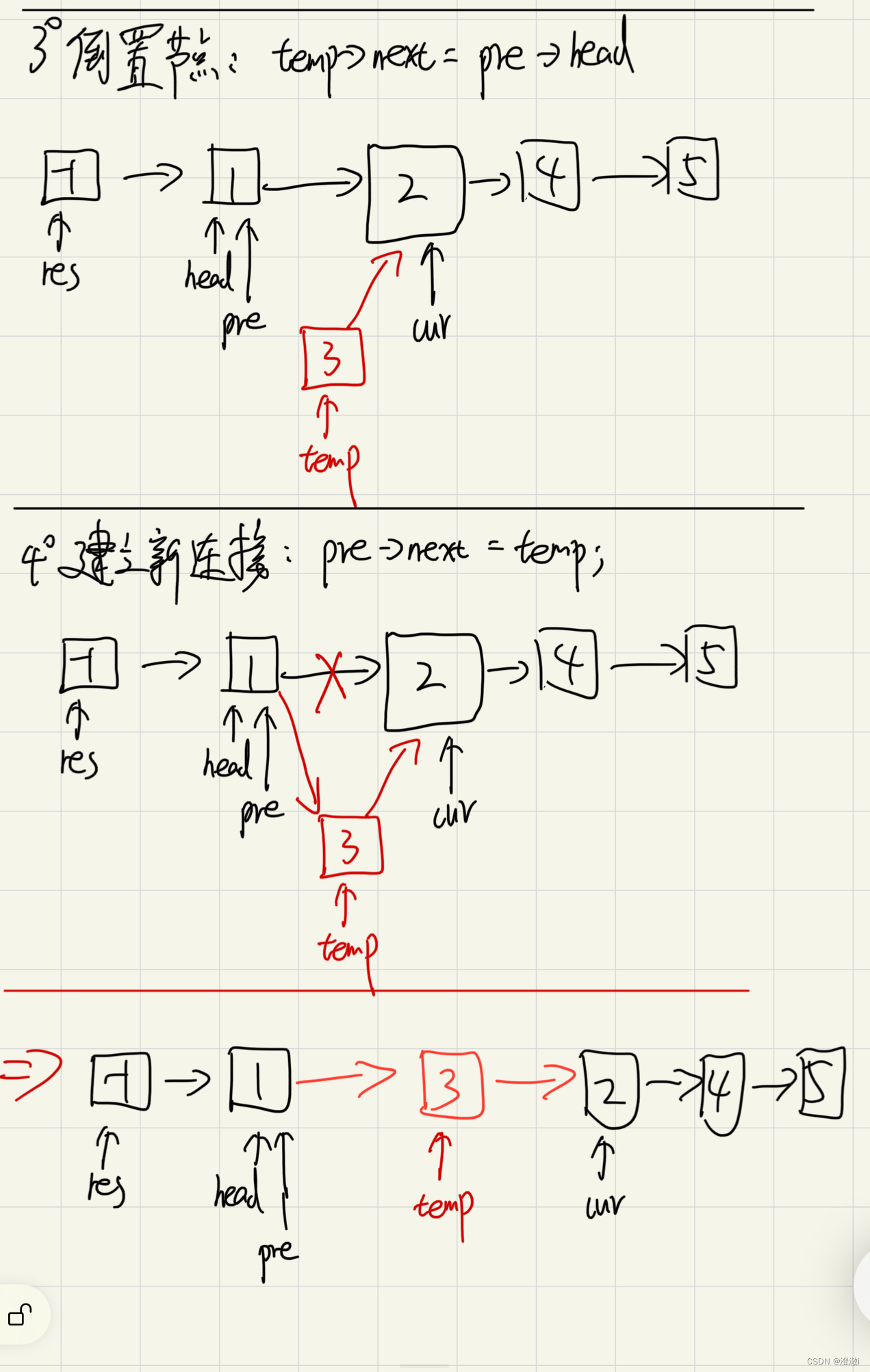
- 接下来就是一个插入节点的过程;首先就是保证原有链表顺序不发生变化,将temp的下一个节点指向当前节点cur,再将cur的前序节点的下一个节点指向temp,断开cur前序节点和cur之间的关系,并将pre作为temp的前序节点,从而完成倒置效果。
- 重复上述操作,重复次数即为m到n之间的节点个数。
- 最后是返回表头节点对应的下一个节点开始的链表。
下面是我画的草图
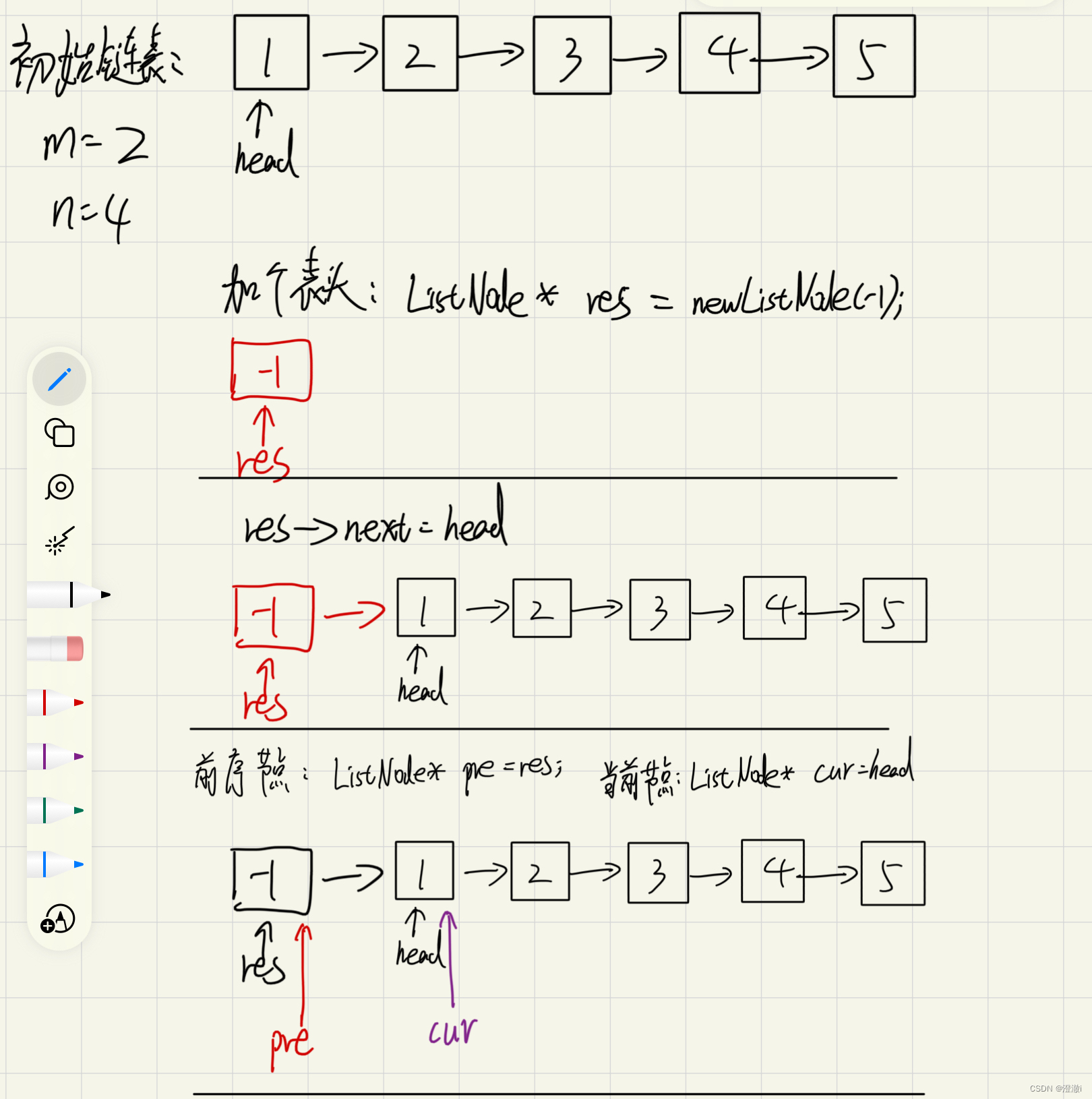
2.2 源码
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int m, int n) {
//加个表头
ListNode* res = new ListNode(-1);
res->next = head;
//前序节点
ListNode* pre = res;
//当前节点
ListNode* cur = head;
//找到m
for(int i = 1; i < m; i++){
pre = cur;
cur = cur->next;
}
//从m反转到n
for(int i = m; i < n; i++){
ListNode* temp = cur->next;
cur->next = temp->next;
temp->next = pre->next;
pre->next = temp;
}
//返回去掉表头
return res->next;
}
};
总结
这道题是结合了BM1的链表翻转,并增添了遍历指定位置节点、链表断表、插入、组合等操作。难度比上一题BM1加大,核心思想不变,依旧是倒置链表。
文章来源:https://blog.csdn.net/Edwinwzy/article/details/135202839
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【计算机毕业设计】SSM在线宿舍管理系统
- Docker部署系列之Docker Compose安装Redis三主三从集群
- RIP路由信息协议
- Linux:linux计算机和windows计算机 之间 共享资源
- 《深入理解JAVA虚拟机笔记》类加载机制
- Python数据可视化
- Multimodal Attention-based Fusion Networks for Diagnosis Prediction
- 3d可视化机房的秘密:核心原来是机房可视化动力环境监控系统!
- 华为821易错总结
- OpenGL排坑指南—贴图纹理绑定和使用