Grind75第11天 | 310.最小高度树、127.单词接龙、230.二叉搜索树中第k小的元素

310.最小高度树

题目链接：https://leetcode.com/problems/minimum-height-trees

解法：

这个题类似最短路径问题，用的BFS。

从题目的例子可以看到，最小高度树的根节点，好像是入度比较大的节点，这是一个大概的认识。

为了找到这些点，我们从边缘开始，先找到所有出度为1的节点，然后把所有出度为1的节点进队列，以它们为包围圈，不断地BFS，最后找到的就是两边同时向中间靠近的节点。

那么相比于从一端到另一端，从中间到一端的路径肯定更短。所以BFS结束后，就找到了最小高度树的根节点。

参考题解：BFS

边界条件：

时间复杂度：O(n)，其中?n?是为节点的个数

空间复杂度：O(n)，其中?n是为节点的个数

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]
        res = []
        # 记录每个点的入度
        degree = [0] * n
        # 存储邻接节点
        adjacency = defaultdict(list)
        for edge in edges:
            degree[edge[0]] += 1
            degree[edge[1]] += 1
            adjacency[edge[0]].append(edge[1])
            adjacency[edge[1]].append(edge[0])

        # 把入度为1的节点加入列表
        que = deque()
        for i in range(n):
            if degree[i] == 1:
                que.append(i)

        # 一次性遍历入度为1的节点（叶子结点），把这层叶子结点删除后新的叶子结点加入队列
        while que:
            # 每一轮都更新最小高度树
            res = []
            size = len(que)
            for i in range(size):
                cur = que.popleft()
                res.append(cur)
                neighbors = adjacency[cur]
                # cur 从队列拿出来，那就不存在了，所以相邻节点的入度减1
                for neighbor in neighbors:
                    degree[neighbor] -= 1
                    # 如果变成了叶子结点，那么加入队列
                    if degree[neighbor] == 1:
                        que.append(neighbor)
        # 最后返回的叶子节点，就是最小高度树的节点
        return res

127.单词接龙

题目链接：https://leetcode.com/problems/word-ladder

解法：

单词列表可以转化为无向图，只要一个字母不同的单词之间是相邻的。

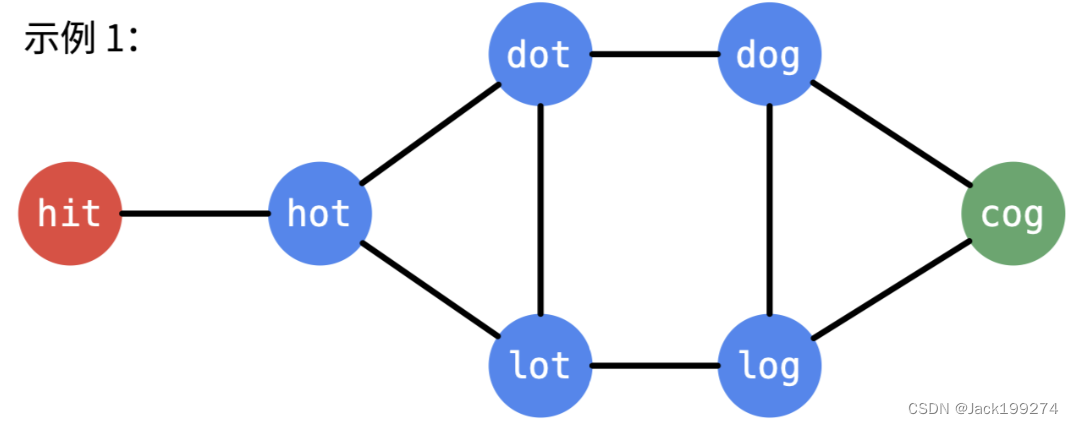
那么这个题转化为无向图中两个顶点之间的最短路径的长度，可以通过广度优先遍历得到。

参考的题解中，考虑到无向图没有直接给出，如果构建为邻接表就需要对单词进行两两比较，时间复杂度较高，于是没有构建邻接表。替换方案是：在遍历队列元素时，通过把单词的某个字符替换为26个字母中的一个，并且替换后的单词需要在word_list里面，这样的替换单词就是相邻节点。

参考题解：BFS

边界条件：

时间复杂度：

空间复杂度：

class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        word_set = set(wordList)
        if endWord not in word_set:
            return 0
        
        que = deque([beginWord])
        visited = set([beginWord])
        # 变换后的长度是一样的
        word_len = len(beginWord)
        # 每一轮遍历，那么路径加1
        step = 1
        while que:
            step += 1
            size = len(que)
            for i in range(size):
                word = que.popleft()
                word_list = list(word)
                # 对于word中的一个字符进行替换
                for j in range(word_len):
                    raw_char = word_list[j]

                    for k in range(26):
                        word_list[j] = chr(ord('a')+k)
                        # 替换一个字符后的word
                        next_word = ''.join(word_list)
                        if next_word in word_set:
                            if next_word == endWord:
                                return step
                            if next_word not in visited:
                                que.append(next_word)
                                visited.add(next_word)
                    # 还原该位置的字符，继续替换另一个位置的
                    word_list[j] = raw_char
        return 0

230.二叉搜索树中第k小的元素

题目链接：https://leetcode.com/problems/kth-smallest-element-in-a-bst

解法：

二叉搜索树具有一个重要性质：二叉搜索树的中序遍历为递增序列。

本题可被转化为求中序遍历的第?k个节点，那么我们不用遍历所有的节点，只需要在遍历过程中同时记录节点个数，个数为k时就返回节点的值。

参考题解：中序遍历

边界条件：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        self.res = 0
        # 这个k必须是全局变量，一直在减小，而不是可以回溯的，所以不能作为dfs的形参
        self.k = k
        self.dfs(root)
        return self.res
    
    def dfs(self, root):
        if not root: return
        # 处理左，一直深入到叶子节点才返回
        self.dfs(root.left)
        # 处理中，剪枝的操作
        if self.k == 0: return
        self.k -= 1
        if self.k == 0: 
            self.res = root.val
        # 处理右
        self.dfs(root.right)