条件概率、全概率和贝叶斯公式

目录

1. 条件概率

1.1 条件概率说明

1.2?举例说明

1.3?条件概率公式

2. 全概率公式

2.1 条件概率公式

2.2 一个特例公式

2.3?全概率公式的意义

3. 贝叶斯公式

3.1 贝叶斯公式的推导

3.2?贝叶斯公式一个特例

???????3.3?贝叶斯公式的意义

4. 先验概率?&?后验概率

4.1 举例

???????4.2?先验概率 & 后验概率的定义

---

---

1. 条件概率

1.1 条件概率说明

????????在一间事情已经发生的情况下，另一件事情发生的概率。

1.2?举例说明

将一枚硬币抛掷两次，观察其出现正反面的情况。设事件A表示“至少有一次出现正面”，事件B表示“两次都出现同一面”。求

? ? ? ? 1) 事件 B的概率;

? ? ? ? 2) 已知A发生的条件下，事件B的概率。

????????用H表示正面，T表示反面，样本空间如下：

????????????????S={HH,HT,TH,TT}?

????????????????A={HH,HT,TH}

????????????????B={HH,TT }

1. B的概率是： ?
2. 若已知事件A己发生，则A的基本事件只有三个:HH,HT,TH，样本空间缩小，其中有利于B的基本事件只有一个:HH。因此，已知A发生的条件下，事件B发生的概率为 ?

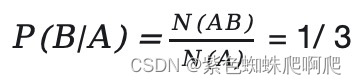
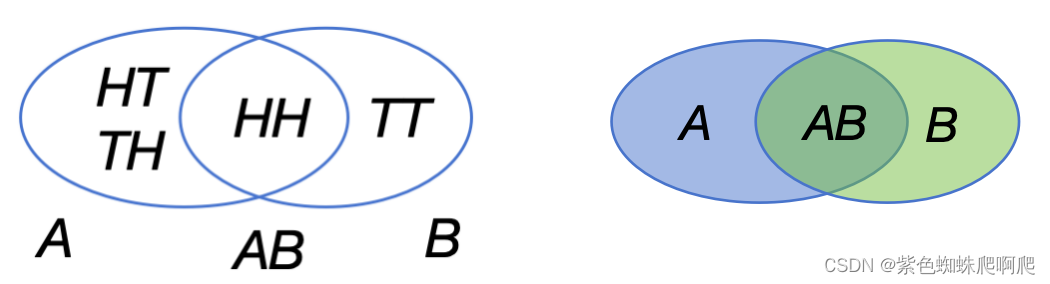
P(B|A)叫做A发生的条件下B发生的概率，所以这个就叫做条件概率。可以理解为B中样本点在A中所占的比例，也是AB中的基本事件在A中所占的比例。

1.3?条件概率公式

• 设随机事件的基本事件总数N(S)
• 事件A包含的基本事件为N(A)>0
• 事件AB包含的基本事件为N(AB)

则根据古典概型的概率计算公式，在已知事件A发生的条件下，事件B发生的概率为：

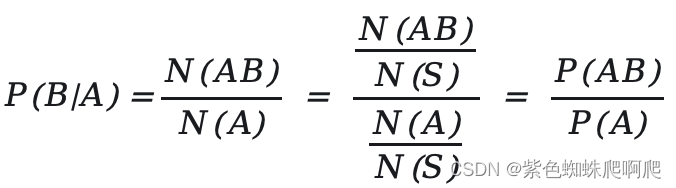
转化为乘法公式为：

2. 全概率公式

2.1 条件概率公式

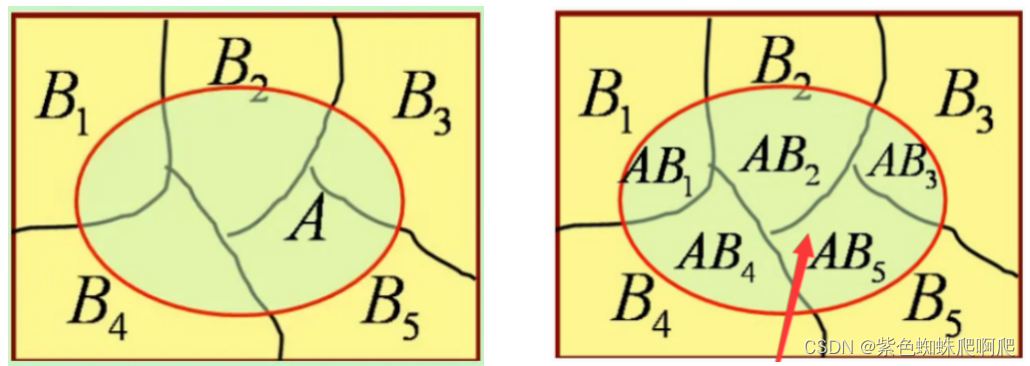
事件?B1,B2,...Bn?构成实验E的完备事件组，即它们两两不相容，和为全集。且?P(Bi)>0?，A为E的一个事件。则：

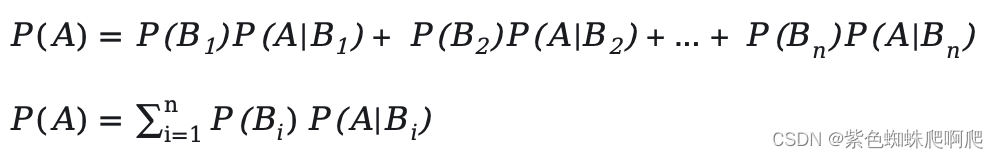
2.2 一个特例公式

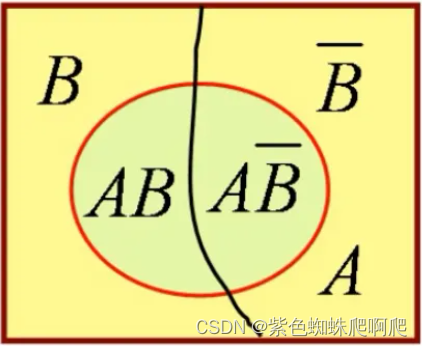
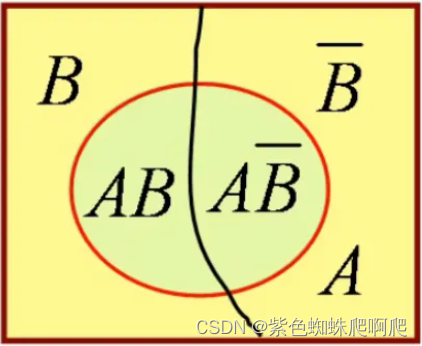
当B只有两个事件时，B和非B。公式变为：

记住这个特例公式，在将来的二分类Logistics回归可以用到。

2.3?全概率公式的意义

事件A的发生有各种可能的原因Bi(i=1,…..,n)。如果A是由原因Bi引起，则A发生的概率为P(ABi)?= P(B)P(A|Bi)

每一个原因都可能导致A发生，故A发生的概率是全部原因引起A发生的概率的总和，即为全概率公式。

由此可以形象的把全概率公式看成是“由原因推结果”的公式。每个原因对结果的发生有一定的作用，结果发生的可能行与各种原因的作用大小有关，全概率公式就表达了他们之间的关系。

3. 贝叶斯公式

3.1 贝叶斯公式的推导

由条件概率出发，分子通过一步条件概率变形，分母通过全概率公式变形。重点：不必分子分母同时变形，只变其中之一也行。

???????3.2?贝叶斯公式一个特例

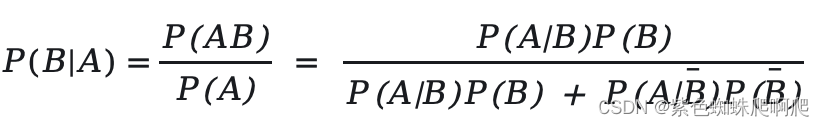
???????3.3?贝叶斯公式的意义

在事件A已经发生的条件下，贝叶斯公式可以用来寻找导致A发生的各种原因Bi的概率。

可以看出，贝叶斯公式是“由果溯因”的思想，当知道某件事的结果后，由结果推断这件事是由各个原因导致的概率为多少。

4. 先验概率?&?后验概率

4.1 举例

设机器调整得良好时，产品的合格率为95%，而当机器发生某种故障时，其合格率为50%。设机器调整良好的概率为90%。已知某日生产的第一件产品是合格品，求机器调整良好的概率。

用A表示“产品合格”，B表示“机器调整良好”：

已知：P(B)=0.9 -> P()=0.1

P(A|B)=0.95

P(A|)=0.5

在A发生的情况下，求B的概率就是P(B|A)

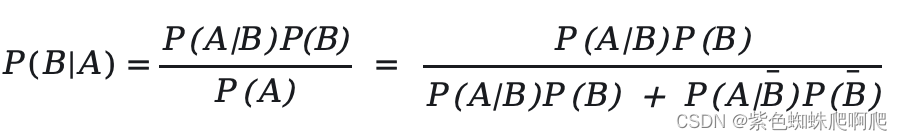
P(B|A)≈0.945

P(B|A)≠P(B)

机器调整良好的概率P(B)=0.9是由以往的数据分析所得，称为先验概率。

而条件概率P(BIA)≈0.945是在得到产品合格的信息之后再重新加以修正的概率，称为后验概率。

有了后验概率，我们就能对机器的调整状态有进一步的了解。

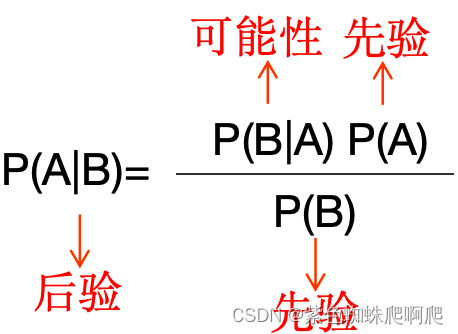
???????4.2?先验概率 & 后验概率的定义

• 先验概率（prior probability）：指根据以往经验和分析。在实验或采样前就可以得到的概率。
• 后验概率（posterior probability）：指某件事已经发生，想要计算这件事发生的原因是由某个因素引起的概率。

可以看出，先验概率就是事先可估计的概率分布，而后验概率类似贝叶斯公式“由果溯因”的思想。

参考文档：

条件概率：条件概率 - 知乎

全概率和贝叶斯：全概率公式、贝叶斯公式 - 知乎

先验、后验概率：<基础系列>1：先验概率 & 后验概率 - 知乎