参数曲线之幂基曲线

在 CAD（计算机辅助设计）软件中，幂基曲线常常被用于创建和修改几何对象。通过交互式操作，用户可以调整曲线的系数，从而改变曲线的形状。这种方法使得用户可以直观地修改曲线，而不需要深入了解曲线的数学表达式。

一条n次曲线的幂基表示形式是：

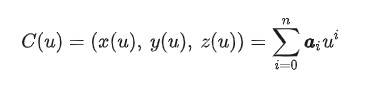
其中

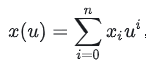
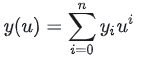
给定u0，计算幂基曲线上的点C(u0)的最有效算法是英国数学家W.G.Horner提出的Horner方法。Horner算法是递归概念的一个典型实例，它采用最少的乘法来进行多项式求值，使计算由X^n问题转化为O（n）的问题。

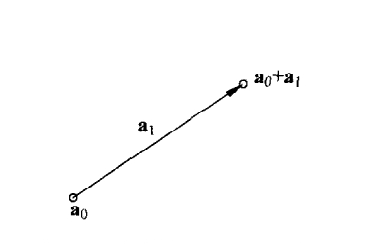
?当次数＝1时：

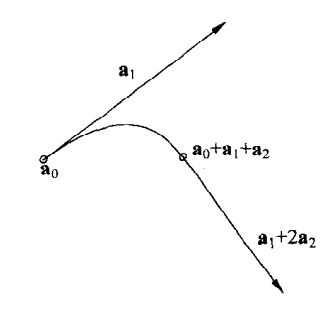
?当次数＝2时：

?……

当次数＝n时：

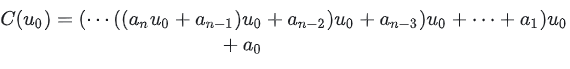
void Horner1(a, n, u0, C) 
{
  C = a[n]; 
  for (int i = n-1; i >= 0; i--) 
  { 
    C = C * u0 + a[i]; 
  } 
}

#include<iostream>
typedef double Standard_Real; 
typedef int Standard_Integer; 
void  NoDerivativeEvalPolynomial(const Standard_Real Par, 
const Standard_Integer Degree, 
const Standard_Integer Dimension,  
const Standard_Integer DegreeDimension,  
Standard_Real&         PolynomialCoeff, 
Standard_Real&         Results) 
{ 
    Standard_Integer jj; 
    Standard_Real *RA = &Results ;   
    Standard_Real *PA = &PolynomialCoeff ; 
    Standard_Real *tmpRA = RA; 
    Standard_Real *tmpPA = PA + DegreeDimension; 
    switch (Dimension) { 
        case 1 : 
        { 
            *tmpRA = *tmpPA; 
            for (jj = Degree  ; jj >  0 ; jj--) 
            { 
                tmpPA--; 
                *tmpRA = Par * (*tmpRA) + (*tmpPA); 
                } 
                break; 
        } 
    }
} 
int main() 
{
    Standard_Real Par = 2.0;
    Standard_Integer Degree = 3-1;
    Standard_Integer Dimension = 1;
    Standard_Integer DegreeDimension = 2;
    Standard_Real fp[3] = {1,1,1};
    Standard_Real points = 1.0;
    // 将数组首地址传入函数
    Standard_Real* PolynomialCoeff = &fp[0];
    Standard_Real* Results=&points;
?
    NoDerivativeEvalPolynomial(Par, Degree, Dimension, DegreeDimension, *PolynomialCoeff, *Results);
?
    std::cout << "Test passed!" << std::endl<<*Results<< std::endl;
    //system("pause");
    return 0;
}
?

$g++ -o main *.cpp
$main
Test passed!
7

此代码通过在线编译器测试，网址为：

https://www.cainiaojc.com/tool/cpp/

幂基曲线表示的缺点

1、幂基曲线表示用于形状设计时，不够自然，系数只能呢个传递很少的关于曲线形状的直观几何影响。

2、在数值计算时，如果幂基曲线表示的阶数太大，Horner算法易受到舍入误差的影响。