【论文笔记】Gaussian Splatting SLAM
原文链接:https://arxiv.org/abs/2312.06741
1. 引言
许多SLAM方法组合了多种3D表达;使用统一表达进行系统的所有操作(细节的局部表达、大规模几何建图和通过直接对齐进行相机跟踪)是一种有趣的进展。
本文提出第一个基于3D高斯溅射(3DGS)的在线视觉SLAM系统。3DGS中的3D场景会被表达为大量的有方向、伸长率、颜色和不透明度的高斯。其余视觉SLAM方法使用占用/有符号距离函数(SDF)体素网格、网孔、点/surfel clouds、神经场,但均有缺点:网格占用大量空间、分辨率有限;网孔需要困难无规则的拓扑以融合新信息;surfel clouds不连续,融合和优化困难;神经场需要逐像素的射线投射渲染。而本文的3DGS不含上述缺点。与点/surfel clouds类似,该方法效率高、有局部性,且容易修改。此外,可以以光滑可微的方式表达几何:一组高斯云联合定义连续体积函数,且可以使用GPU通过“溅射”栅格化来快速渲染。
本文在3DGS用于离线系统的基础上,提出改进以使其适配在线SLAM。首先推导解析的相机姿态雅可比矩阵,使得相机姿态可以和场景几何一起优化;然后引入新高斯形状正则化,以保证几何一致性,这对增量重建非常重要。还提出高斯资源分配和剪枝方法,能促进精确的相机跟踪。本文方法仅需要单目相机输入,也可以和深度测量结合使用。
2. 相关工作
密集SLAM:稀疏SLAM关注姿态估计,并生成主要用于定位的地图,而密集SLAM关注带细节的3D地图。密集SLAM可分为以帧为中心的方法和以地图为中心的方法。以帧为中心的SLAM最小化连续帧之间的光度损失,联合估计各帧深度和帧与帧之间的相机运动。这类方法因单帧对应局部几何而高效,但若需要全局地图,则需将各部分组装,但各部分之间可能没有一致性。以地图为中心的SLAM则使用统一的3D表达(通常为点或体素网格),利用全局信息进行跟踪。
体素可以进行快速3D特征查询,但占用空间且分辨率不灵活。点表达则可以自适应改变分辨率,但优化困难。基于神经网络的表达需要大量的计算来渲染,难以实时运行。
3. 方法
3.1 高斯溅射
本文的SLAM使用3DGS表达,将场景映射为一组各向异性高斯
G
\mathcal{G}
G。每个高斯
G
i
\mathcal{G}^i
Gi包含了视觉特征:颜色KaTeX parse error: Expected group after '^' at position 2: c^?和不透明度
α
i
\alpha^i
αi。对连续3D表达,均值
μ
W
i
\mu^i_W
μWi?和协方差
Σ
W
i
\Sigma^i_W
ΣWi?作为高斯在世界坐标系下的位置和椭球形状。本文省略了表达视角相关辐射的球面谐波以加快速度。通过溅射和混合
N
\mathcal{N}
N个高斯,像素颜色
C
p
\mathcal{C}_p
Cp?可按下式合成:
C
p
=
∑
i
∈
N
c
i
α
i
∏
j
=
1
i
?
1
(
1
?
α
j
)
\mathcal{C}_p=\sum_{i\in \mathcal{N}}c_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j)
Cp?=i∈N∑?ci?αi?j=1∏i?1?(1?αj?)
3DGS使用栅格化迭代高斯,不沿射线采样,从而忽略空的空间。通过溅射3D高斯
N
(
μ
W
,
Σ
W
)
\mathcal{N}(\mu_W,\Sigma_W)
N(μW?,ΣW?)形成2D高斯
N
(
μ
I
,
Σ
I
)
\mathcal{N}(\mu_I,\Sigma_I)
N(μI?,ΣI?):
μ
I
=
π
(
T
C
W
?
μ
W
)
,
Σ
I
=
J
W
Σ
W
W
T
J
T
\mu_I=\pi(T_{CW}\cdot\mu_W),\Sigma_I=JW\Sigma_WW^TJ^T
μI?=π(TCW??μW?),ΣI?=JWΣW?WTJT
其中 π \pi π为投影操作, T C W ∈ S E ( 3 ) T_{CW}\in SE(3) TCW?∈SE(3)为相机姿态, J J J为投影变换线性近似的雅可比矩阵, W W W为 T C W T_{CW} TCW?的旋转分量。这使得3D高斯可微,且混合操作能为高斯提供梯度。使用一阶梯度下降,可以细化视觉参数和几何参数来精确表达场景。
3.2 相机姿态优化
为减小自动梯度计算的开销,本文针对3DGS,提出 S E ( 3 ) SE(3) SE(3)相机姿态的解析雅可比矩阵。
3.3 SLAM
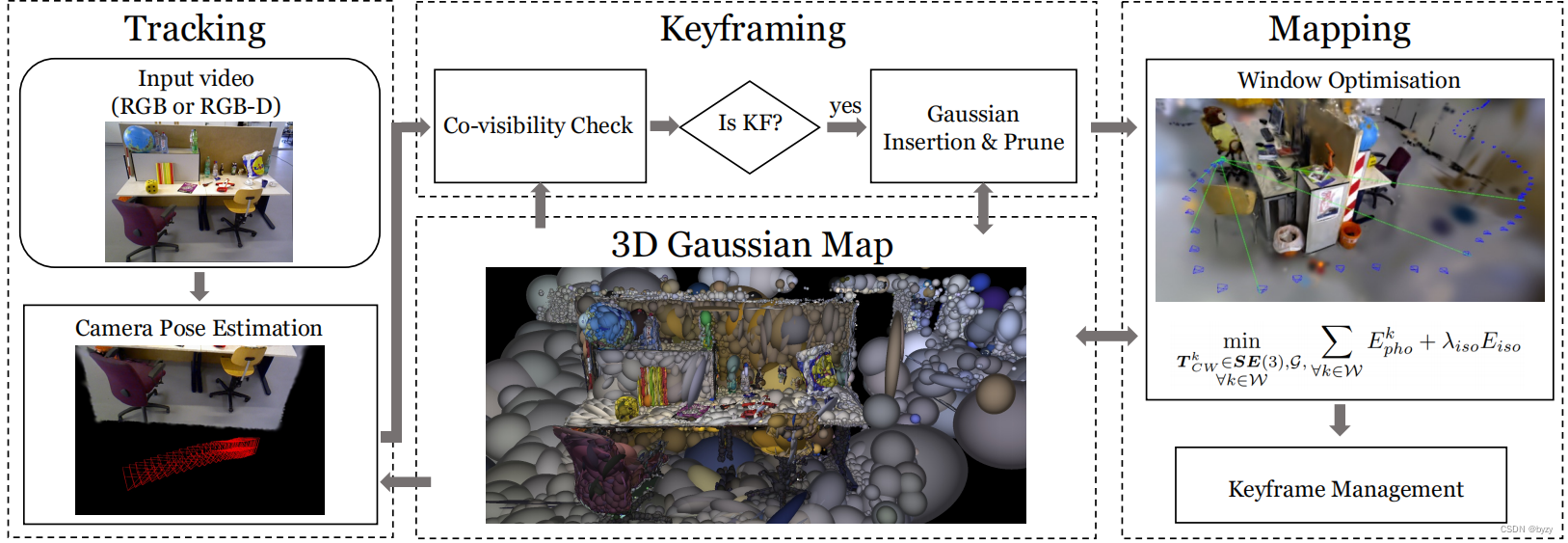
3.3.1 跟踪
跟踪时,仅优化当前帧的相机姿态,而不更新地图表达。单目情况下,最小化光度残差:
E
p
h
o
=
∥
I
(
G
,
T
C
W
)
?
I
ˉ
∥
1
E_{pho}=\|I(\mathcal{G},T_{CW})-\bar{I}\|_1
Epho?=∥I(G,TCW?)?Iˉ∥1?
其中
I
(
G
,
T
C
W
)
I(\mathcal{G},T_{CW})
I(G,TCW?)从
T
C
W
T_{CW}
TCW?渲染高斯
G
\mathcal{G}
G,
I
ˉ
\bar{I}
Iˉ为观测图像。
进一步优化不同曝光度下的仿射亮度参数。当有深度观测时,定义几何残差:
E
g
e
o
=
∥
D
(
G
,
T
C
W
)
?
D
ˉ
∥
1
E_{geo}=\|D(\mathcal{G},T_{CW})-\bar{D}\|_1
Egeo?=∥D(G,TCW?)?Dˉ∥1?
其中 D ( G , T C W ) D(\mathcal{G},T_{CW}) D(G,TCW?)从 T C W T_{CW} TCW?为深度栅格化结果, D ˉ \bar{D} Dˉ为观测图像。本文未使用深度测量初始化高斯,而是同时优化光度和几何残差。
逐像素深度通过alpha混合,按下式栅格化:
D
p
=
∑
i
∈
N
z
i
α
i
∏
j
=
1
i
?
1
(
1
?
α
j
)
\mathcal{D}_p=\sum_{i\in \mathcal{N}}z_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j)
Dp?=i∈N∑?zi?αi?j=1∏i?1?(1?αj?)
其中 z i z_i zi?为与高斯均值 μ i \mu_i μi?之间沿相机射线的距离。同样类似3.2节推导雅可比矩阵。
3.3.2 关键帧
由于使用视频中所有图像来联合在线优化高斯和相机姿态是不可行的,本文基于帧间的共视性选择关键帧。
选择和管理:检查每个跟踪帧已进行关键帧注册。通过计算当前帧 i i i和上一关键帧 j j j之间高斯的IoU来衡量共视性,当共视性低于阈值,或者相对位移 t i j t_{ij} tij?相对深度中位数很大时,将 i i i注册为关键帧。对于每个窗口 W k \mathcal{W}_k Wk?,仅遵循DSO的关键帧管理启发式方法,选择少量的关键帧。主要区别为,在与最新关键帧的重叠系数低于阈值时,移除关键帧。
高斯共视性:3DGS沿相机射线排序高斯,遵循了可视性顺序。若某高斯被用于栅格化且射线的累积 α \alpha α未到0.5,则标记该高斯为在该视图中可见。这使得估计的共视性能处理遮挡,而无需额外的启发式方法。
高斯插入与剪枝:对每个关键帧插入高斯。当存在深度测量,可通过反投影深度初始化高斯均值 μ W \mu_W μW?。单目输入下,则渲染当前帧的深度。对有深度估计的像素,在深度附近低方差初始化 μ W \mu_W μW?;对于无深度估计的像素,在深度中位数附近高方差初始化 μ W \mu_W μW?。
单目输入下,插入的高斯位置可能不正确。其中的多数会在优化中消失,因其违反了多视图一致性;本文仍通过检查高斯在当前窗口 W k \mathcal{W}_k Wk?内的可视性来剪枝。若最近3个关键帧中被插入的高斯在至少3个其余帧中未被观测到,则去除之。
3.3.3 建图
建图的目的是保留连贯的3D结构,并优化新插入的高斯。建图时,
W
k
\mathcal{W}_k
Wk?中的关键帧用于重建当前可见的区域。此外,每次迭代会有两个随机的过去窗口
W
r
\mathcal{W}_r
Wr?被选择以免遗忘全局地图。3DGS中的栅格化对沿视线方向的高斯没有约束,这在单一相机的SLAM中,会导致伪影并使跟踪困难。因此,引入各向同性正则化
E
i
s
o
=
∑
i
=
1
G
∥
s
i
?
s
~
i
?
1
∥
1
E_{iso}=\sum_{i=1}^\mathcal{G}\|s_i-\tilde{s}_i\cdot 1\|_1
Eiso?=i=1∑G?∥si??s~i??1∥1?
使用缩放因数的均值
s
~
i
\tilde{s}_i
s~i?来惩罚缩放因数
s
i
s_i
si?。这鼓励产生球形高斯,从而避免产生沿视线方向很长的高斯。设当前窗口和随机选择的过去窗口的并集为
W
=
W
k
∪
W
r
\mathcal{W}=\mathcal{W}_k\cup\mathcal{W}_r
W=Wk?∪Wr?,建图则是求解下列问题:
min
?
T
C
W
k
∈
S
E
(
3
)
,
G
,
?
k
∈
W
∑
?
k
∈
W
E
p
h
o
k
+
λ
i
s
o
E
i
s
o
\min_{T^k_{CW}\in SE(3),\mathcal{G},\forall k\in\mathcal{W}}\sum_{\forall k\in\mathcal{W}}E^k_{pho}+\lambda_{iso}E_{iso}
TCWk?∈SE(3),G,?k∈Wmin??k∈W∑?Ephok?+λiso?Eiso?
若有深度观测,也会类似3.3.1节添加几何残差项。
4. 评估
4.2 定量评估
相机跟踪精度:实验表明本文方法在单目输入下的性能比其余方案高,这表明仍然存在 通过探索SLAM表达方式 提高单目SLAM跟踪能力 的潜力。
RGB-D方法的性能与其余方法相当。本文方法在真实数据上有更高的性能,因为系统能通过优化高斯位置来灵活地处理传感器噪声。
新视图渲染:本文的方法性能排在前列,且速度快上数百倍。
消融分析:各向同性正则化和几何残差能分别提高单目与RGB-D SLAM相机跟踪的性能,因其能在光度信号弱的情况下约束几何。此外,本文遮挡感知的关键帧选择和管理能极大提高性能。与基于体素的方法相比,本文的方法需要的空间小很多;基于MLP的方法需要的空间更小,但其受限于MLP的表达能力,无法产生高保真的3D场景。
收敛盆分析:本文的SLAM实验中,相机定位有相当大的收敛盆。本文使用收敛漏斗分析,证明本文的方法比其余方法有更好的收敛性,因为各向异性高斯能形成平滑的梯度。
4.3 定性结果
可视化表明,本文的方法能处理透明物体,因为没有显示建模表面。
补充材料
7. 实施细节
7.1 系统细节和超参数
7.1.1 跟踪与建图
损失权重:有深度观测时,跟踪的损失为
min
?
T
C
W
k
∈
S
E
(
3
)
λ
p
h
o
E
p
h
o
+
(
1
?
λ
p
h
o
)
E
g
e
o
\min_{T^k_{CW}\in SE(3)}\lambda_{pho}E_{pho}+(1-\lambda_{pho})E_{geo}
TCWk?∈SE(3)min?λpho?Epho?+(1?λpho?)Egeo?
建图的损失为
min
?
T
C
W
k
∈
S
E
(
3
)
,
G
,
?
k
∈
W
∑
?
k
∈
W
(
λ
p
h
o
E
p
h
o
k
+
(
1
?
λ
p
h
o
)
E
g
e
o
k
)
+
λ
i
s
o
E
i
s
o
\min_{T^k_{CW}\in SE(3),\mathcal{G},\forall k\in\mathcal{W}}\sum_{\forall k\in\mathcal{W}}(\lambda_{pho}E^k_{pho}+(1-\lambda_{pho})E_{geo}^k)+\lambda_{iso}E_{iso}
TCWk?∈SE(3),G,?k∈Wmin??k∈W∑?(λpho?Ephok?+(1?λpho?)Egeok?)+λiso?Eiso?
7.1.2 关键帧
高斯共视性检查:使用IoU和重叠系数(OC)定义两个关键帧
i
,
j
i,j
i,j之间的共视性:
I
o
U
c
o
v
(
i
,
j
)
=
∣
G
i
v
∩
G
j
v
∣
∣
G
i
v
∪
G
j
v
∣
O
C
c
o
v
(
i
,
j
)
=
∣
G
i
v
∩
G
j
v
∣
min
?
(
∣
G
i
v
∣
,
∣
G
j
v
∣
)
IoU_{cov}(i,j)=\frac{|\mathcal{G}_i^v\cap\mathcal{G}_j^v|}{|\mathcal{G}_i^v\cup\mathcal{G}_j^v|}\\ OC_{cov}(i,j)=\frac{|\mathcal{G}_i^v\cap\mathcal{G}_j^v|}{\min(|\mathcal{G}_i^v|,|\mathcal{G}_j^v|)}
IoUcov?(i,j)=∣Giv?∪Gjv?∣∣Giv?∩Gjv?∣?OCcov?(i,j)=min(∣Giv?∣,∣Gjv?∣)∣Giv?∩Gjv?∣?
其中 G i v \mathcal{G}_i^v Giv?为在关键帧 i i i中可视的高斯。若上一关键帧为 j j j, I o U c o v ( i , j ) < k f c o v IoU_{cov}(i,j)<kf_{cov} IoUcov?(i,j)<kfcov?或相对平移 t i j > k f m D ^ i t_{ij}>kf_m\hat{D}_i tij?>kfm?D^i?(其中 D ^ i \hat{D}_i D^i?为帧 i i i的深度中位数, k f c o v kf_{cov} kfcov?和 k f m kf_m kfm?为阈值),则将关键帧 i i i加入窗口 W k \mathcal{W}_k Wk?。若 i i i为最新加入的关键帧,且 O C c o v ( i , j ) < k f c OC_{cov}(i,j)<kf_c OCcov?(i,j)<kfc?,则从窗口 W k \mathcal{W}_k Wk?中移除关键帧 j j j。
高斯插入与剪枝:插入高斯时,对于有渲染深度 D p \mathcal{D}_p Dp?的像素 p p p,从 N ( D p , 0.2 σ D ) \mathcal{N}(\mathcal{D}_p,0.2\sigma_D) N(Dp?,0.2σD?)采样深度,用于初始化高斯。对于未观测区域,从 N ( D ^ , 0.5 σ D ) \mathcal{N}(\hat{D},0.5\sigma_D) N(D^,0.5σD?)采样以初始化高斯,其中 D ^ \hat{D} D^为 D D D的中位数。对于剪枝,仅在关键帧窗口 W k \mathcal{W}_k Wk?被填满时进行基于可视性的剪枝;此外,不透明度小于0.7的高斯均会被去除。
9. 更多的消融分析
9.1 剪枝消融(单目输入)
实验表明,对随机初始化的高斯进行高斯剪枝能极大加强相机跟踪的性能,因为去掉剪枝会导致随机初始化的高斯一直存在,使得其余视图的初始几何不正确。
9.2 各向同性损失消融(RGB-D输入)
实验表明,在特定数据集上,各向同性损失能极大提高相机跟踪性能。因为栅格化没有考虑沿视线方向的伸展,各项同性正则化能阻止高斯过度伸展。
9.3 存储消耗和帧率
9.3.1 存储消耗
与原始的高斯溅射相比,本文的方法占用空间更少,因为本文通过剪枝保留约束较好的高斯,且没有储存球面谐波。
12. 局限性
本文的方法仅在房间尺度的场景下测试。对于真实世界场景,不可避免地存在轨迹偏移。可通过整合闭环模块到本文的方法中解决。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 矩阵求逆引理,SMW恒等式
- html 内外边距区别以及解释
- 文件消失但是有占用内存的恢复方法
- CSP-S 2022提高组T1:假期计划
- WebSocket
- Navicat for Redis 体验官火热招募 | 让 Redis 单机和集群管理更简单
- Linux上iPortal 配置80端口的http
- 研发日记,Matlab/Simulink避坑指南(三)——向上取整Bug
- LINUX常见问题之SYN flooding
- 【MIdjourney】几种独特的艺术风格